Iminência de Escorregamento

A figura abaixo, meramente ilustrativa (foi o melhor que eu pude fazer!) representa uma escada apoiada numa parede e as forças envolvidas.

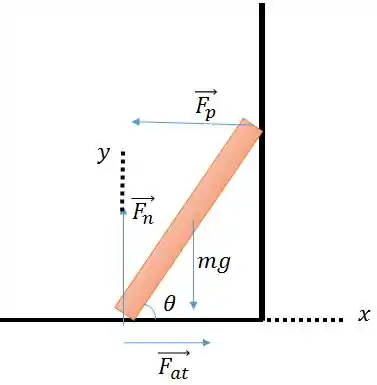
Temos a força que a parede exerce na escada

A força que o chão exerce já escada

A força de atrito

E o peso da escada .

Além disso, temos o ângulo e o coeficiente de atrito.

As questões desse tipo vão trabalhar com as relações dessas componentes.

Coeficiente de Atrito

Você já deve ter estudado, mas podemos relembrar o conceito! O coeficiente de atrito explicita a capacidade de deslizamento entre um par de superfícies.

Na situação estática crítica, ou seja, quando estamos buscando a iminência de escorregamento, ele pode ser relacionado com a força normal e com a força de atrito.

Condições de Equilíbrio

A escada está na iminência de cair, então as condições de equilíbrio valem! Você já deve ta careca de saber, mas podemos aplicar as três condições para que a escada esteja em equilíbrio:

No somatório das forças em x e y, não tem nenhum mistério. É só aplicação mesmo.

O torque também é bem parecido com o que vimos anteriormente, só precisamos ter um cuidado com a escolha do eixo de rotação.

O ângulo é descoberto por meio da decomposição das forças na equação do torque.

Eixo de Rotação

Na hora de montarmos a equação do torque, precisamos saber escolher bem seu eixo de rotação.

Essa escolha se dá de acordo com o problema. Precisamos escolher o eixo pelo qual passa a força que não temos informações.

Assim, o torque gerado por essa força será nulo e poderemos descobrir seu valor em função das outras equações.

Resolução

Após a montagem das equações, podemos resolver o problema.

O enunciado pode pedir , , para que a escada não escorregue. E aí, é só aplicar e manipular as equações da forma adequada.

Se tiver um homem subindo a escada pode ser perguntado também qual é a altura máxima que ele pode chegar.

Vamos trabalhar isso nos exercícios? Vamo que vamo