Dispersão Cromática
Produzido por Bruno SoaresTeoria
Fala aí! Bora conversar sobre Dispersão Cromática?
-Mas exatamente, o que é dispersão cromática? 😵💫
A dispersão cromática, também conhecida como dispersão óptica, é resultado do fenômeno de refração da luz. Um exemplo do nosso cotidiano é o arco-íris! 🌈🌈🌈🌈

Também vemos esse fenômeno ao passar uma luz branca através de um prisma. A luz branca é formada por todas as cores. Cada cor tem um comprimento de onda diferente, isso é, cada cor viaja com uma velocidade diferente. Isso vai afetar diretamente o índice de refração, que é dado pela seguinte fórmula:
Onde
Mas, se a luz branca é composta por várias cores e cada cor tem uma velocidade própria, logo, cada cor que compõe a luz branca vai ter um índice de refração
É ai que entra a Lei de Snell!
Onde
- Clique para saber mais:
Pra ficar mais claro, vamos olhar para o nosso prisma e pegar dois feixes de cores diferentes, a azul e a vermelha! Escolhemos essas cores porque elas estão nos extremos do espectro.
Se liga nesse esqueminha:
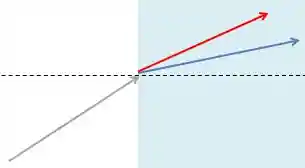
Agora podemos escrever a lei Snell para elas:
Encontrando os ângulos de refração dos extremos do espectro, é possível ver o quanto as cores se dispersam, ao entrar no vidro. Essa dispersão é a dispersão angular, e pode ser calculada subtraindo um ângulo do outro.
E sabemos que todas as cores do arco-íris irão estar dentro das faixas de ângulos entre
Como o Arco- Íris é formado?
A luz do sol incide nas gotas de água e, dentro dela, refletem algumas vezes até sair da gota.
Ao sair da gota, cada cor faz um ângulo de saída, se separando das outras e formando um fio de cores. Quando juntamos as cores que saem das várias gotas de água forma-se o arco-íris!
É assim que o arco-íris é formado!
Esse é o motivo de ser comum aparecer um arco-íris após um dia chuvoso.
Quer saber mais? Confere esse resumo em vídeo que preparamos pra você!
Agora vamos praticar com exercícios?
Como o Arco- Íris é formado?
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 33-52
Dispersão em um vidro de janela.
Na Fig.33-54 um feixe de luz branca incide com um ângulo em um vidro comum de janela (mostrado de perfil). Para esse tipo de vidro o índice de refração da luz visível varia de na extremidade azul do espectro a na extremidade vermelha.
As duas superfícies do vidro são paralelas. Determine a dispersão angular das cores do feixe:
- Quando a luz entra no vidro
- Quando a luz sai do lado oposto.
(Sugestão: Quando você olha para um objeto através de um vidro de janela as cores do objeto se dispersam como na Fig.33-20?)
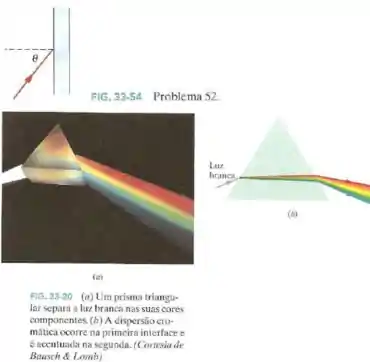
Passo 1
Letra a)
Vamos calcular o ângulo de refração para as duas cores nas extremidades do espectro visível.
Para a extremidade azul , enquanto o índice de refração do ar é e o ângulo de incidência é .
Para a extremidade vermelha .
A dispersão vai ser:
Passo 2
Letra b)
Quando a luz sair do outro lado do vidro, ela sairá paralela ao raio incidente.
De fato, tanto para o azul quanto para o vermelho teremos:
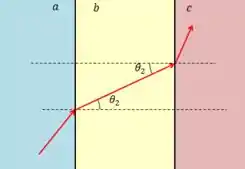
Ou seja, os ângulos incidentes e de saída serão os mesmos.
Como isso vale para todas as cores, todas elas sairão paralelas entre si e a dispersão angular vai ser zero.
Resposta
Letra a)
Letra b)
Exercício Resolvido #2
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 33-56
Arco-íris produzidos por gotas quadradas.
Suponha que, em um planeta exótico, as gotas de chuva tenham uma seção reta quadrada e caiam sempre com uma face paralela ao solo. A Fig.33-58 mostra uma dessas gostas, na qual incide um feixe de luz branca om um ângulo de incidência no ponto .
A parte da luz que penetra na gota se propaga até o ponto , onde parte é refratada de volta para o ar e a outra parte é refletida.
A luz refletida chega ao ponto , onde novamente parte da luz é refratada de volta para o ar e parte é refletida.
Qual é a diferença entre os ângulos dos raios de luz vermelha () e de luz azul () que deixam a gota:
- No ponto .
- No ponto B?
(Essa diferença faz com que um observador externo veja um arco-íris ao observar a luz que sai do ponto ou do ponto .)
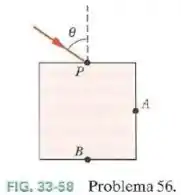
Passo 1
Letra a)
Primeiro precisamos encontrar o ângulo de incidência da luz no ponto . Cada cor tem um ângulo de refração no ponto e logo seus ângulos de incidência são diferentes.
Os ângulos de refração do azul e do vermelho serão:
Os valores serão:
Passo 2
Com o ângulo de refração de cada cor, queremos agora os ângulos de incidência no ponto .
Esse ângulo vai ser .
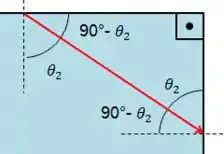
O ângulo de refração da luz que deixa a gota no ponto vai ser dado pela Lei de Snell novamente. Nesse caso:
Como e :
Vamos fazer para cada cor:
A dispersão angular na saída do ponto vai ser:
Passo 3
Letra b)
O ângulo de reflexão no ponto é igual ao ângulo de incidência, .
Porém, ao incidir no ponto , o ângulo de incidência será .
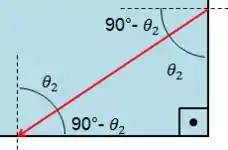
E nesse caso a lei de Snell ficará:
Mas calma lá. Vimos antes que:
Juntando as duas equações:
O que vale para todas as cores. Isso significa que as cores saem paralelas umas às outras no ponto e a dispersão é zero.
Resposta
Letra a)
Letra b)