Fórmulas de Hidrostática

Hidrostática é uma área da física que estuda os fluídos sem que eles estejam em movimento, e possuí diversos conceitos e fórmulas como vamos apresentar a seguir!

Então bora conhecer as fórmulas de hidrostática?

Densidade

A densidade, também conhecida como massa específica é a razão entre a massa de um objeto e o volume que ele ocupa. Escrevemos sua fórmula assim:

Pelo SI a densidade tem unidade de .

Pressão

Por definição a pressão é igual a força sobre a área na qual a força esta sendo aplicada.

Entretanto aqui na hidrostática a gente vai ver uma fórmula um pouquinho diferente, mas o significado é o mesmo:

Onde:

• é a pressão em
• é a densidade do fluido em
• é a aceleração da gravidade em
• é a altura da coluna de fluido em

Empuxo

O empuxo é uma força que envolve o volume de liquido deslocado por um objeto parcialmente ou totalmente submerso em um determinado fluido. Também leva em conta a densidade do fluído em questão e a gravidade no local .

O empuxo pode ser calculado pela seguinte fórmula:

Teorema de Stevin

O teorema de Stevin diz que a variação de pressão dentro de um tubo cheio de fluido, vai ser proporcional ao tamanho da altura da coluna de fluído dentro de tubo, uma altura maior, gera uma variação maior de pressão.

Exemplo: Uma piscina de saltos ornamentais cheia d’agua está sendo observada por uma criança que ama física, ela quer descobrir qual pressão os mergulhadores vão sentir ao dar seus mergulhos. Ela já sabe que caso o mergulhador alcance o ponto B no seu salto, ele vai sentir uma pressão de . Sabendo que a piscina está cheia d`água com uma densidade de e que a atmosfera local vale . Calcule a profundidade do ponto e a pressão no ponto .

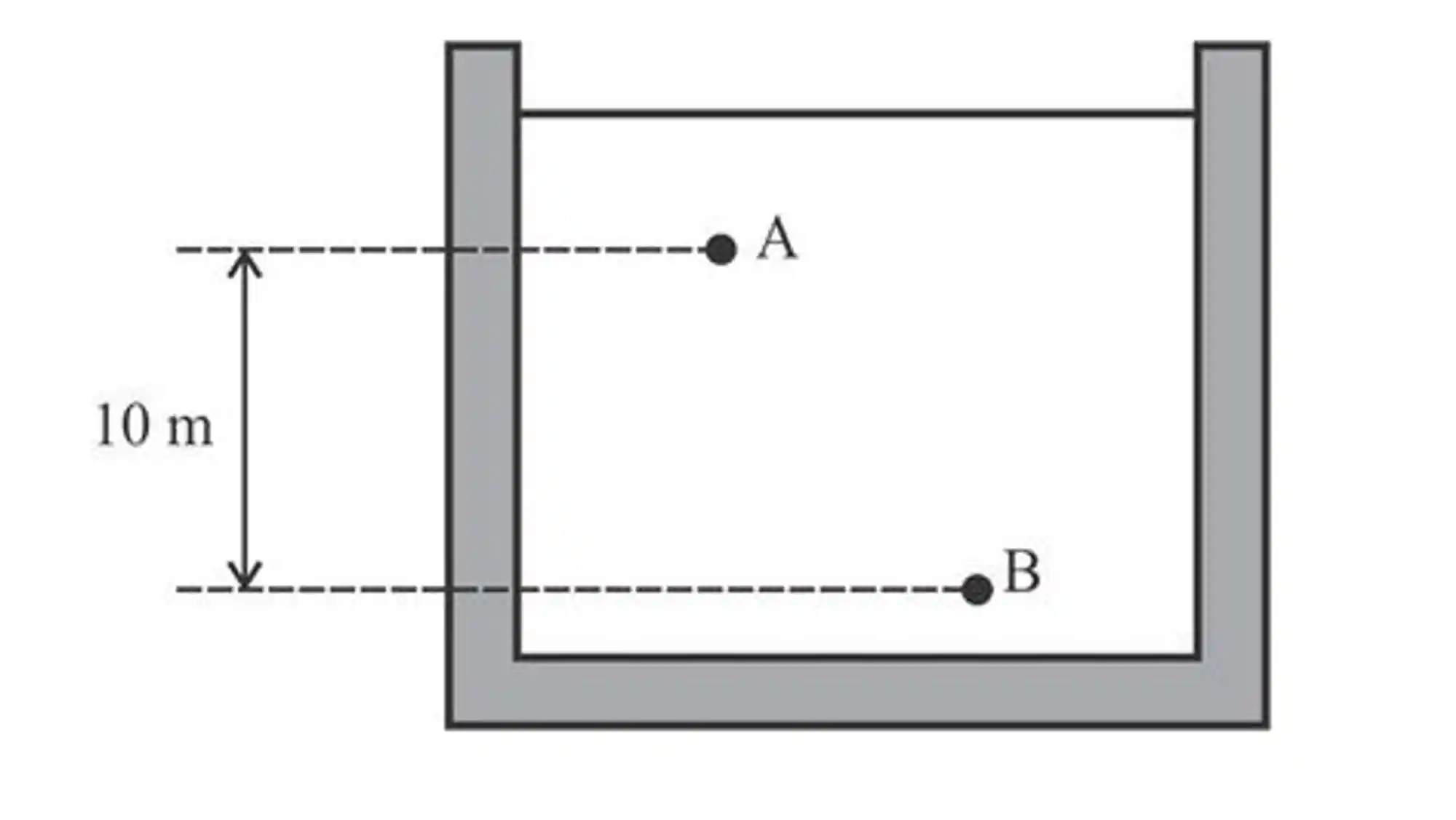
Para descobrir a profundidade do ponto , vamos considerar que a pressão no ponto equivale a pressão atmosférica mais a pressão da coluna d’água a cima do ponto , chamada de pressão hisdrostática. Ou seja, tanto a atmosfera (massa do ar) quanto a massa d’água fazem influência de pressão em cima do ponto contribuindo para o valor da pressão no ponto :

Aplicando o teorema de Stevin:

Isolando :

Substituindo os valores:

O ponto está a uma profundidade de . A pressão no ponto , pelo teorema de Stevin, vai ser equivalente a pressão no ponto , menos a coluna de água que existe entre os pontos e .

Imagine que a gente está pegando a pressão do ponto que nós sabemos, e tirando toda a massa d’água que existe entre e , dessa forma encontrando a pressão no ponto :

Prontinho, agora você pode dar uma conferida no nosso conteúdo sobre Fluidos! Aqui no Responde Aí temos conteúdo em texto, vídeo, exercícios resolvidos passo a passo e mais!

Você também pode clicar aqui pra conferir a resolução de milhares de questões de livro! 🤩🤩🤩