Primeira Lei de Newton
Teoria
O que é uma força?
Exercer uma força em um objeto é a ideia de puxar ou empurrar esse objeto. Por exemplo, quando você está segurando uma caixa pesada, você está fazendo uma força para evitar que ela caia.
Quando estudamos força, é importante ter em mente que existem as leis de Newton que servem como base para análise de qualquer problema.
A primeira lei, nada mais é do que o que você sente sempre ao andar de ônibus.
Lembra quando você está no ônibus, andando a uma velocidade "segura" pelas ruas, e o motorista entra na curva tentando fazer o ônibus tombar (e conseguindo, em alguns casos) fazendo você sentir como se fosse voar pela janela? Isso acontece porque quando o ônibus faz a curva, a sua tendência é continuar seguindo reto, mas o ônibus te "força" a fazer a curva.
Este é o fenômeno conhecido como inércia, muitas vezes usado no cotidiano para fazer uma comparação com pessoas que não saem do lugar se alguma força externa não tirá-la de lá. Você pode usar dessa analogia e lembrar, sempre que vir um corpo que não está sofrendo força alguma, ou a resultante de suas forças é zero, que sua velocidade não vai ser alterada. Se o corpo já estiver em repouso, sua velocidade continua sendo zero. Já já você vai ver o que é e como se calcula a força resultante em um corpo.
Unidade de força – Newton (N)
Em homenagem ao pai da Dinâmica, a unidade que mede a intensidade das forças que agem nos corpos foi intitulada Newton, e tem a letra N como símbolo. Lembrando do assunto de Análise Dimensional, temos que, no SI:
Força como um vetor
Você já aprendeu que os vetores possuem três características que o definem:
- Módulo: é o “tamanho” do vetor, no caso da força, é a intensidade dela;
- Direção: é a reta onde a força está sendo aplicada, exemplo: horizontal, vertical, etc...
- Sentido: é pra onde o vetor está “apontando”, exemplo: pra esquerda, pra cima, etc...
A força é um vetor, e só estará totalmente definida, quando as três características acima estiverem designadas. Vale lembrar que quando expressarmos a força sem o vetor em cima dela, estamos nos referindo ao módulo da mesma.
O que é e como calcular a força resultante – Diagrama de Corpo Livre
Corpos normalmente estão sob ação de várias forças, e, para analisa-las, usamos o Diagrama de Corpo Livre, que nada mais é que um diagrama onde colocamos as forças, com suas direções e sentidos corretos.
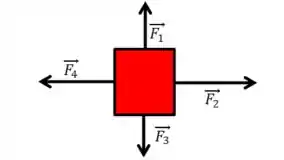
Como visto anteriormente, a soma de vetores tem algumas peculiaridades, e você deve lembrar delas quando for fazer o cálculo da força resultante, que nada mais é que a soma vetorial de todas as forças que agem no corpo. Com isso, podemos concluir que: se a soma vetorial de todas as forças que atuam no corpo for zero, dizemos que o corpo está em equilíbrio, e, segundo a primeira lei, a sua velocidade se manterá constante.
Unidade de força – Newton (N)
Força como um vetor
O que é e como calcular a força resultante – Diagrama de Corpo Livre
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 117-6
Sob a ação de duas forças, uma partícula se move com velocidade constante . Uma das forças é . Qual é a outra?
Passo 1
A parte mais importante do enunciado é a que diz que a partícula se move com velocidade constante. Com isso, sabemos que a resultante das forças que age no corpo é nula.
E sabendo disso, nós conhecemos a primeira lei de Newton, que nos confirma que:
Passo 2
Usando então a primeira lei:
E então encontramos a força que procurávamos:
Resposta
Exercício Resolvido #2
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 115-3
A Fig. 5-22 mostra vistas superiores de quatro situações nas quais forças que atuam sobre um bloco que está em um piso sem atrito. Se os módulos das forças forem escolhidos apropriadamente, em que situações é possível que o bloco esteja (a) em repouso e (b) se movendo com velocidade constante?
Passo 1
A primeira coisa a se perceber nesse exercício é que as letras a e b têm a mesma resposta, já que, nas duas situações, a aceleração do corpo é zero e, portanto, a resultante das forças é nula.
Passo 2
Agora podemos analisar caso a caso.
- possui uma componente vertical, que não é balanceada por , portanto, não há resultante nula.
- Se o módulo das forças forem iguais, a resultante será nula.
- Com o mesmo motivo da situação (1), e possuem componentes verticais para o mesmo sentido, o que não deixa a resultante ser nula.
- A força tem componentes horizontal e vertical e as duas no sentido contrário das forças e , portanto, se essas componentes tiverem módulos apropriados, a resultante pode ser nula.
Resposta
a) 2 e 4
b) 2 e 4
Exercício Resolvido #3
UFF-P1-2014.2-9M
A figura mostra duas forças de mesma magnitude agindo sobre um corpo. Se a magnitude comum das forças é e o ângulo é , que terceira força fará com que o corpo fique em equilíbrio.
- apontando para a direita.
- apontando para a direita.
- apontando para a direita.
- apontando para a esquerda.
- apontanto para a esquerda.
Passo 1
Pensando no equilíbro, precisamos que a soma de todas as forças sobre o sistema seja nula, ou seja
Como temos 3 vetores o nosso problema será
E ainda podemos dividir essa equação em 2 fazendo a decomposição em e
Passo 2
Beleza! Mas quem são essas componentes? Pro vetor temos uma componente negativa (que aponta para esquerda) e uma componente positiva (que aponta para cima), assim
Pelo enunciado o módulo do vetor é , assim
Já pro vetor 2 temos algo parecido, só que a sua componente aponta para baixo
O enunciado nos conta que o módulo de também é , assim
Passo 3
Agora podemos voltar pras equações do passo 1!
Primeiramente na direção
Agora na direção
O nosso vetor então será
Isso aí é um vetor que aponta na direção positiva de , ou seja, é um vetor de módulo que aponta para direita!
Resposta
Letra a)
Exercício Resolvido #4
UFF-P1-2014.2-10M
Um objeto move-se com velocidade constante relativamente a um sistema de referência inercial. Qual das afirmações abaixo é necessariamente verdadeira?
- Não há forças agindo sobre o objeto.
- Uma pequena força age sobre o objeto, na direção do movimento.
- A força resultante sobre o objeto é zero.
- Duas afirmações anteriores são necessariamente verdadeiras.
- Todas as afirmações anteriores são falsas.
Passo 1
Cuidado pra não se confundir nessa questão!
Se não existem forças agindo sobre um corpo, ele tem que estar em repouso ou se movimentando com velocidade constante.
Mas quando dizemos que um corpo está se movimentando com velocidade constante não significa que não há forças agindo sobre ele. Podem sim haver forças agindo sobre ele.
A única coisa que podemos afirmar é que a resultante das forças agindo sobre o corpo é nula!
Resposta
Letra c)
Exercício Resolvido #5
Brasil Escola
De acordo com a Dinâmica, dizemos que um corpo está em equilíbrio quando:
a) sua velocidade é nula
b) seu movimento é retilíneo
c) sua aceleração é constante
d) sua aceleração é nula
e) o módulo da força resultante sobre o corpo é maior que zero
Passo 1
Como nós vimos na teoria, mesmo em movimento, um corpo pode estar em equilíbrio; nesse caso, dizemos que o seu equilíbrio é dinâmico, pois a sua aceleração é igual a zero. Dessa forma, quando a aceleração de um corpo é nula, ele se encontra em equilíbrio! Show!
Resposta
d) sua aceleração é nula
Exercício Resolvido #6
Uma haste, submetida às forças indicadas na figura, está presa a um eixo fixo em uma das suas extremidades. Sabendo-se que a haste pode girar livremente e que , podemos dizer que a resultante das forças que agem sobre a haste será zero se a força aplicada pelo eixo na haste for tal que:
(a) suas componentes e são ambas positivas.
(b) sua componentes e são ambas negativas.
(c) sua componente é nula e sua componente é igual à componente de .
(d) sua componente é positiva e sua componente é nula.
(e) sua componente é negativa e sua componente é antiparalela à componente de .
Passo 1
Precisamos descobrir o sentido das componentes e da força que será aplicada ao eixo para que a barra esteja em equilíbrio, pra isso vamos começar desenhando na barra essas componentes e também a decomposição da força .
As componentes foram representadas com aquele sentido ali apenas para fazermos os cálculos, se por acaso encontrarmos sinais diferentes vamos trocar a direção das forças.
Com esse esquema da barra faremos o equilíbrio das forças nos eixos e , com as equações:
Passo 2
Vamos dar uma olhada pro eixo , pelo equilíbrio teríamos o seguinte:
Com isso a gente vê que o sentido do desenho foi adotado certo! Como só temos uma força em que é para a esquerda, a componente horizontal deve ser para a direita para equilibrar a barra.
Passo 3
Para o eixo faremos bem parecido, só fazer o equilíbrio das forças:
Po, mas e aí, tenho muitas incógnitas e não dá pra saber a direção de .
Lembra da condição que o enunciado nos deu? Vamos usar ela ali na nossa equação.
Ué, mas quem diabos é
Calma, é o nome carinhoso que o enunciado deu pro módulo da componente de . Vamos rearrumar essa equação toda pra um lado só da igualdade e jogar lá na equação do equilíbrio, ok?
Logo:
Poxa, mas lá em cima os valores não estão em módulo, podemos substituir mesmo assim? Lembra que o módulo retorna o valor absoluto?
Lá em cima temos a mesma configuração, é a mesma diferença em termos de valor absoluto sacou? Desse jeito podemos dizer que:
Então a equação anterior fica:
Então a componente também será positiva.
Resposta
(a)
Exercício Resolvido #7
ITA
Um corpo é impulsionado, no vácuo, sobre um plano horizontal, sem atrito, por uma força paralela ao plano, que atua instantaneamente sobre ele. Neste caso, pode-se concluir que:
a) o corpo adquire movimento uniformemente acelerado, no qual permanece indefinidamente.
b) o corpo segue em equilíbrio.
c) durante o movimento, não atua força sobre o corpo.
d) o corpo possui movimento retardado.
e) o corpo adquire movimento retilíneo uniforme a partir do repouso.
Passo 1
Pela Primeira Lei de Newton sabemos que um corpo estará em equilíbrio quando a força resultante agindo sobre o mesmo for igual a zero (Fr = 0).
A força é aplicada instantaneamente e deixa de atuar, então quando o corpo está em movimento, desenvolvendo uma certa velocidade, não haverá mais sobre ele nenhuma força atuando, já que não existe atrito nem resistência do ar.
Assim podemos afirmar que se Fr = 0, o corpo se move em velocidade constante. Logo, o corpo está em equilíbrio, obedecendo a Lei da Inércia.
Resposta
b) o corpo segue em equilíbrio.
Exercício Resolvido #8
UFRN
Considere um grande navio, tipo transatlântico, movendo-se em linha reta e com velocidade constante (velocidade de cruzeiro). Em seu interior, existe um salão de jogos climatizado e nele uma mesa de pingue-pongue orientada paralelamente ao comprimento do navio.
Dois jovens resolvem jogar pingue-pongue, mas discordam sobre quem deve ficar de frente ou de costas para o sentido do deslocamento do navio. Segundo um deles, tal escolha influenciaria no resultado do jogo, pois o movimento do navio afetaria o movimento relativo da bolinha de pingue-pongue.
Nesse contexto, de acordo com as leis da física, pode-se afirmar que:
a) a discussão não é pertinente, pois, no caso, o navio se comporta como um referencial não inercial, não afetando o movimento da bola
b) a discussão é pertinente, pois, no caso, o navio se comporta como um referencial não inercial, não afetando o movimento da bola
c) a discussão é pertinente, pois, no caso, o navio se comporta como um referencial inercial, afetando o movimento da bola
d) a discussão não é pertinente, pois, no caso, o navio se comporta como um referencial inercial, não afetando o movimento da bola
Passo 1
Como o transatlantico se move em linha reta com velocidade constante, ele está em equilibrio dinâmico e comporta-se como se estivesse em repouso (equilibrio estático), não afetando o movimento da bola, sendo assim ele se comporta como um referencial inercial.
Resposta
d) a discussão não é pertinente, pois, no caso, o navio se comporta como um referencial inercial, não afetando o movimento da bola