Segunda Lei de Newton
Produzido por Ludovic BeghinTeoria
Tá bom, já entendi a Primeira Lei e lá vem esse cara com outras duas...
Mas meu jovem, não fica chateado com o tio Newton não, porque ele mandou bem nessa lei, sabe o porque?
Porque agora a gente consegue relacionar uma força com um movimento!

Calma... olha só aqui essa situação.
Imagina que temos um bloco de massa 5:

Se não fizermos nada, ele vai continuar lá parado.
Mas e se uma força começar a puxar esse bloco para direita?
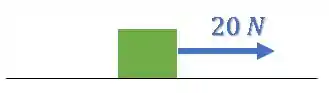
Bom, esse bloco vai começar a andar para a direita, certo?
Isso porque a força gera nele uma aceleração , e por isso ele começa a ganhar velocidade.
Show!
Mas qual será essa aceleração do bloco?
Força e aceleração
Pela Segunda Lei de Newton, podemos dizer que:
Ou seja, a força é igual a massa do bloco vezes a aceleração .
Repara ainda que para essa mesma força, se o bloco tiver uma massa maior, sua aceleração é será menor:
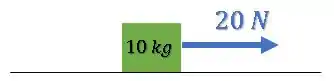
Como o bloco é mais pesado, faz sentido que ele ganhe velocidade mais devagar, né?
Força Resultante
Bom, mas e se eu tiver mais de uma força atuando sobre o bloco??
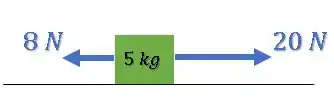
Ainda na Segunda Lei de Newton, temos que calcular a Força Resultante , que é a soma de todas as forças:
A gente escolhe um dos sentido como positivo (por exemplo para a direita):
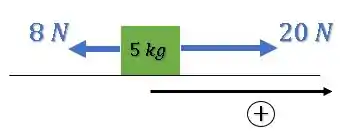
E temos que:
Ou seja, essa situação com duas forças é o mesmo que apenas uma força para a direita igual à força resultante:
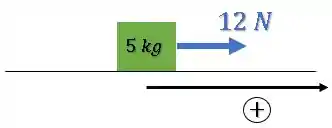
Parabéns, você já entendeu a Segunda Lei de Newton.

Bommm, na verdade tem mais um detalhezinho, olha só a definição mais formal...
A Segunda Lei de Newton completa

O detalhezinho a mais é que na verdade estamos tratando de vetores. Então:
Ou seja, podemos calcular o vetor força resultante (soma de todas as forças sobre o corpo) e assim a aceleração desse corpo estará na mesma direção e sentido.
Vamos ver um exemplo disso.
Analisando a segunda lei em dois eixos
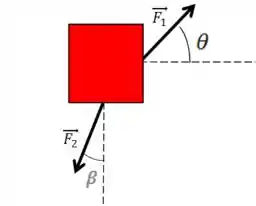
Para descobrir a aceleração desse bloco de massa , devemos aplicar a Segunda Lei de Newton:
Mas quem é o vetor força resultante ?
Ele será a soma de todas as forças sobre o bloco, ou seja:
Normalmente, para evitar o uso da soma vetorial, usamos da decomposição das forças nos eixos e , e depois usamos a equação da segunda lei duas vezes, uma para cada eixo.
Decomposição de um vetor
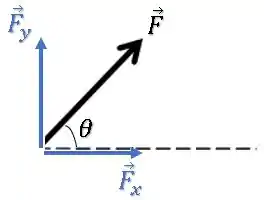
Para achar as componentes e , nós fechamos um triângulo retângulo:
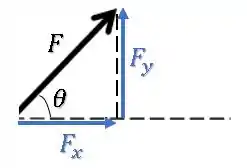
Para a componente horizontal, temos:
Já para a componente vertical, temos:
Ou seja, para a componente COlada no ângulo, nós usamos COS, enquanto para a componente SEparada do ângulo, nós usamos SEN.
Hahaha meio bobo, mas são as bobeiras que a gente grava.
Voltando ao nosso exemplo...
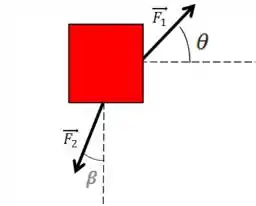
Decompondo a primeira força, temos:
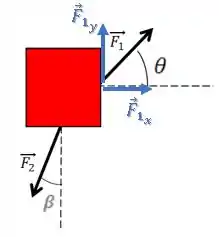
Decompondo a segunda força, temos:
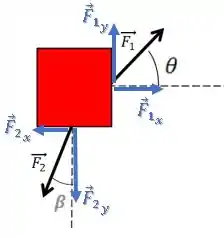
Repara que agora a componente “colada” no ângulo é a componente vertical, enquanto a componente “separada” é a componente horizontal, então:
Agora vamos aplicar a Segunda Lei para cada um dos eixos e descobrir a aceleração.
No eixo , temos:
Escolhendo o sentido positivo para a direita:
Já no eixo y, temos:
Escolhendo o sentido positivo para cima:
Então, o vetor aceleração do nosso bloquinho será:
OBS: Caso precisemos achar o módulo desse vetor, podemos recorrer novamente ao triângulo retângulo.
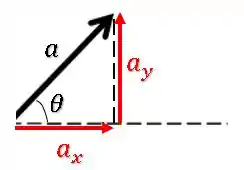
Aplicando Pitágoras, temos:
Equilíbrio de Forças
Para fechar, se um corpo estiver em equilíbrio de forças isso significa que a Força Resultante sobre ele é nula:
Assim, pela Segunda Lei de Newton, temos que:
Chegamos na Primeira Lei de Newton (inércia), haha.
Ou seja, é um caminho de mão dupla...
Sempre que a Força Resultante for zero, não há aceleração.
Sempre que a aceleração for zero, não há Força Resultante.
É isso, agora vamos treinar nos exercícios :)
Força Resultante
A Segunda Lei de Newton completa
Analisando a segunda lei em dois eixos
Decomposição de um vetor
Equilíbrio de Forças
Exercícios Resolvidos
Exercício Resolvido #1
UNICAMP-P1-2014.2A-Q9
Um corpo de massa parte do repouso e após sua velocidade é de . Considerando que o corpo foi submetido a uma força externa constante, responda:
Qual é o módulo da força externa?
a)
b)
c)
d)
e)
Passo 1
Temos uma força externa sendo aplicada num corpo.
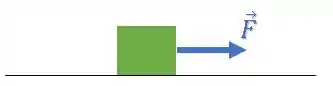
Utilizando a segunda lei de Newton temos que:
Já sabemos a massa do corpo, porém quem é a aceleração?
Passo 2
Se a força é constante, temos que a aceleração também será constante.
Assim, o nosso corpo está realizando um Movimento Uniformemente Acelerado, o que é bem comum nos exercícios de Segunda Lei de Newton.
Então, nós podemos utilizar a equação de velocidade para um MUV:
Como o corpo parte do repouso, sua velocidade inicial é zero:
Assim, após , temos:
Passo 3
Agora que achamos a aceleração, basta substituir na Segunda Lei de Newton:
Resposta
Letra (d)
Exercício Resolvido #2
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 116-5
A Fig. 5-24 mostra o diagrama de corpo livre de quatro situações nas quais um objeto, visto de cima, é puxado por várias forças em um piso sem atrito. Em quais dessas situações a aceleração do objeto possui:
(a) uma componente ?
(b) uma componente ?
(c) Em cada situação, indique o sentido de indicando um quadrante ou um sentido ao longo de um eixo. (Isso pode ser feito com alguns cálculos mentais.)
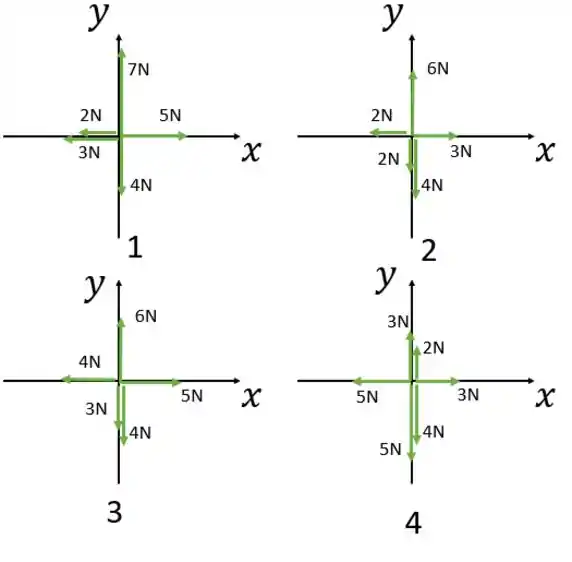
Passo 1
Vamos partir da Segunda Lei de Newton:
Ou seja, a aceleração do corpo está na direção e sentido da força resultante .
Faremos a soma vetorial das forças para chegarmos na força resultante, e encontraremos a aceleração usando a segunda lei de Newton.
Passo 2
Analisando caso a caso, temos:
Diagrama 1:
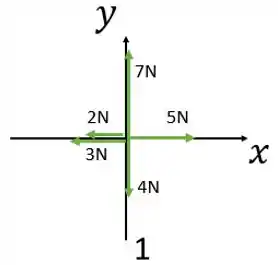
A componente da força resultante na direção do eixo é:
A componente da força resultante na direção do eixo é:
Então, temos que o vetor força resultante será:
Diagrama 2:
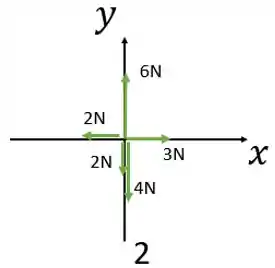
A componente da força resultante na direção do eixo é:
A componente da força resultante na direção do eixo é:
Então, temos que o vetor força resultante será:
Diagrama 3:
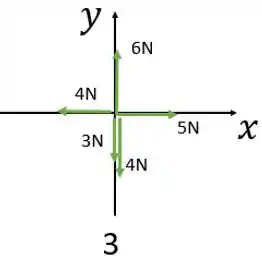
A componente da força resultante na direção do eixo é:
A componente da força resultante na direção do eixo é:
Então, temos que o vetor força resultante será:
Diagrama 4:
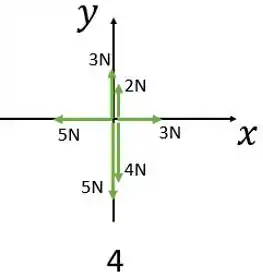
A componente da força resultante na direção do eixo é:
A componente da força resultante na direção do eixo é:
Então, temos que o vetor força resultante será:
Passo 3
Agora que descobrimos os vetores de Força resultante, sabemos a direção do vetor aceleração , pois é o mesmo do vetor Força resultante .
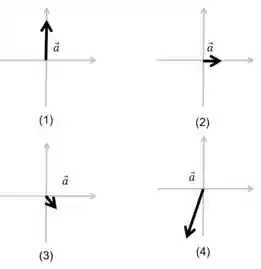
Diagrama 1:
A força resultante apresenta apenas uma componente positiva na direção do eixo , logo:
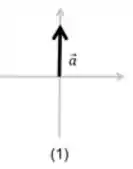
Diagrama 2:
A força resultante apresenta apenas uma componente positiva na direção do eixo , logo:
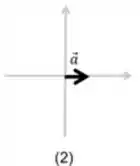
Diagrama 3:
A força resultante apresenta uma componente positiva na direção do eixo e uma componente negativa na direção do eixo , logo:
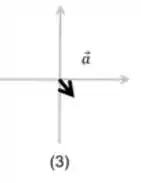
Diagrama 4:
A força resultante apresenta uma componente negativa na direção do eixo e uma componente negativa na direção do eixo , logo:
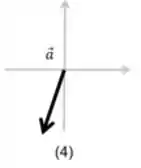
Resposta
- 2, 3 e 4
- 1, 3 e 4
Exercício Resolvido #3
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 117-5
Duas forças agem sobre a caixa de vista de cima na Fig.5-31, mas apenas uma é mostrada. Para , e , determine a segunda força (a) em termos dos vetores unitários e como um (b) módulo e (c) um ângulo em relação ao semieixo positivo.
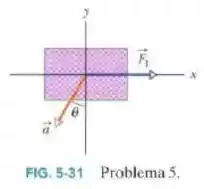
Passo 1
Primeiro de tudo, esquece aquela força ...
Vamos à Segunda Lei de Newton:
Então, se conhecemos a aceleração e a massa , podemos encontrar a força resultante sobre a caixa.
Sendo o vetor na mesma direção e sentido que o vetor .
Passo 2
Qual a ideia agora?
Bom, existem duas forças agindo sobre a caixa.
A força nós conhecemos, mas a nós não conhecemos:
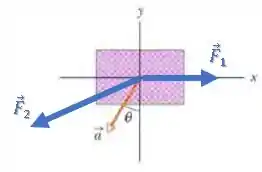
Mas sabemos que a força resultante (conhecida) será a soma delas:
Passo 3
Vamos escrever o vetor Força Resultante em termo de suas componentes.
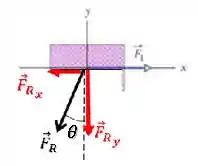
A componente vertical está “colada” no ângulo, então ela será a componente com o cosseno, enquanto a componente na horizontal está “separada” do ângulo, então terá o seno:
Fazendo essas continhas, temos:
Podemos escrever o vetor .
Tanto a componente na horizontal quanto a componente na vertical estão no sentido negativo do eixo, logo:
Passo 4
Agora que já temos a força resultante fica mole!
Voltando à relação de que a é a soma de todas as forças sobre o corpo, temos:
Aqui, temos a opção de trabalhar com cada eixo separadamente, ou então, usar a equação na própria forma vetorial.
Vamos usar direto na forma vetorial!
Como a força (conhecida) está na direção positiva do eixo , o vetor será:
Substituindo os vetores na expressão, temos:
Assim, respondemos a letra (a).
Passo 5
Na letra (b), queremos o módulo da força .
Para achar o módulo de um vetor, basta fecharmos um triângulo retângulo com as suas componentes e aplicarmos Pitágora:
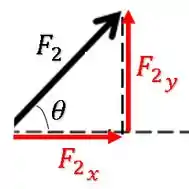
Não se preocupe com desenhar o retângulo na orientação certiiiinha, pois o Pitágoras vai funcionar da mesma maneira.
O importante é que as componentes são perpendiculares.
Assim, temos:
Respondida a letra (b).
Passo 6
Agora na letra (c), queremos um dos ângulos entre a força e o semi-eixo positivo .
Então, primeiro vamos descobrir o ângulo de inclinação de com relação a horizontal.
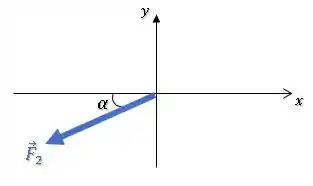
Para achar o ângulo , podemos partir das componentes horizontal e vertical.
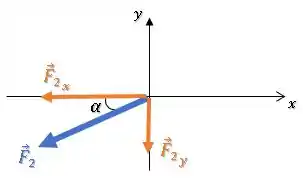
Fechar um triângulo com as componentes horizontal e vertical e usar alguma das identidades trigonométricas:
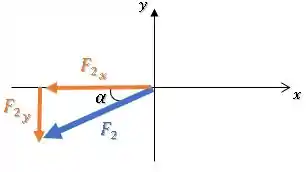
Como não é nenhum dos ângulos notáveis (30°, 45° ou 60°), precisamos usar a calculadora e calcular o arcotangente de , para descobrir o arco cuja tangente vale :
Para obter um dos dois ângulo entre e o semi-eixo positivo , basta somar :
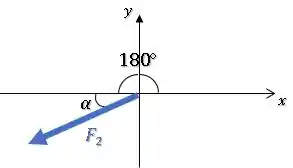
Respondemos a letra (c).
OBS: O segundo ângulo entre e positivo seria.
Resposta
Exercício Resolvido #4
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 119-29
Um elétron com penetra horizontalmente em uma região onde está sujeito a uma força vertical constante de . A massa do elétron é . Determine a deflexão vertical sofrida pelo elétron enquanto percorre uma distância horizontal de
Passo 1
Vamos fazer um desenho para facilitar a compreensão:
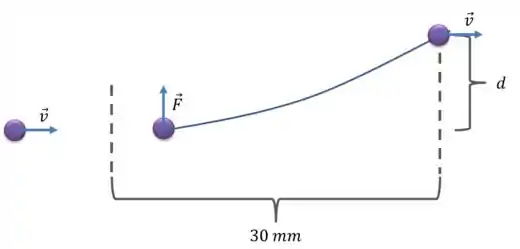
Bom, como a força atua na vertical sobre a partícula, a aceleração também será apenas na vertical.
Ou seja, temos um Movimento Uniformemente Variado em .
Além disso, como a velocidade na horizontal não varia (não há aceleração horizontal), a particula realiza um Movimento Uniforme em .
Passo 2
Agora que sabemos a direção e o sentido da aceleração do elétron, precisamos descobrir seu módulo. Temos a força aplicada a ele e a massa do mesmo. O que podemos usar? Isso mesmo! A segunda lei de Newton!
Substituindo os valores de e :
Passo 3
Como já vimos que a velocidade horizontal se mantém a mesma, para descobrirmos o tempo que o elétron demora para percorrer os , basta lembrar que este é um MRU:
Então, podemos utilizar a equação:
Passo 4
Conhecendo o quanto esse movimento durou, podemos analisar o movimento na vertical .
Como a partícula só apresenta velocidade na horizontal inicialmente, temos:
Então, temos:
Substituindo os valores encontrados:
Resposta
Exercício Resolvido #5
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 118-12
Duas forças horizontais e agem sobre um disco de que desliza sem atrito sobre o gelo, no qual foi desenhado um sistema de coordenadas . A força aponta no sentido positivo do eixo e tem módulo de . A força tem um módulo de . A Fig. 5-34 mostra a componente da velocidade do disco em função do tempo . Qual é o ângulo entre as orientações constantes das forças e ?
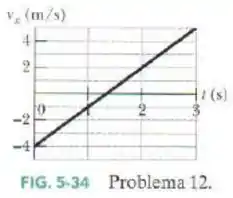
Passo 1
Fala pessoal, vem comigo pra mais um?
Vamos fazer um desenho para entendermos o que tá se passando.
A Força está na direção do eixo .
Já a força está numa posição qualquer, então vamos colocar com um ângulo qualquer da :
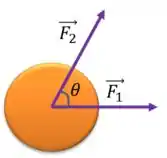
A ideia é que com o gráfico da velocidade sobre o tempo, conseguimos a aceleração no eixo . Feito isso, podemos aplicar a Segunda Lei de Newton e descobrir a força resultante na direção :
Por fim, podemos relacionar a força resultante com a soma na horizontal de e . E aqui é o seguinte a força horizontal nós temos e também, só vai faltar aí é decompor essa força inclinada pra horizontal, e é aí que o ângulo vai aparecer então fiquem ligados pois é esse ângulo que a gente quer!
Passo 2
Vamos usar o gráfico dado para obter informações.
Observando bem ele, conseguimos ver que o movimento no eixo se trata de um MUV, porque a velocidade varia uniformemente (reta).
A aceleração é a variação da velocidade:
Logo, basta pegar quaisquer dois pontos do gráfico e calcular esse .
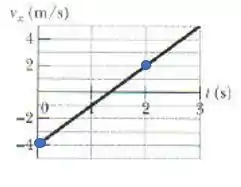
Aqui vou escolher o ponto inicial:
e
E o ponto final:
e
Você poderia ter escolhido outro ponto também se quisesse o ideal é escolher um ponto fácil de trabalhar, assim:
Com a aceleração bora pra força em .
Passo 3
Agora nós temos: a aceleração no eixo e a massa do disco, portanto, podemos usar da segunda lei de Newton para achar a força resultante no eixo :
Com e a aceleração encontrada temos:
Passo 4
Agora, para achar o ângulo vamos fazer o somatório de forças na horizontal.
Bom, mas já está na horizontal, porém não...
Logo, temos que pegar sua componente horizontal:
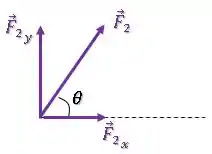
Aqui por trigonometria vamos decompor essa força fazendo a seguinte relação:
E encontramos alguma relação com o ângulo que queremos, vamos dar um jeito de isolar ele jajá.
Passo 5
Aplicando a segunda lei de Newton temos que o somatório das forças horizontais é:
Beleza, conhecemos todo mundo aqui mas antes vamos isolar o cosseno do ângulo pra encontrar o ângulo depois!
Vamos substituir os valores calculados e dados do enunciado.
Substituindo na equação temos:
Agora pra encontrar o ângulo vamos fazer a trigonométrica inversa, mas o que é isso? Pro cosseno a inversa é conhecida como arcocosseno, e a gente lê como se fosse “O arco cujo cosseno é ”. E aí você inverte, tira o do cosseno e coloca no número que você calculou.
Talvez na sua calculadora essa função apareça como , mas não esquenta é a mesma função só vai ficar assim:
Encontramos o nosso ângulo, vamos praticar mais juntos??
Resposta
Exercício Resolvido #6
Halliday 9° edição vol.1 cap.5 seção 6 questão 11
Uma partícula de se move ao longo de um eixo sob a ação de uma força variável. A posição da partícula é dada por , com em metros e em segundos. O fator é constante. No instante , a força que age sobre a partícula tem um módulo de e aponta no sentido negativo do eixo x. Qual é o valor de ?
Passo 1
Fala aí! Sabemos que a velocidade é a derivada da posição em relação ao tempo e a aceleração é a derivada da velocidade. Assim:
De acordo com a Segunda Lei de Newton, temos que :
Sabemos que no instante , . Dessa forma :
Logo,
.
Tranquilo, né? Show demais!
Resposta
Exercício Resolvido #7
Halliday 9° edição vol.1 cap.5 seção 6 questão 10
Uma partícula de se move ao longo de um eixo de acordo com a equação , com em metros e em segundos. Qual é, na notação dos vetores unitários, a força que age sobre a partícula no instante ?
Passo 1
Pra gente resolver essa questão aqui a gente tem que lembrar que a aceleração é a derivada segunda da função posição e que a força está relacionada à aceleração através da Segunda Lei de Newton. Derivando duas vezes a função do espaço, que é em relação a t, temos:
Passo 2
A força que age sobre a partícula no instante , é dada por :
Show de bolinhas! :D
Resposta
Exercício Resolvido #8
UFPE 2018.1
Sobre um corpo, de massa , atuam três forças, , e . Duas delas, mostradas na figura abaixo à esquerda, tem módulos iguais a , mas atuam em direções diferentes. O corpo está inicialmente em repouso sobre uma mesa horizontal sem atrito. Na figura da direita, é mostrado um gráfico da velocidade escalar do corpo em função do tempo, onde cada quadrado na vertical equivale a . Considere e .
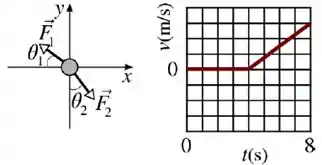
No intervalo entre e sabe-se que o copo se desloca em uma trajetória retilínea no sentido positivo do eixo . Neste intervalo de tempo a força é dada por:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Passo 1
Entre os instantes e , a gente consegue ver no gráfico que a partícula começa a se mover com uma certa aceleração.
Inclusive conseguimos calcular essa aceleração, pois:
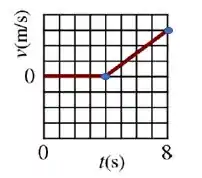
Como cada quadradinho na vertical é igual a , temos que:
Além disso, conseguimos aplicar a Segunda Lei de Newton para encontrar a força resultante agindo sobre a partícula, pois sabemos que a massa é :
O enunciado não disse que a partícula se movimenta na direção positiva do eixo ?
Isso significa que a força resultante sobre o corpo deve estar nessa direção, então:
Passo 2
Essa força resultante será a soma vetorial das três forças atuando sobre o corpo:
Conhecemos tanto a , quanto a , assim conseguimos encontrar a .
Então, vamos decompor essas duas forças que conhecemos para somar as componentes nos eixos e .
Passo 3
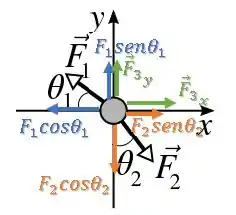
Decompondo primeiro , temos:
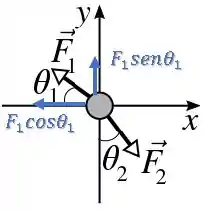
Decompondo agora , temos:
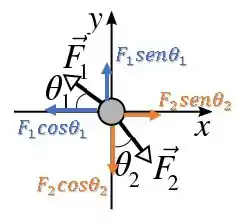
Além disso, existe também a que até agora é desconhecida, então vamos considerar uma componente em e uma em nos sentidos positivos. Mas, depois de realizar as contas vamos saber realmente o sentido dessas componentes:
Passo 4
Agora, vamos somar todas essas componentes para achar a força resultante e igualar com o valor que encontramos no Passo 1.
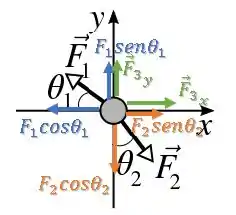
Na direção do eixo , temos que a força resultante é igual a :
Substituindo os valores que temos no enunciado de , e os senos e cossenos:
Enquanto no eixo , a força resultante é nula:
Juntando as duas componentes de , ficamos com o vetor:
Ficamos com a letra (g).
Resposta
Letra g.