11.20P Três esferas, cada uma com massa , estão dispostas nos vértices de um triângulo equilátero de lado . A) Mostre que a força gravitacional sobre cada esfera dirige-se para o centro do triângulo e calcule a intensidade de tal força. B) Mostre que em um movimento sincronizado das esferas, elas podem orbitar em torno do centro de massa comum, que é o centro do triângulo, e calcule a velocidade angular do sistema.
Passo 1
Belezoca galerinha, se a gente montar esse triângulo, vamos ter que:
Agora se por exemplo a gente fosse montar os pares de força que atuam sobre a esfera da esquerda, teríamos uma atração gravitacional com a esfera superior, e uma atração gravitacional com a esfera ao lado:
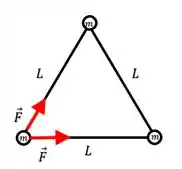
E como temos forças iguais atuando em direções diferentes, a resultante entre elas vai passar pela bissetriz dos vetores, tal que:
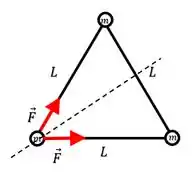
E se a gente traçar retas bissetrizes para todas as massas, vamos obter:
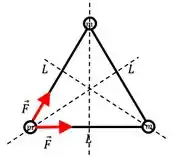
E a interseção entre essas bissetrizes é exatamente o centro do triângulo, logo:
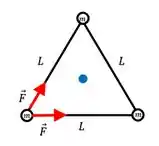
Então sim, a resultante, está apontando para o centro do triângulo.

Passo 2
Iradoso, e agora pra gente calcular a intensidade dessa força, podemos ser malandrinhos mais uma vez e fingir que existe um eixo exatamente onde está a massa que estamos trabalhando:
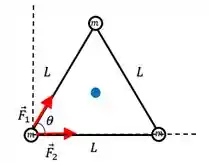
Sendo assim, podemos decompor aquela força que não está no eixo, lembrando que como se trata de um triângulo equilátero, o ângulo entre os lados é de , tal que:
E como essa força, é a força gravitacional entre as partículas de massa distantes pelo lado do triângulo de tamanho , teremos que:
Tal que a força é:
Logo a soma das forças é:
Portanto a força resultante será:
Passo 3
Show de bolinhas, então a intensidade dessa força, vai ser o módulo dela, e se a gente calcular ela, vamos obter que:
Portanto, a intensidade da força é:

Passo 4
Agora, como o sistema está em movimento circular, em torno do centro do triângulo, temos que a força gravitacional resultante, que aponta para o centro, é exatamente igual a força centrípeta devido a rotação:
E essa força centrípeta é dada pelo produto da massa pela aceleração centrípeta:
Onde essa aceleração centrípeta é dada pela expressão:
Em que é a velocidade linear que podemos relacionar com a velocidade angular através da expressão:
Enquanto é distância da massa até o centro do triângulo:
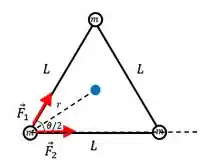
Tal que:
Logo:
Portanto a aceleração centrípeta é:
E a força centrípeta:
Passo 5
Então se a gente igualar as força, vamos obter que:
E isolando a velocidade angular:
Logo:
