Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 22
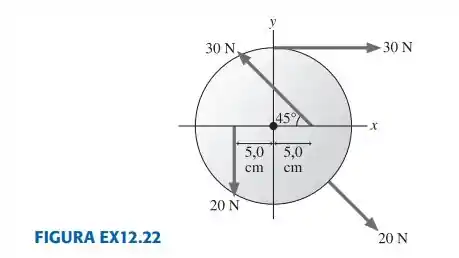
12.22. O disco de 20 cm de diâmetro da figura ex12.22 pode girar em torno de um eixo que passa pelo centro. Qual é o torque resultante em torno do eixo?
Passo 1
O torque resultante é a soma de todos os torques. O que a gente pode fazer aqui é calcular o torque de cada força separadamente e depois somar tudo.
Vamos começar
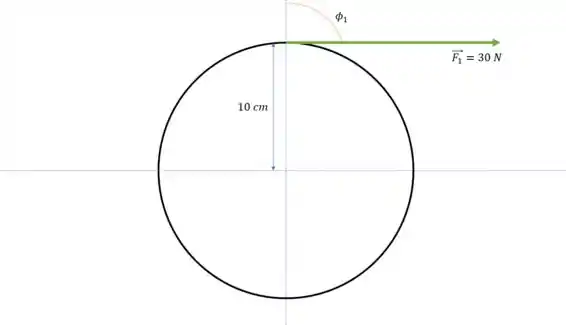
Primeiro o torque gerado por . A gente pode ver pela imagem que o ângulo é , porque está no sentido horário, e a distância é , ou seja, .
Substituindo os valores
Passo 2
Agora vamos para
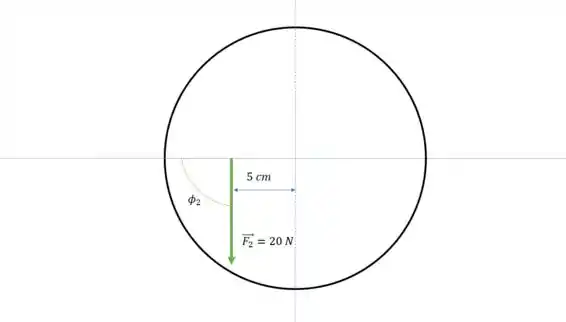
Agora o ângulo é e a distância é , . Então
Passo 3
Agora é a vez de
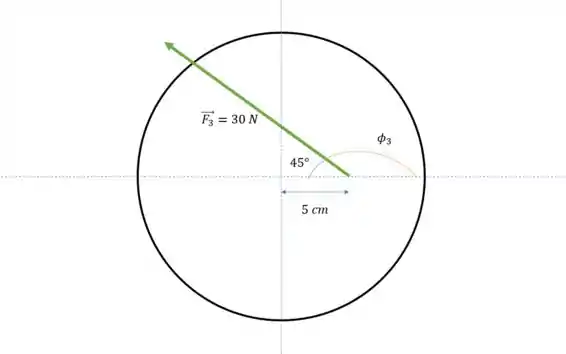
é um pouco mais complicado de descobrir, mas repare que , então . E a distância é de novo. Então
Passo 4
E por último
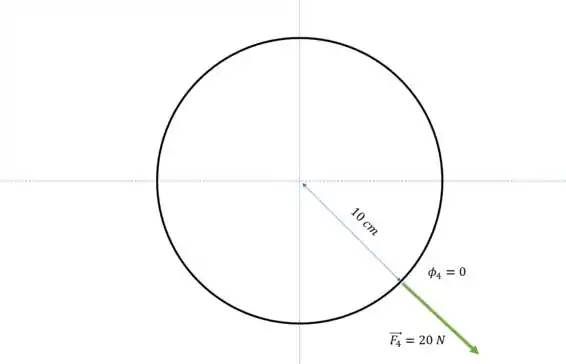
Bom, a força está paralela com a distância, e o ângulo é . Então podemos afirmar que o torque da última força é nulo.
Passo 5
Agora que temos os valores de todos os torques, podemos obter o torque total
Substituindo os valores