Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 21

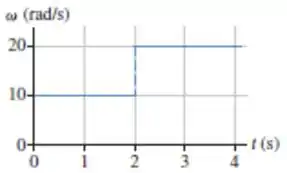
21. A FIGURA EX4.21 mostra o gráfico velocidade angular versus tempo para uma partícula que se move em um círculo. Quantas revoluções ela realiza durante os primeiros 4   s ?

Passo 1

Então temos que saber quantas revoluções a partícula da em 4   s . De uma forma mais clara temos que saber quantas vezes a partícula tem um deslocamento de 2 π .

Para isso vamos usar o gráfico indicado pelo enunciado que nos dá a velocidade angular em função do tempo. Lembrando u o deslocamento angular é dado por:

Δ θ = ω Δ t

Então podemos encontrar o deslocamento total da partícula em 4   s e depois é só dividir por 2 π e assim podemos achar quantas revoluções que a partícula deu.

Passo 2

Vamos lá então encontrar o deslocamento da partícula, mas temos que prestar atenção que a partícula tem velocidades diferentes, temos que de t = 0 até t = 2   s a velocidade angular é 10   r a d / s e de t = 2   s até t = 4   s a velocidade angular é ω = 20   r a d / s .

Vamos então primeiro encontrar o deslocamento de t = 0 até t = 2   s , temos:

Δ θ 1 = 10 ( 2 - 0 )

⇒ Δ θ 1 = 20   r a d

Agora o deslocamento de t = 2   s até t = 4   s . Temos:

Δ θ 2 = 2 0 ( 4 - 2 )

⇒ Δ θ 2 = 4 0   r a d

Então o deslocamento total é:

Δ θ = Δ θ 1 + Δ θ 2

= 20 + 40

Δ θ = 60   r a d

Passo 3

Agora vamos encontrar o número de revoluções da partícula, vamos dividir o deslocamento total por 2 π , assim:

60   r a d 2 π   r a d

= 9,5   r e v o l u ç õ e s

Resposta

9,5   r e v o l u ç õ e s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bola de baseball é lançada de forma que sua velocidade inicial ao perder contato com o taco faz um ângulo de 30 ° acima da horizontal. Ela deixa o taco a uma altura de 1,0m acima do solo e aterris
Um homem balança uma pedra presa a uma corda em um círculo horizontal com rapidez constante. A figura representa o caminho da pedra vista de cima para baixo. (a) Qual dos vetores poderia representar a
Verdadeiro ou falso:(a) Um objeto não pode se mover em círculos a menos que tenha aceleração centrípeta.(b) Um objeto não pode se mover em círculos a mesmos que tenha aceleração tangencial.(c) Um obje
Usando um diagrama de movimento, encontre a direção da aceleração da massa presa na ponta de um pêndulo quando ela está em um ponto onde o sentido do seu movimento é invertido.
No problema 38 , escreva o vetor que descreve o deslocamento de uma mosca se ela vai rapidamente da ponta do vetor dos minutos para a ponta do vetor de horas às 3 : 00P . M .