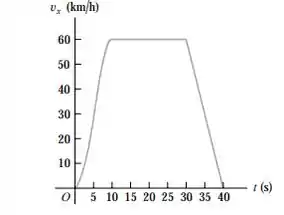
2.14 A Figura 2.34 mostra a velocidade em função do tempo de um carro movido a energia solar. O motorista acelera a partir de um sinal de parada e se desloca durante 20 s com velocidade constante de 60 km/h, e a seguir pisa no freio e para 40 s após sua partida do sinal. a) Calcule sua aceleração média para os seguintes intervalos de tempo: i) t 0 até t 10 s; ii) t 30 s até t 40 s; iii) t 10 s até t 30 s; iv) t 0 até t 40 s; b) Qual é a aceleração instantânea a t 20 s e a t 35 s?

Opa, bora lá! Temos o seguinte gráfico que relaciona a velocidade de uma carro com o tempo:

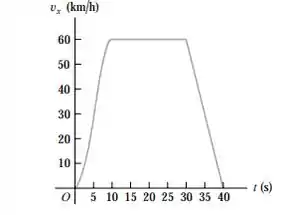
Primeiro queremos saber a velocidade média de 0 a 10 segundos. Teremos que transformar a velocidade para metros por segundo, dividindo por 3,6. Em 10 segundos a velocidade é de 60 km/h, dividindo por 3,6, temos:

Vamos lembrar que , pimpolhos!. Usando essa fórmula pra 0 a 10 segundos temos:

Agora vamos ver de 30 segundos a 40 segundos! Em 30 segundos a velocidade ainda é 16,67 m/s e nos 40 segundos a velocidade é 0, então a gente já pode usar a fórmula da aceleração média:

De 10s até 30s, a velocidade é de 16,67 m/s para os dois, então temos a seguinte aceleração:

Agora ele quer saber de 0 a 40 segundos. Sabendo que a velocidade em 0 segundos e em 40 segundos é nula, a aceleração média nesse tempo também será 0 m/s².

Bora pra letra b)!!!