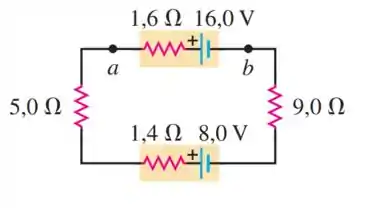
O circuito elétrico indicado na Figura E25.33 contém duas baterias cada uma com uma fem e uma resistência interna, e dois resistores. Calcule (a) a corrente no circuito (modulo e sentido) e (b) a voltagem nos terminais da bateria de .
Passo 1
Olá, tudo bem? Vou te ajudar a resolver essa atividade.
Aqui temos o seguinte circuito para analisarmos:
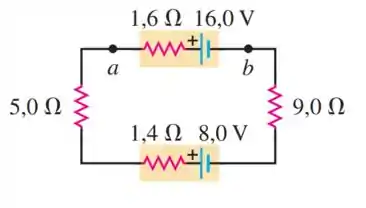
Para resolver este problema de circuito, vamos usar a Regra das Malhas de Kirchhoff.
O circuito é composto por uma única malha, e isso facilita o nosso trabalho. A corrente no circuito é a mesma em todos os pontos, já que é uma única malha. Vamos supor um sentido para a corrente, digamos, o sentido horário (). Se o valor final de for positivo, o sentido assumido está correto; se for negativo, o sentido real é o anti-horário.
Passo 2
- Aplicando a Regra das Malhas no sentido horário, partindo do ponto :
A soma das variações de potencial em uma malha fechada é zero:
Agrupando os termos:
Substituindo os valores:
Como o valor de é positivo, o sentido da corrente é o que assumimos, ou seja, horário.
Passo 3
A voltagem é a diferença de potencial entre os terminais e . Para a bateria superior (de ), o potencial em () é maior que o potencial em (), pois o ponto está conectado à placa positiva (terminal de maior potencial) e o ponto está conectado à placa negativa (terminal de menor potencial).
A bateria está fornecendo energia, pois a corrente () sai do terminal positivo. A voltagem nos terminais de uma bateria real que fornece corrente é dada por:
Neste caso, a voltagem é
O problema pede , que é
Organizando:
Portanto: