7.3P Determine a posição do centro de massa do hemisfério homogêneo de raio , visto na Figura 7.13.
Passo 1
Show de belezeras galerinha, nosso hemisfério homogêneo é dado na figura como a parte inferior de uma esfera:
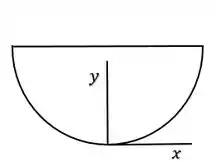
Iradoso, e pra começar, podemos ver que o eixo divide o hemisfério exatamente no meio, isso quer dizer que como estamos tratando de um hemisfério homogêneo, o centro de massa vai estar nesta mesma linha do eixo , ou seja, já podemos garantir que no eixo , o centro de massa estará no ponto :
Passo 2
Xuxu beleza, mas agora que vem a parte legal, porque precisamos encontrar em que ponto do eixo a coordenada do centro de massa se encontre. E se tratando de um sólido homogêneo, temos que a equação que descreve a posição do centro de massa é:

Onde é a massa total do sólido. Mas calma lá meu patrão, porque nesse caso precisamos fazer uma alteração das variavies, precisamos sair da varialvel e ir para outra mais conhecida. E pra isso podemos lembrar que a massa e o volume de um sólido homogêneo se relacionam através da densidade de cada sólido:
Tal que nossa massa é:
Então se a gente for pro infinitesimal, teremos que um infitésimo de massa será o equivalente a um infitésimo de volume :
E substituindo isso na nossa integral, temos:
E se a gente cortar o , teremos que:
Passo 3
Feshow de bola, agora colocamos nosssa integral em função de uma variavel que a gente conhece melhor. O volume de um hemisfério, vai ser exatamente a metade do volume de uma esfera, e dado que nossa hemisfério possui uma raio , temos:
Mass agora para o termo infinitesimal , vamos ter que usar da malandragem. Saca só, queremos definir o termo infinitesimal de volume , mas como estamos trabalhando com a variavel , seria sensacional se pudessemos relacionar esse termo com nossa variavel . Então o que a gente pode fazer é imaginar que a gente dividiu nossa hemisfério em vários discos de raio :
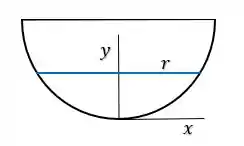
Cada disco desse vai possuir uma área dada por:
Maaaasss, se a gente disser que esse disco possui uma altura infinitesimal :
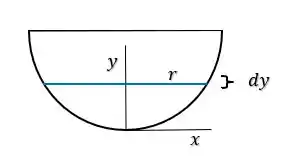
Poderemos então, dizer que ele vai possuir um volume infinitesimal tal que:
Belejóia, então de forma bem sagz conseguimos sair do infitesimal e ir para , o que é beeeemmm melhor pra gente. Nossa integral agora é:

Passo 4
Bora que ta acabando galerinha. Ta vendo quele termo na nossa integral, então, não conhecemos ele, não sabemos nada dele, onde ele vive, o que ele come o que ele faz nas horas vagas. Então se a gente não sabe nada dele, vamos colocar ele em função de alguma variavel que a gente conhece. Saca só, se a gente montar um trinagulo com esse raio e o raio teremos:
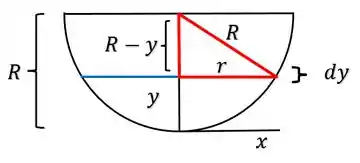
Sendo assim, o raio será:
Logo:
Dessa forma nossa integral pode ser reescrita como:
E como nosso hemisfério vai de até , temos que nossa posição do centro de massa será dada por:
E finalmente resolvendo essa integral, descobrimos que:
Portano:
