Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 6.Exercícios e Problemas - Ex. 19
6.19P Uma pequena pastilha partindo do repouso do topo de uma esfera desliza sem atrito sobre a mesma (Figura 6.16). A) Identifique as forças que atuam sobre a pastilha enquanto ela mantém contato com a esfera. B) Determine a variação da velocidade da partícula com o ângulo , antes de a partícula perder contato com a esfera. C) Calcule o valor no qual a pastilha perde contato com a esfera. Sugestão: determine o ponto em que a trajetória da partícula ainda é circular mas a força entre a pastilha e a esfera é nula.
Passo 1
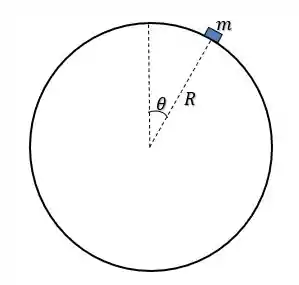
Show de bolinhas meus amores, a figura 6.16 é a seguinte:
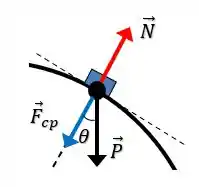
Na letra (A) ele quer a gente escreva as forças que estão atuando sobre nosso bloco de massa através de um diagrama de forças. MAAAASSS o enunciado nos deu a brilhante sugestão de levar em conta que durante o contato com a esfera a nossa trajetória é circular.
Perai chefe, porque se nossa trajetória é circular, quer dizer que além das forças peso e normal, existe uma força centrípeta atuando sobre o nosso bloco, tal que o diagrama de forças é:
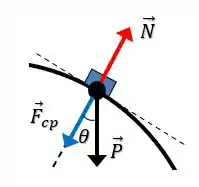
Onde e são as forças peso e normal respectivamente. E a força centrípeta sempre vai apontar para o centro da trajetória.
Passo 2
Iradoso, agora na letra (B) queremos encontrar a variação de velocidade com o ângulo de até o bloco perder contato com a esfera. MAAASSS o bizu master de todos os tempos aqui, é que o bloco vai perder o contato com a esfera quando a força normal estiver na iminência de se igualar a força centrípeta.
Porque nesse momento, as forças que atuam nesse eixo irão se anular e, portanto, não haverá nenhuma força mantendo a bloco sobre a esfera, a resultante nesse eixo será nula. Dito isso, a força centrípeta sobre um corpo qualquer é dada como:
Onde é a massa do bloco, é a velocidade em que ele se encontra, e é o raio da trajetória circular. Além disso a força normal é uma reação a força peso, nesse caso deve ser perpendicular a trajetória tal que:
Sendo assim, nossa igualdade de forças se torna:
Portanto a velocidade final no ponto onde o bloco perde o contato com a esfera é:
E já que o bloco parte do repouso, temos que a velocidade inicial logo a variação da velocidade nesse intervalo de tempo será:
Passo 3
Belezera, agora que vem a melhor parte da brincadeira. O enunciado quer que a gente encontre o ângulo onde o bloco perde contato com a esfera
Calma lá, vamos com carinho. A malandragem aqui, é que podemos usar a conservação da energia mecânica, isto é, a energia mecânica inicial do nosso sistema vai ser exatamente igual a energia mecânica final do nosso mesmo sistema:
A energia mecânica inicial possui somente energia potencial gravitacional que o bloco possui no topo da esfera, dada pela altura do raio:
Já a energia mecânica final, vai ser uma mistura de energia cinética (devido a velocidade adquirida durante a queda) e de energia potencial gravitacional (já que o bloco ainda possui uma altura no momento da separação), dessa forma:
A energia cinética é dada pela fórmula , enquanto a altura final da energia gravitacional será , tal que:
E como na letra (B) descobrimos a velocidade final nesse ponto, , obtemos que:
E então se a gente igualar essas energias final e inicial que encontramos, descobrimos que:
Portanto, se tirarmos o valor numa calculadora, teremos que o ângulo que corresponde ao momento em que o bloco perde contato com a esfera é:
