Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 74

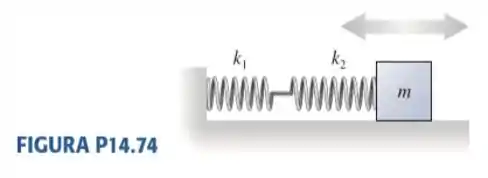
74. Sobre uma mesa sem atrito, um bloco está preso entre duas molas de constantes elásticas k 1 e k 2 , como mostra a FIGURA P14.74. Obtenha uma expressão para a frequência de oscilação f   do bloco em função das freqüências f 1 e f 2 com as quais ele oscilaria se estivesse preso somente à mola 1 ou à mola 2 .

Passo 1

Opa! Hey brother! Bora pra mais uma questãozinha sobre Ondulatória!

E a primeira coisa a se fazer pra resolver esse problema, já sabe né? Bora fazer o diagrama de corpo livre, indicando as forças atuantes em nosso bloco!

E obtemos assim, a seguinte imagem:

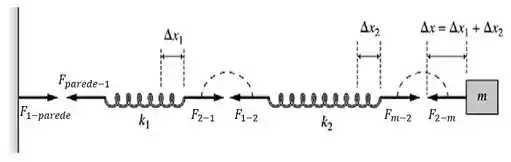
Por ela, sabemos que a força atuante sobre a massa, é na verdade a força F 2 - m .

Só que essa força F 2 - m , pela mola 2 , sabemos que é igual a...

F 2 - m = F 1 - 2

E pela mola 1 , também tiramos que...

F 1 - 2 = F 2 - 1 = F p a r e d e - 1

Sendo assim, temos que...

F 2 - m = F 1 - 2 = F 2 - 1

F 2 - m = k 1 ∆ x 1 = k 2 ∆ x 2

Passo 2

Bom! Como temos uma associação de molas em série, então...

∆ x = ∆ x 1 + ∆ x 2

O deslocamento total da mola equivalente da associação, é a soma dos deslocamento das outras duas molas... Desse modo;

∆ x = ∆ x 1 + ∆ x 2

∆ x = F 2 - m k 1 + F 2 - m   k 2

∆ x = 1 k 1 + 1 k 2 F 2 - m  

∆ x = k 1 k 2 k 1 k 2 F 2 - m  

Essa expressãozinha aí k 1 + k 2 k 1 k 2 , é nada mais nada menos do que a contante de mola equivalente, k e q :

∆ x = k 1 k 2 k 1 + k 2 F 2 - m  

∆ x = k e q F 2 - m  

Passo 3

Sendo assim, pegando a fórmula da frequência angular para o sistema massa-mola...

ω = k m

Mas como no caso, subsituimos todo o nosso sistema anterior com duas molas e uma massa, por um sistema com uma massa e uma constante de mola equivalente; então...

ω = k e q m

ω = 1 m ⋅ k 1 k 2 ( k 1 + k 2 )

Dividindo por m no numerador e no demominador...

ω = 1 m ⋅ k 1 k 2 ( k 1 + k 2 )

ω = 1 m ⋅ k 1 m ⋅ k 2 m k 1 m + k 2 m

Como as frequências angulares ω das molas 1 e 2 são...

ω 1 = k 1 m

ω 2 = k 2 m

Então...

ω 1 2 = k 1 m

ω 2 2 = k 2 m

E ficamos finalmente, com...

ω = 1 m ω 1 2 ⋅ ω 2 2 ω 1 2 + ω 2 2

ω = 1 m ω 1 2 ⋅ ω 2 2 ω 1 2 + ω 2 2

Onde sabendo da seguinte relação...

ω = 2 π f

Ou seja, ω e f estão relacionados por apenas uma constante, que no caos iremos desprezar, então...

f = f 1 2 ⋅ f 2 2 f 1 2 + f 2 2

É claro que isso é a expressão fundamental! No caso ignoramos completamente o 1 m e a constante 2 π , pois no caso, ambas resultariam em constantes que multiplicariam toda a expressão...

Resposta

f = f 1 2 ⋅ f 2 2 f 1 2 + f 2 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na figura, duas molas iguais, de constante elástica 7580N / m , estão ligadas a um bloco de massa 0,245k g . Qual é a frequência de oscilação no piso sem atrito?
Com um bloco de massa m e duas molas, de constantes elásticas k 1 e k 2 , montam-se dois arranjos indicados nas Figuras (a) e (b). Calcule as respectivas frequências angular ω a e ω b de pequenas osci
97. A constante elástica efetiva de duas molas. Duas molas, ambas com o mesmo comprimento sem deformação, porém com constantes diferentes k 1 e k 2 , são ligadas a um bloco de massa m apoiado sobre um
73. Sobre uma mesa sem atrito, um bloco está preso entre duas molas de constantes elásticas k 1 e k 2 , como mostra a FIGURA P14.73. Demonstre que a freqüência de oscilação do bloco é determinada por