Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 11.1 - Ex. 100
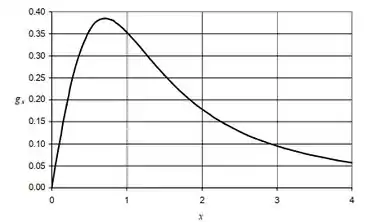
(a) Um anel fino e homogêneo, de massa e raio , está no plano e centrado na origem. Esboce o gráfico do campo gravitacional , versus para todos os pontos no eixo . (b) Em qual ponto, ou quais pontos, a magnitude de é máxima?
Passo 1
a) Para esboçar o gráfico do campo em relação a , a gente precisa da função . Vamos tentar encontra-la a partir dos dados do problema.
Primeiramente, vamos considerar um pedaço bem pequeno do anel com comprimento e massa . Olha essa ilustração aqui embaixo:
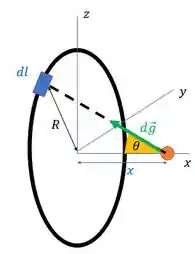
Queremos equacionar o campo causado por no ponto marcado de laranja, que dista da origem. A fórmula vai ser análoga a fórmulinha de um campo causado por uma massa
é a distância entre o pedaço e o ponto sobre o eixo . Para acharmos a distância entre nosso pedaço de anel e o eixo, podemos usar o teorema de Pitágoras. Isso porque (que está contido no plano ) é perpendicular a . Ficamos assim:
Nosso campo vai ficar assim:
Agora vamos achar . A densidade linear do anel como todo pode ser encontrada pela divisão entre a massa total do anel e a o comprimento do anel. Já que ele é circular, o comprimento é , então a densidade fica
Assim, a gente consegue achar uma relação entre e :
Substitiundo no nosso campo
Passo 2
Lembrando que queremos saber o campo resultante sobre os pontos do eixo .
Repare que o campo resultante só vai ter componente . Por que? Imagina que a gente tem dois pedaços . Um na parte mais alta do anel e outra na mais baixa:
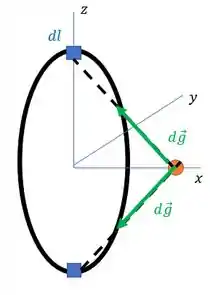
As componentes verticais dos dois vão se anular, ficando apenas a componente em . Como a massa do anel está posicionada com uma simetria em relação a , isso acontece em todas as direções, fazendo com que o campo resultante fique apenas na direção .
Então vamos decompor nossa expressão de em :
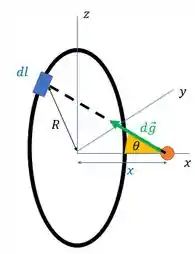
Fica:
Da figura, temos um triângulo retângulo dado por , o ponto laranja e a origem dos eixos. Assim o cateto oposto de é , o adjacente é , a hipotenusa (por pitagoras) é . Logo:
Voltando na componente do campo
Passo 3
Como
Agora vamos integrar para achar o campo resultante causado por todo o anel. Como a variável da nossa integral é (o comprimento), vamos integrar de até o comprimento total do anel :
Tirando o que não depende de da integral:
Portanto,
O gráfico vai ficar assim:
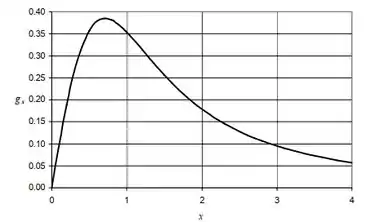
Podemos interpretar que essa distribuição é simétrica em relação a origem. Ou seja, em um ponto onde temos negativo, o campo tem o mesmo módulo, mas sinal trocado (Sentido oposto).
Passo 4
(b) Para acharmos o ponto de máximo, vamos derivar a expressão do campo e igualar a zero.
Derivando,
Usamos a regra do quociente aqui em cima!
Simplificando o fator :
Portanto,
Pelo gráfico do item (a), vemos que a curva possui concavidade para baixo. Assim, podemos concluir que esses são pontos de máximo.
Resposta
O gráfico vai ficar assim:
