Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.5 - Ex. 44
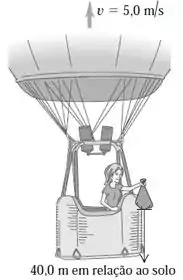
Um balonista de ar quente que se desloca verticalmente para cima com velocidade constante de módulo igual a deixa cair um saco de areia no momento em que ele está a uma distância de acima do solo (Figura 2.41). Após ser largado, o saco de areia, passa a se mover em queda livre.
a) Calcule a posição e a velocidade do saco de areia e depois de ser largado.
b) Calcule o tempo que o saco de areia leva para atingir o solo desde o momento em que ele foi lançado.
c) Qual é a velocidade do saco de areia quando ele atinge o solo?
d) Qual é a altura máxima em relação ao solo atingida pelo saco de areia?
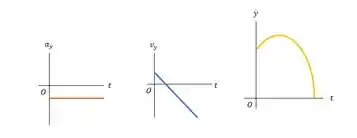
e) Faça gráficos , e para o movimento do saco de areia.
Passo 1
Opa, aqui temos um balão subindo com velocidade constante de e quando a altura do balão em relação ao solo é a pessoa que tá dentro do balão deixa cair um saco de areia!
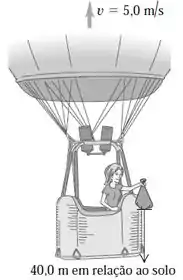
Sim, tadinha da pessoa que tiver em baixo do balão! Mas vamos ao que interessa...A primeira coisa que queremos saber é a posição e a velocidade do saco de areia e depois de ser largado.
Vamos analisar o problema:
Quando ele larga o saco de areia, como o balão está subindo com velocidade , o saco cheio de areia inicialmente terá essa mesma velocidade, nesse mesmo sentido.
Vamos fazer uma recordação: pela Lei da Inércia “um corpo que está se movendo tende a continuar se movendo, até que a resultante das forças atuando sobre ele não seja nula”.
Lembra o que acontece quando alguém freia bruscamente, e o carona é arremessado para frente? No caso, o saco tende a continuar subindo a , porém a gravidade vai começar a atuar sobre ele, retardando o movimento de subida.
Então, ele faz um lançamento vertical para cima.
Além disso, ele é largado de 40m de altura, sendo essa sua posição inicial.
Passo 2
O item (a) pede a posição e a velocidade do saco em t = 0,250s e em t = 1s em, basta usarmos as equações da posição do movimento uniformemente variado:
A equação é:
Substituindo os dados e aplicando :
Note que achamos um valor mais alto que a posição inicial.
Passo 3
Vamos refazer o último passo, mas para :
Passo 4
Vamos agora calcular a velocidade de cada tempo do item (a) usando a equação:
Para :
Passo 5
Para :
Passo 6
Item (b)
Para descobrir o tempo em que o saco chega ao solo, temos que encontrar o tempo quando . Para isso vamos usar a equação da posição pelo tempo.
Substituindo os valores encontrados temos:
Resolvendo a equação de segundo grau:
O tempo não é negativo, e por isso, vamos ignorar quando ele for menor que zero. Assim, a resposta do item é:
Passo 7
Para encontrar a velocidade com que o saco atinge o solo , podemos usar tanto a equação da velocidade pelo tempo, como a equação de Torricelli.
Para facilitar nossos cálculos, vamos usar, a equação de Torricelli:
Temos todos os dados para descobrir a velocidade do saco:
Como ele pede a velocidade, é importante mostrar qual o sentido dela: ao chegar ao chão, o saco de areia estará caindo, então sua velocidade é para baixo, portanto, negativa.
Passo 8
A altura máxima acontece quando a velocidade é zero. Como o enunciado não forneceu o tempo onde isso acontece, podemos usar a equação de Torricelli:
Passo 9
Sabemos que a aceleração é a aceleração da gravidade que é constante e negativa.
Para fazer o gráfico da velocidade note que o saco de areia inicialmente viaja para cima com velocidade decrescente e depois se move para baixo com velocidade crescente.
Sabemos que o gráfico da posição é uma parábola por se tratar de um movimento uniformemente variado. Repare que assim como comentamos, o saco começa subindo até ter sua velocidade igual a zero e então ele começa a descer.
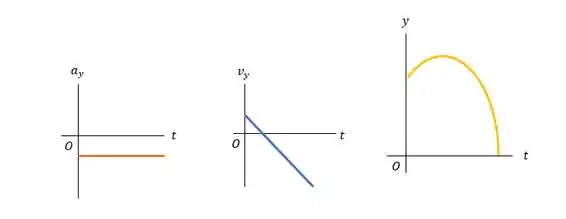
Resposta
- Para : e ;
Para : e .
