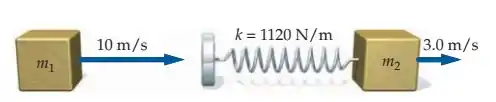
Um bloco de massa desliza sobre uma mesa sem atrito com uma rapidez de . Diretamente à frente dele e se deslocando no mesmo sentido com uma rapidez de , está um bloco de massa . Uma mola sem massa, de constante de força , está presa ao segundo bloco, como na Figura 8-47. (a) Qual é a velocidade do centro de massa do sistema? (b) Durante a colisão, a mola sofre uma compressão máxima . Qual é o valor de ? (c) Os blocos acabarão por se separar novamente. Quais são as velocidades dos dois blocos, após a separação, medidas no referencial da mesa?

A gente quer a velocidade do centro de massa do sistema formado pelos dois blocos (a mola não tem massa, aí a gente não usa ela aqui). Como não há menção de forças externas sobre eles, a gente pode usar a lei da conservação de quantidade de movimento:

Onde é a massa total do sistema, ou seja, a soma das massas de cada bloco:

representa a soma das quantidades de movimento de cada bloco. A quantidade de movimento é dada por , então essa soma para o nosso caso fica:

E é a velocidade do centro de massa do sistema que gente quer achar. Então vamos substituir e na lei da conservação:

Isolando

Substituindo os valores do enunciado:

b) Agora, vamos lá. Para calcular a compressão da mola, vamos usar a equação de conservação de energia. A energia mecânica de um objeto é dada por

A energia potencial gravitacional não vai ter influencia aqui na nossa situação porque não há mudanças de altura. Mas como há velocidade e uma mola, vamos analisar a energia potencial elástica e a energia cinética dos objetos .

Como não há forças externas e nem forças dissipativas (tipo, não há atrito), a conservação de energia diz que

Onde o nosso primeiro momento vai ser quando os blocos estão separados. Nesse momento a mola está frouxa, então só há energia cinética, que é a soma das energias de cada bloco:

No final, o bloco 1 está pressionando a mola na sua deformação máxima. Eles continuam se movimento, então há velocidade e deformação da mola, então há energia cinética e energia potencial elástica:

Só que a energia cinética é pode ser dividida assim:

Ou seja, é a soma das energias cinéticas do bloco em relação ao centro de massa e a energia do centro de massa do sistema. Essa última nunca varia porque não temos forças externas.

Maaas uma dessas energias precisa ser totalmente consumida para colocar a mola na deformação máxima. Quem vai ser? A soma das energias cinéticas relativas! Porque elas podem variar.

Então se toda essa energia dos blocos relativa ao centro de massa vira energia potencial elástica que se traduz na deformação na mola, a energia mecânica no momento onde há deformação máxima (e há a menor distância entre blocos), vai ser:

Que é a soma de energia potencial elástica e a energia cinética do centro de massa. Essa última é calculada normalmente, só que a velocidade vai ser e a massa é a massa total do sistema. Vamos então substituir as expressões de cada energia ali:

Igualando a energia no início e fim:

Isolando quem a gente quer:

c) Cara, agora a gente quer as velocidades dos blocos depois que eles sem encontram e se separam.

Como não há forças externas, a gente pode usar a conservação de quantidade de movimento:

Sendo que . A quantidade de momento do sistema é a soma das quantidades de cada bloco, então nossa conservação fica:

No momento inicial a gente já tem as velocidades, e temos também as massas de cada bloco, então podemos substituir:

Só que a gente não tem nenhuma das duas velocidades finais dos blocos e depois que eles se separam. O que a gente faz?

Vamos precisar de mais uma equação! Aí a gente forma um sistema. Como não temos forças dissipativas, a gente pode dizer que a colisão é elástica. Esse tipo de colisão tem coeficiente de restituição de .

O coeficiente de restituição tem essa fórmulinha:

Substituindo o que a gente tem:

Substituindo na equação do passo anterior:

Voltando para achar :