Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 28.1 - Ex. 80

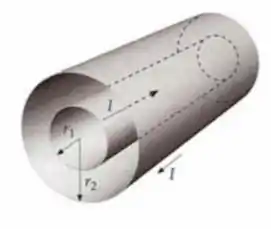
Um cabo coaxial consiste em dois condutores cilíndricos de paredes muito finas com raios r 1 e r 2 (Figura 28-62). As correntes nos cilindros interno e externo são iguais em magnitude mas têm sentidos opostos.

a Use a lei de Ampère para determinar o campo magnético como função da distância perpendicular r do eixo central do cabo para 1   0 < r < r 1 , 2 r 1 < r < r 3 e 3   r > r 2 .

( b ) Mostre que a densidade de energia magnética na região entre os cilindros é dada por u m = 1 2 ⋅ μ 0 4 π ⋅ I 2 π r 2

c Mostre que a energia magnética total no volume de um cabo de comprimento l é dada por U = μ 0 4 π ⋅ I 2   l ⋅ ln ⁡ r 2 r 1 .

d Use o resultado da parte c e a relação entre a energia magnética, corrente e indutância para mostrar que a auto indutância por unidade de comprimento da disposição do cabo é dada por L l = μ 0 2 π ⋅ ln ⁡ r 2 r 1 .

Passo 1

E aí bonit@s, tudo bem com vocês?

Se liga só no que vamos utilizar pra fazer essa questão o sistema exibe simetria cilíndrica, então pode-se usar a lei de Ampère para determinar B dentro do cilindro interno, entre os cilindros e fora do cilindro externo. Podemos usar

u m = B 2 2 μ 0

e a expressão para B da Parte ( a ) para expressar a densidade de energia magnética na região entre os cilindros. Podemos integrar esta expressão para um sobre o volume entre os cilindros para encontrar a energia magnética total em um volume de comprimento l . Finalmente, podemos usar nosso resultado na Parte ( c ) U m = L I 2 2 para encontrar a auto-indutância dos cilindros por unidade de comprimento.

Passo 2

Para r < r 1   e   r > r 2 a corrente encerrada líquida é zero, consequentemente, nestas regiões:

B r < r 1 = 0   e   B r > r 2 = 0

Agora pra r 1 < r < r 2 teremos

2 π r B = μ 0 I c → B r 1 < r < r 2 = μ 0 I 2 π r

Passo 3

Expressando a densidade de energia magnética na região entre os cilindros vamos encontrar

u m = B 2 2 μ 0

Substituindo nosso valor de B encontrado no item anterior vamos encontrar

u m = μ 0 I 2 π r 2 2 μ 0

Simplificando nossa expressão vamos encontrar

u m = μ 0 I 2 8 π 2 r 2

Passo 4

Agora, vamos expressar a energia magnética d U m no elemento cilíndrico de volume d V :

d U m = u m d V = μ 0 I 2 8 π 2 r 2 ⋅ l 2 π r   d r = μ 0 I 2 l 4 π ⋅ d r r

Integrando ambos os lados de r 1 até r 2 vamos encontrar

U m = μ 0 I 2 l 4 π ⋅ ∫ r 1 r 2 d r r = μ 0 I 2 l 4 π ⋅ ln ⁡ r 2 r 1  

Passo 5

Por fim, para finalizarmos o problema vamos expressar a energia no campo magnético em termos de L e I , assim, obteremos

U m = 1 2 ⋅ L I 2 → L = 2 U m I 2

Do item anterior temos que

U m I 2 = μ 0 l 4 π ⋅ ln ⁡ r 2 r 1

Substituindo vamos encontrar

L = 2 ⋅ μ 0 l 4 π ⋅ ln ⁡ r 2 r 1 = μ 0 l 2 π ⋅ ln ⁡ r 2 r 1

Expressando o raio vamos encontrar

L l = μ 0 2 π ⋅ ln ⁡ r 2 r 1

Pronto, tá finalizado nosso problema.

Resposta

D e m o n s t r a ç ã o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma antena em forma de espira, com uma área de 2,00c m 2 e uma resistência de 5,21μ Ω , é mantida perpendicular a um campo magnético uniforme de módulo 17,0μ T . O módulo do campo magnético diminui pa
Na Fig. 30-53, uma espira retangular muito longa, de largura L , resistência R e massa m , está inicialmente suspensa na presença de um campo magnético horizontal uniforme B → orientado para dentro do
Se 50,0c m de um fio de cobre com 1,00m m de diâmetro são usados para formar uma espira circular, que é mantida perpendicular a uma campo magnético uniforme que está aumentando a uma taxa constante de
Na Fig. 30-51a, uma espira circular é concêntrica com um solenoide e está em um plano perpendicular ao eixo central do solenoide. A espira tem 6,00c m de raio. O solenoide tem um raio de 2,00c m , pos
Um solenoide longo tem um diâmetro de 12,6c m . Quando a corrente i percorre as espiras, um campo magnético B = 28,6 m T é gerado em seu interior. Diminuindo i , o campo decresce a uma taxa de 6,51 m