Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 28.Exercícios e Problemas - Ex. 56

Um cilindro infinito longo e de raio R apresenta uma densidade linear de carga λ . A densidade volumétrica de carga (em C / m 3 ) no interior do cilindro ( r ≤ R ) é dada por ρ r = r ρ 0 / R , onde p 0 é uma constante a ser determinada.

a. Desenhe o gráfico de ρ versus x considerando que o eixo x cruze o cilindro pelo centro e seja perpendicular ao eixo do mesmo. O gráfico deve mostrar x variando desde - 2 R até + 2 R .

b. A carga contida em um volume infinitesimal dV é d q = ρ d V . A integral de ρ d V sobre o cilindro de comprimento L é igual à carga total Q = λ L do cilindro. Use este fato para mostrar que ρ 0 = 3 λ 2 π R 2 .

Dica: Considere dV como o volume infinitesimal de uma casca cilíndrica de comprimento L, raio r e espessura dr. Qual é o volume de uma casca como essa?

c. Use a lei de Gauss para obter uma expressão para o campo elétrico E no interior do cilindro, r ≤ R .

d. Sua expressão fornece o valor esperado na superfície, r = R ? Explique.

Passo 1

Vamos entender como deve ser este gráfico. No ponto x = 0 ρ 0 será nulo, e vai crescer linearmente até R e - R pontos em que ρ 0 atinge seu valor máximo. Fora do raio temos que ρ 0 = 0

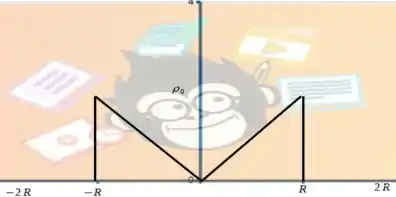
Passo 2

A questão nos disse que

ρ r = r ρ 0 / R

Como

d q = ρ d V

Temos o seguinte

d q = r ρ 0 R 2 π r L d r

d q = ρ 0 L 2 π R r 2 d r

Já encontramos a expressão para uma carga infinitesimal, agora vamos encontrar a carga para o cilindro.

Q = ∫ d q

Q = ρ 0 L 2 π R r 3 3

Como estamos integrando de 0 a R

Q = ρ 0 L 2 π R R 3 3

Também sabemos que Q = λ L

ρ 0 L 2 π R R 3 3 = λ L

Isolando ρ 0

ρ 0 = 3 λ 2 π R 2

Passo 3

Pela Lei de Gauss

Φ e = A E = Q i n t ε 0

Porém, no Passo 2 determinamos a carga

Q = ρ 0 L 2 π R r 3 3

Podemos substituir ρ 0 pela resposta do item b. Então teremos

Q = L 2 π R r 3 3 ⋅ 3 λ 2 π R 2

Fazendo algumas simplificações

Q = λ L ⋅ r 3 R 3

Vamos substituir essa informação na Lei de Gauss

A E = λ L ⋅ r 3 ε 0 R 3

Vamos adicionar a área do cilindro

2 π r L E = λ L ⋅ r 3 ε 0 R 3

Logo

E = λ 2 π ε 0 ⋅ r 2 R 3

Passo 4

Como a equação do Passo 3 vale para r ≤ R , só precisamos igualar r = R

E = λ 2 π ε 0 ⋅ r 2 R 3

Substituindo

E = λ 2 π ε 0 R

Este é um valor previsto para o caso de um cilindro com campo pelas laterais.

Resposta

a.

Resposta no Passo 1

b.

ρ 0 = 3 λ 2 π R 2

c.

E = λ 2 π ε 0 ⋅ r 2 R 3

d.

E = λ 2 π ε 0 R

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma distribuição de carga esfericamente simétrica, não-uniforme, produz um campo elétrico de módulo E = K r 4 ,orientado radialmente para fora da esfera. Na expressão, r é a distância ao centro da esf
Uma carga + q colocada a uma distância a de um plano condutor infinito, induz carga sobre o plano com uma densidade superficial σ = - q a /( 2 π r 3 ) , onde r é a distância da carga + q até um ponto
Num modelo antigo do átomo de hidrogénio, a carga + e do próton está uniformemente distribuída sobre uma esfera de raio a 0 , tendo em seu centro o elétron de carga - e e massa m . (a) Se o elétron fo
Quando uma esfera metálica, eletricamente neutra, de raio a , está imersa num campo elétrico uniforme de módulo E , encontra-se que a densidade superficial de carga induzida sobre a esfera é σ = 3 ϵ 0
(a) Para a situação do Problema 60, qual é a força eletrostática entre a carga + q e a carga induzida sobre o plano condutor? Ela é atrativa ou repulsiva? (b) Que carga, colocada na posição simétrica