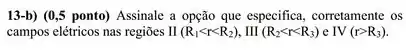Exercícios de Lei de Gauss – Simetrias - Lista de Exercícios Resolvida
Questão 1
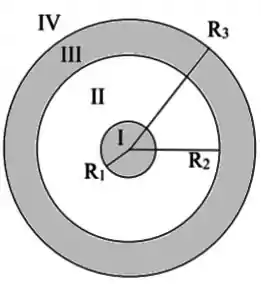
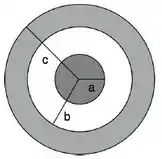
Um fio finito muito longo de comprimento e carregado com uma carga está no eixo de um cano cilíndrico condutor descarregado de raio interno , raio externo e mesmo comprimento .
Que cargas aparecem nas superfícies interna e externa do cano?
Utilize a Lei de Gauss para calcular o vetor campo elétrico para , e ;
Ver solução completaQuestão 2
Suponha que você segure duas grandes folhas de plástico frente à frente, espaçadas uma da outra por , conforme mostra a figura. Atritando uma delas com lã e a outra com seda, você consegue obter, sobre a superfície de uma das folhas, uma densidade superficial uniforme de carga , e sobre a outra, outra densidade superficial uniforme de carga . Qual o vetor campo elétrico nos pontos , e ?
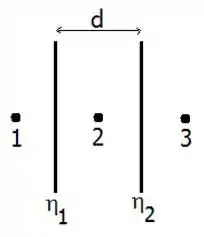
Questão 3
Determine o campo elétrico produzido por um plano infinito com uma distribuição de carga uniforme positiva por unidade de área igual à .
Ver solução completaQuestão 4
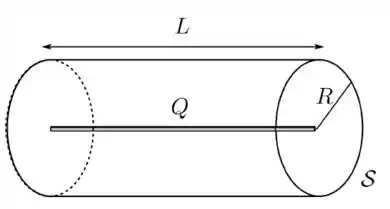
A figura a seguir é uma seção de uma barra condutora de raio e comprimento no interior de uma casca coaxial, de paredes finas, de raio e mesmo comprimento .
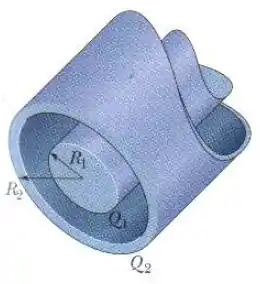
A carga da barra é ; a carga da casca é . Determine:
- O módulo do campo elétrico a uma distância radial ;
- A direção (para dentro ou para fora) do campo elétrico a uma distância radial ;
- O módulo do campo elétrico a uma distância radial
- A direção (para dentro ou para fora) do campo elétrico a uma distância radial ;
- A carga na superfície interna da casca;
- A carga na superfície externa da casca;
Questão 5
Encontre o vetor campo elétrico de uma carga pontual à uma distância dela.
Ver solução completaQuestão 6
Calcule a expressão para o vetor campo elétrico na região fora de uma esfera carregada com densidade volumétrica de carga :
Onde é a distância de um ponto até a origem e .
A esfera tem raio e é uma constante.
Ver solução completaQuestão 7
Calcule a expressão para o vetor campo elétrico na região dentro de uma esfera carregada com densidade volumétrica de carga :
A esfera tem raio .
Ver solução completaQuestão 8
Uma pequena esfera oca condutora, com raio interno e externo , é concêntrica com uma grande esfera oca condutora, com raio interno e raio externo , conforme a figura abaixo. A carga total sobre a esfera oca interna é igual à e a carga total sobre a esfera oca externa é igual à . Determine o módulo, direção e sentido do campo elétrico em função da distância ao centro comum para as regiões:
E qual a carga total sobre (i) a superfície interna da esfera oca pequena; (ii) a superfície externa da esfera oca pequena; (iii) a superfície interna da esfera oca grande; (iv) a superfície externa da esfera oca grande?
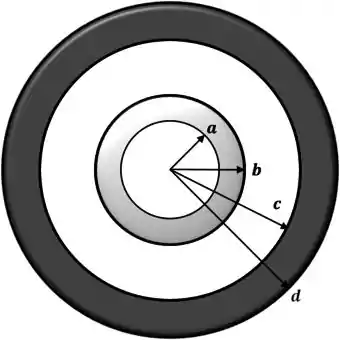
Questão 9
A figura mostra, em seção reta, duas esferas de raio , com distribuições volumétricas uniformes das cargas. O ponto está sobre a reta que liga os centros das esferas, a uma distância do centro da esfera . Se o campo elétrico no ponto é igual a zero, qual é a razão entre a carga da esfera e a carga da esfera ?
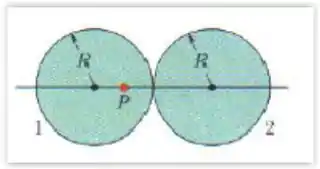
Questão 10
Uma placa isolante, com espessura e densidade volumétrica de carga uniforme igual a , está separada de uma outra placa, condutora, com carga total igual a zero e de espessura . As duas placas são infinitas nas direções e , conforme a figura.
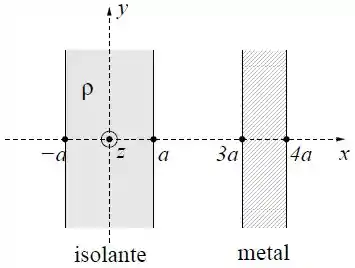
Use a lei de Gauss para calcular o vetor campo elétrico produzido pela placa isolante em um ponto dentro da placa, isto é um ponto com coordenada .
Use a lei de Gauss para calcular o vetor campo elétrico produzido pela placa isolante em um ponto fora dela.
Calcule, em termos de e , a densidade superficial de cargas induzidas nas superfícies da placa condutora após o equilíbrio eletrostático ter sido atingido. Determine em todo o espaço o campo elétrico resultante devido ao isolante e ao condutor.
Ver solução completaQuestão 11
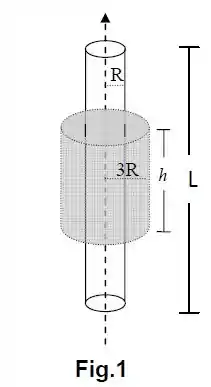
Um bastão cilíndrico isolante, de comprimento e raio (com ), foi carregado uniformemente em sua superfície com carga negativa desconhecida (Figura 1). Mediu-se o campo elétrico gerado a uma distância do eixo de simetria e encontrou-se o valor (em módulo).
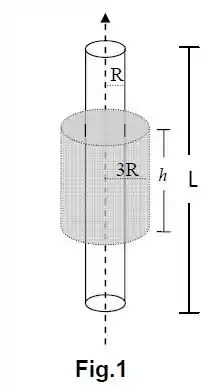
Calcule o fluxo do campo elétrico através da superfície indicada (sombreada) na Figura 1 (altura e raio ).
Obtenha o vetor campo elétrico em função da distância ao eixo do bastão, para .
Suponha agora que uma casca cilíndrica condutora descarregada (neutra) de comprimento e raios interno e externo é colocada em volta do bastão carregado utilizando-se luva de borracha. Posiciona-se a casca com o eixo de simetria coincidindo com o eixo do bastão (concêntrico), conforme a Figura 2.
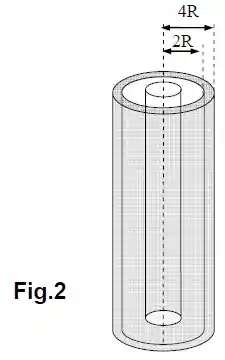
Responda, justificando:
Obtenha o valor (módulo) do campo elétrico à distância do eixo.
Quanto vale a carga na superfície interna e na superfície externa da casca cilíndrica?
Agora suponha que a casca cilíndrica condutora seja aterrada. Responda, justificando:
Quanto vale a carga na superfície interna e na superfície externa da casca cilíndrica?
Calcule o fluxo elétrico que atravessa uma superfície cilíndrica concêntrica ao sistema e de raio .
Ver solução completaQuestão 12
A figura mostra as seções retas de duas placas de grande extensão, paralelas, não-condutoras, positivamente carregadas, ambas com distribuição superficial de cargas .
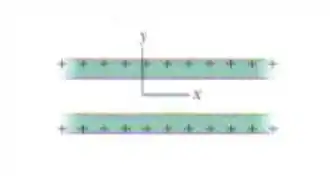
Determine o campo elétrico em termos dos vetores unitários.
(a) Acima das placas;
(b) Entre as placas;
(c) Abaixo das placas;
Ver solução completaQuestão 13
Um cilindro carregado muito longo, de raio , possui uma densidade linear de carga . Determine o campo elétrico criado pelo cilindro:
Fora do mesmo, para .
Dentro do cilindro, para .
Mostre também que suas respostas coincidem na borda do cilindro, correspondente a .
Ver solução completaQuestão 14
Considere duas placas grandes, paralelas, a uma distância uma da outra, uma delas com densidade superficial de carga , uniforme, e a outra com densidade . Entre as duas placas paralelas é colocada uma chapa metálica de espessura , conforme mostra a figura.
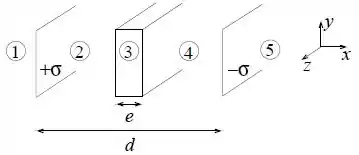
Demonstre que a intensidade do campo elétrico criado por um plano infinito com densidade superficial de carga é .
Utilizando o princípio de superposição e desprezando efeitos de borda, determine o vetor campo elétrico nas regiões e .
Se a chapa metálica for retirada da região entre as placas, haverá aumento ou diminuição da energia eletrostática do sistema? Justifique a resposta.
Ver solução completaQuestão 15
A figura mostra uma seção reta de uma placa não-condutora muito extensa com uma espessura e uma densidade volumétrica de cargas uniforme .
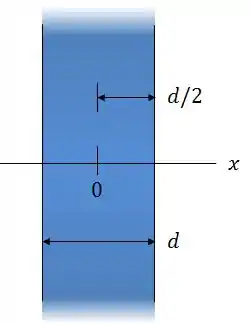
A origem do eixo está no centro da placa.
Determine o módulo do campo elétrico em:
- ;
- ;
- ;
- ;
Questão 16
Uma esfera metálica maciça de raio é concentricamente circundada por uma casca esférica metálica com raios interno e externo , como mostrado na figura abaixo.
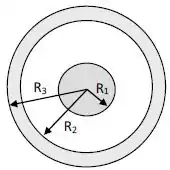
O fluxo elétrico através de uma superfície esférica gaussiana de raio vale . Sabendo que a esfera maciça possui uma carga e considerando que e :
Calcule, utilizando a Lei de Gauss, a distribuição das cargas nas superfícies externa e interna da casca esférica. Qual é o valor da carga líquida da casca? Justifique as afirmações e os cálculos.
Calcule o valor do módulo do campo elétrico na superfície da esfera maciça e na superfície externa da casca.
Considere agora que a casca esférica metálica é substituída por uma casca esférica isolante com e (desenho abaixo). A casca isolante é carregada uniformemente com uma carga igual ao valor da carga líquida da casca metálica anterior.
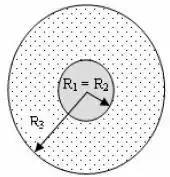
Calcule o valor do fluxo elétrico através de uma superfície gaussiana esférica de raio .
Ver solução completaQuestão 17
Um bastão cilíndrico isolante, de comprimento e raio (com ), foi carregado uniformemente em sua superfície com carga negativa desconhecida (Figura 1). Mediu-se o campo elétrico gerado a uma distância do eixo de simetria e encontrou-se o valor (em módulo).
Calcule o fluxo do campo elétrico através da superfície indicada (sombreada) na Figura 1 (altura e raio ).
Obtenha o vetor campo elétrico em função da distância ao eixo do bastão, para .
Suponha agora que uma casca cilíndrica condutora descarregada (neutra) de comprimento e raios interno e externo é colocada em volta do bastão carregado utilizando-se luva de borracha. Posiciona-se a casca com o eixo de simetria coincidindo com o eixo do bastão (concêntrico), conforme a Figura 2.
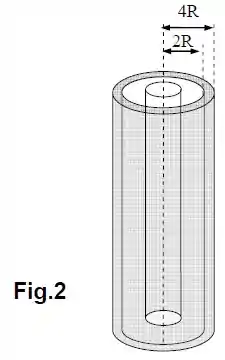
Responda, justificando:
Obtenha o valor (módulo) do campo elétrico à distância do eixo.
Quanto vale a carga na superfície interna e na superfície externa da casca cilíndrica?
Agora suponha que a casca cilíndrica condutora seja aterrada. Responda, justificando:
Quanto vale a carga na superfície interna e na superfície externa da casca cilíndrica?
Calcule o fluxo elétrico que atravessa uma superfície cilíndrica concêntrica ao sistema e de raio .
Ver solução completaQuestão 18
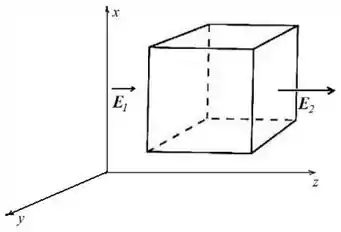
(Capítulo 23.4 – Exercício 11) A Fig. 23-31 mostra uma superfície gaussiana com a forma de um cubo de 2,00 m de aresta, com um vértice no ponto x1 = 5,00 m, y1 = 4,00 m. O cubo está imerso em um campo elétrico dado por, com y em metros. Qual é a carga total contida no cubo?
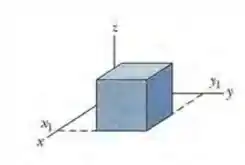
Questão 19
(Capítulo 23.4 – Exercício 8) Quando um chuveiro é aberto em um banheiro fechado, os respingos de água no piso do boxe podem encher o ar de íons negativos e produzir um campo elétrico no ar de até 1000 N/C. Considere um banheiro de dimensões 2,5 m X 3,0 m X 2,0 m. Suponha que no teto, no piso e nas quatro paredes o campo elétrico no ar é perpendicular à superfície e possui um módulo uniforme de 600 N/C. Suponha também que o teto, o piso e as paredes formam uma superfície gaussiana que envolve o ar do banheiro. Determine (a) a densidade volumétrica de cargas ρ e (b) o número de cargas elementares e em excesso por metro cúbico de ar.
Ver solução completaQuestão 20
Considere duas placas finas, planas, infinitas, situadas nos planos cartesianos e , com densidades superficiais de carga iguais a e , respectivamente, onde . Assinale a opção que indica as expressões corretas para o vetor campo elétrico nas regiões
- , ,
- , ,
- ,,
- , ,
- , ,
Questão 21
Um plano infinito, paralelo ao plano , está localizada em e foi carregada com uma densidade de carga superficial (uniforme) de . Um segundo plano infinito, também paralelo ao plano situa-se em e foi carregado com uma densidade superficial de carga de . Qual é o campo elétrico devido a esses dois planos na origem? (onde é o versor unitário na direção .)
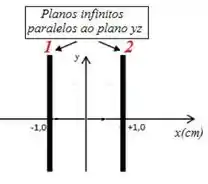
Questão 22
Uma placa isolante, infinita e de espessura está posicionada de forma que seu plano médio coincida com o plano , como mostrado na figura abaixo.
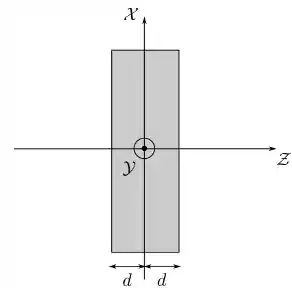
Ela está carregada com uma densidade volumétrica de carga constante e positiva.
Utilizando a lei de Gauss, determine o campo elétrico (módulo, direção e sentido) na região externa à placa, ou seja, .
Utilizando a lei de Gauss, determine o campo elétrico (módulo, direção e sentido) na região interna à placa, ou seja, .
Mostre que o resultado do item é equivalente ao campo produzido por um plano infinito uniformemente carregado com uma densidade superficial de carga . Expresse o valor de em termos dos parâmetros do problema e interprete o resultado.
Ver solução completaQuestão 23
Próximo a um plano (infinito) , com densidade superficial de carga , temos três sistemas, todos com a mesma carga elétrica (não nula):
uma partícula (pontual);
um sólido uniformemente carregado;
uma chapa bidimensional, também uniformemente carregada;
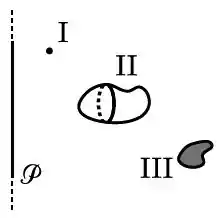
Assinale a opção que melhor indica a relação entre os módulos das forças elétricas devidas ao plano sobre cada um dos sistemas.
.
.
.
.
.
Ver solução completaQuestão 24
Um cilindro circular, muito longo, possui uma densidade volumar de carga elétrica estacionária, mas não uniforme , onde e é a usual coordenada radial, medida a partir do eixo de simetria do cilindro.
Envolvendo tal cilindro, temos uma casca cilíndrica circular espessa, coaxial, também muito longa, de raios interno e externo , condutora e neutra.
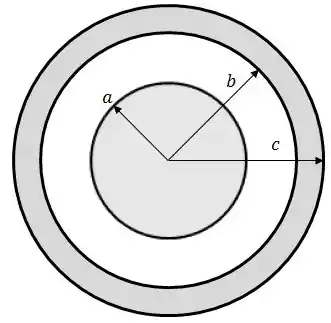
Determine a carga por unidade de comprimento axial, no cilindro interno.
Determine o campo elétrico em um ponto genérico dentro do cilindro interno, com coordenada radial .
Determine o campo elétrico em um ponto genérico na região entre os dois cilindros, com coordenada radial .
Determine o campo elétrico em um ponto genérico dentro da casca condutora, com coordenada radial .
Determine o campo elétrico em um ponto genérico na região exterior aos dois cilindros, com coordenada radial .
Ver solução completaQuestão 25
Seja uma região R delimitada por uma superfície fechada . Tal região possui uma densidade volumar de carga não-uniforme e uma carga total . A partir da lei de Gauss, pode-se dizer que
Se , o campo elétrico é nulo no exterior de .
Além de , é necessário que para que o campo elétrico seja nulo no exterior de .
Se , o fluxo de campo elétrico sobre é nulo.
Além de , é necessário que para que o fluxo de campo elétrico seja nulo em .
Nenhuma das opções anteriores.
Ver solução completaQuestão 26
Um plano dielétrico possui densidade superficial de carga constante (estacionária e uniforme) . Coloca-se, então, a uma distância desse plano, uma placa condutora neutra , de espessura e transversalmente infinita, conforme mostra a figura abaixo.
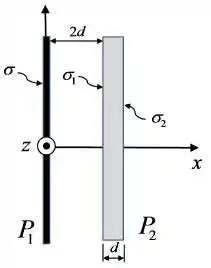
Determine (com justificativas!):
o módulo, a direção e o sentido do campo elétrico produzido apenas pelo plano , para .
o campo no interior da placa condutora.
as densidades de carga induzidas e na placa condutora.
o módulo, a direção e o sentido do campo elétrico na região .
Ver solução completaQuestão 27
A figura abaixo mostra uma esfera não condutora de raio com uma carga uniformemente distribuída. Esta esfera é concêntrica a uma casca esférica condutora de raio interno e raio externo . A casca esférica possui uma carga em excesso de .
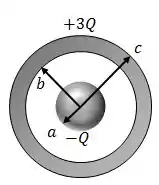
Determine o campo elétrico :
No interior da esfera, ;
Entre a esfera e a casca esférica, ;
Dentro da casca;
Fora da casca, ;
Que cargas surgem sobre as superfícies interna e externa da casca esférica?
Ver solução completaQuestão 28
Considere duas placas grandes, paralelas, a uma distância uma da outra, uma delas com densidade superficial de carga , uniforme, e a outra com densidade . Entre as duas placas paralelas é colocada uma chapa metálica de espessura , conforme mostra a figura.
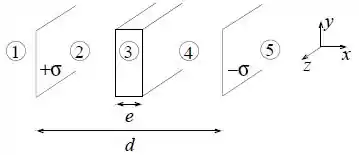
Demonstre que a intensidade do campo elétrico criado por um plano infinito com densidade superficial de carga é .
Utilizando o princípio de superposição e desprezando efeitos de borda, determine o vetor campo elétrico nas regiões e .
Se a chapa metálica for retirada da região entre as placas, haverá aumento ou diminuição da energia eletrostática do sistema? Justifique a resposta.
Ver solução completaQuestão 29
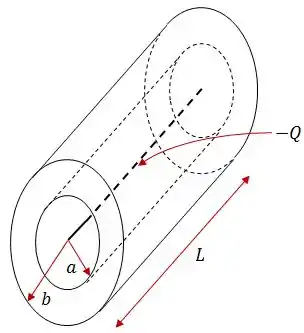
Um cabo coaxial muito longo, de comprimento , é formado por um condutor cilíndrico de raio e por uma casca condutora cilíndrica de raio , conforme ilustrado na figura abaixo. Pelo condutor interno flui uma corrente I no sentido positivo de z positivo e pela casca externa flui uma corrente no sentido de negativo.
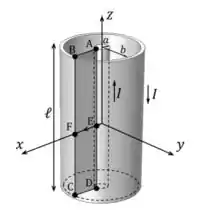
- Calcule o vetor campo magnético na região
- Calcule o fluxo do campo magnético na superfície delimitada pelos pontos ABCD, onde A = (), B = (), C = (), e D = (),
- Calcule ao longo do caminho aberto EF (com a orientação de E para F), onde E = () e F = ().
Questão 30
Uma placa condutora neutra, em equilíbrio eletroestático, quadrada, de lado e espessura , tal que , é colocada a uma distância de um plano de cargas também quadrado de lado , com densidade superficial de cargas dada por (, como mostrado na figura abaixo.
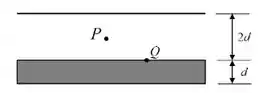
Quais são o módulo do campo elétrico no ponto localizado entre a placa e o plano, e a densidade superficial de cargas , no ponto , sobre a superfície da placa que fica mais próxima do plano?
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 31
Um fio infinito, isolante, com densidade linear de carga uniforme , é colocado sobre uma placa infinita, isolante, com densidade superficial de carga uniforme .
Utiliza-se um sistema de coordenadas cartesianas tal que o fio está ao longo do eixo e a
placa se extende no plano , conforme a figura.
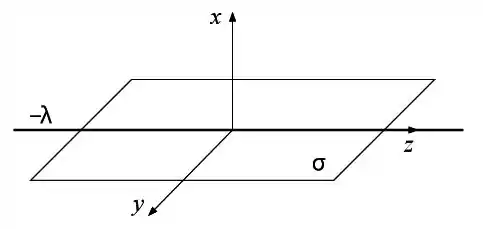
Calcule o vetor campo elétrico produzido pela placa em todo o espaço.
Calcule o vetor campo elétrico produzido pelo fio em todo o espaço.
Determine os pontos do espaço onde a força que atua sobre uma partícula de carga Q é nula.
Ver solução completaQuestão 32
Seja um fio isolante fino (que pode ser considerado reto e infinito) carregado com uma densidade linear de carga uniforme . Este fio está colocado paralelamente e concentricamente com um cilindro condutor (também infinito), de raio interno e raio externo , como mostra a figura 1 abaixo. O cilindro condutor possui, inicialmente, uma densidade linear de carga uniforme .
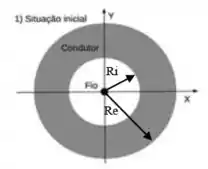
- Calcule as densidades superficiais de carga e , respectivamente, nas superfícies interna e externa do cilindro, considerando que o equilíbrio eletrostático foi atingido.
- Calcule o campo elétrico nas regiões , e .
Agora suponha o cilindro anterior seja substituído por um cilindro isolante, com dimensões idênticas e com exatamente a mesma distribuição de cargas que nos itens a) e b). O mesmo fio usado anteriormente é, então, deslocado ao longo do eixo , de modo que seu centro se encontra agora em , como mostrado na figura 2 abaixo.
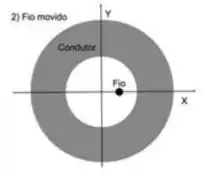
c) Calcule o campo elétrico no ponto .
Ver solução completaQuestão 33
Uma esfera maciça isolante de raio está positivamente carregada. A densidade de carga volumétrica uniforme é dada por . O campo elétrico dentro da esfera vale:
- , apontando radialmente para fora com relação ao centro da esfera.
- , apontando radialmente para dentro com relação ao centro da esfera.
- , apontando radialmente para fora com relação ao centro da esfera.
- , apontando radialmente para dentro com relação ao centro da esfera.
- , apontando radialmente para fora com relação ao centro da esfera
Questão 34
O gráfico da figura mostra a intensidade do campo elétrico como uma função da distância a partir do centro para um par de esferas concêntricas e uniformemente carregadas.

Qual das seguintes situações o gráfico pode representar?
Uma esfera condutora carregada positivamente dentro de uma casca esférica condutora carregada positivamente.
Uma esfera condutora carregada positivamente dentro de uma casca esférica condutora descarregada.
Uma esfera sólida não condutora, carregado uniformemente em todo o seu volume, dentro de uma casca esférica condutora carregada positivamente.
Uma casca esférica de parede fina carregada positivamente dentro de uma casca esférica não condutora carregada positivamente em todo o seu volume.
Uma casca esférica de parede fina carregada positivamente, não condutora, dentro de outra casca esférica não condutora de parede fina carregada positivamente.
Ver solução completaQuestão 35
Sobre a lei de Gauss e sua aplicação, considere as afirmativas abaixo:
A lei de Gauss pode sempre ser usada para o cálculo do fluxo do campo elétrico de qualquer distribuição de cargas;
A lei de Gauss sempre permite a determinação de uma expressão analítica para o campo elétrico produzido por qualquer distribuição de cargas;
Partículas carregadas localizadas em uma região exterior a uma superfície fechada não contribuem para o fluxo de campo elétrico através dessa superfície, mas contribuem para o campo elétrico em pontos sobre a mesma.
São VERDADEIRAS as afirmativas:
e
e
e
I, II e III
Nenhuma delas.
Ver solução completaQuestão 38
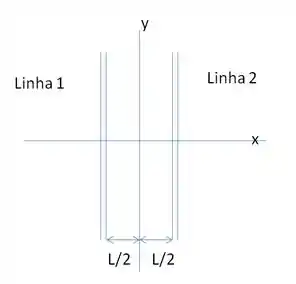
Uma haste fina longa, paralela ao eixo está localizada em e foi carregada com uma densidade de carga uniforme linear . Uma segunda haste fina longa, paralela ao eixo situa-se em foi também carregada com uma densidade de carga uniforme linear .
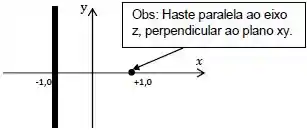
Qual é o campo elétrico devido a essas hastes na origem?
;
;
;
;
zero;
Ver solução completaQuestão 39
O campo elétrico representado na figura está dirigido ao longo do eixo . Ele é uniforme nas direções e , mas sua intensidade varia em função de (em outras palavras ).
Considere uma superfície fechada cilíndrica de raio e comprimento como ilustrado na figura.
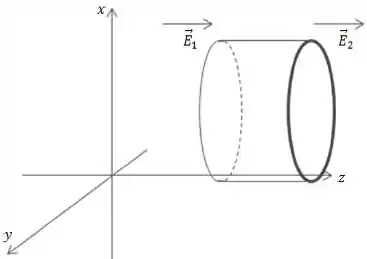
As intensidades do campo elétrico nos lados esquerdo e direito do cilindro são, respectivamente, e . A carga elétrica envolvida pelo cilindro é dada por:
;
;
;
;
;
Ver solução completaQuestão 40
Um fio fino, retilíneo e finito de comprimento está uniformemente carregado com uma carga total . Desenha-se então uma superfície fechada na forma de um cilindro reto de raio e comprimento , como mostrado na figura abaixo. O cilindro é posicionado de forma que seu eixo coincida com o eixo do fio e os centros de suas tampas toquem as extremidades do fio.
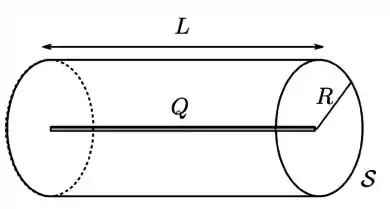
- O campo eletrostático produzido pelo fio é perpendicular a todos os pontos da superfície lateral do cilindro? Justifique.
- O campo eletrostático produzido pelo fio tem a mesma intensidade sobre todos os pontos da superfície lateral do cilindro? Justifique.
- É possível utilizar a lei de Gauss em conjunto com a superfície para se obter uma expressão para o campo eletrostático produzido pelo fio em todo o espaço? Justifique.
Questão 41
Considere um cilindro muito comprido, com raio . O cilindro possui uma densidade volumétrica de carga , onde é uma constante positiva e é a distância medida a partir do eixo do cilindro. Uma fração do cilindro, de comprimento muito maior que e muito menor que o comprimento total do cilindro, é pintado com uma tinta não condutora que possui uma carga total e espessura desprezível.
a) Calcule a carga total (incluindo a carga da tinta) contida num cilindro de comprimento muito maior que e muito menor que o comprimento total do cilindro.
b) Determine o campo elétrico do cilindro de comprimento muito maior que e muito menor que o comprimento total do cilindro, nas regiões: i) ; e ii) .
c) Calcule a força experimentada por uma carga pontual negativa , localizada no exterior do cilindro de comprimento muito maior que e muito menor que o comprimento total do cilindro, i.e., a uma distância .
Ver solução completaQuestão 42
(Capítulo 23.9 – Exercício 45) Duas cascas esféricas concêntricas carregadas têm raios de 10,0 e. A carga da casca menor é e a da casca maior é . Determine o campo elétrico (a) em ; (b) em .
Ver solução completaQuestão 43
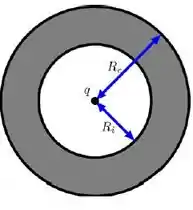
Considere uma carga pontual q posicionada no centro de uma casca esférica isolante de raio interno e raio externo. A casca possui uma carga total distribuída homogeneamente em seu volume.
A Figura serve como guia.
a) Calcule a razão para que o módulo do campo elétrico a uma distância do centro seja nulo (não esqueça o sinal).
Ou seja,
b) Calcule a razão para que o módulo do campo elétrico a uma distância do centro seja nulo (não esqueça o sinal). Ou seja, .
Questão 44
Um cilindro maciço muito longo, não condutor, de raio e comprimento , contém uma densidade volumétrica de carga , uniforme.
Considere a distância ao eixo do cilindro. Desprezando efeitos de borda, determine:
a carga total do cilindro em função de , e ;
o módulo do campo elétrico para ;
o módulo do campo elétrico para .
Esboce o gráfico do módulo do campo elétrico em função de . Indique no gráfico o raio do cilindro.
Ver solução completaQuestão 45
Um cilindro maciço infinito, não condutor, de raio , apresenta uma densidade volumétrica de carga variável dada por , onde é uma constante positiva e é a distância ao eixo de simetria do cilindro.
Considere duas superfícies gaussianas cilíndricas (figura abaixo) e (figura abaixo), com mesmo eixo de simetria do cilindro maciço, alturas , raios e , respectivamente.
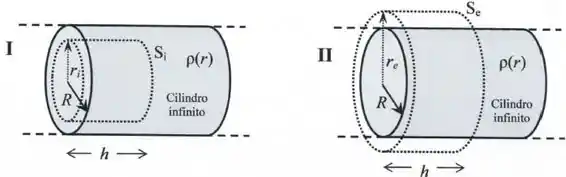
Note que suas respostas podem conter apenas as variáveis , , , , e .
Calcule a carga elétrica no interior de e a carga elétrica contida no interior de .
Calcule o módulo do campo elétrico , para e para .
Esboce um gráfico de em função de , considerando as regiões e .
Ver solução completaQuestão 46
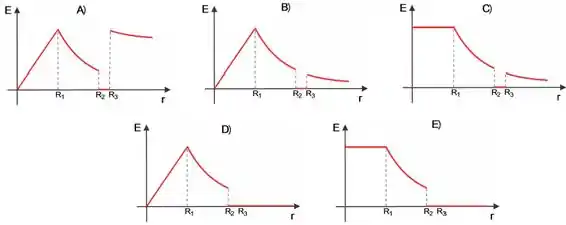
Uma esfera isolante de raio possui uma carga uniformemente distribuída em todo o seu volume. Esta esfera é concêntrica a uma casca esférica condutora de raio interno e raio externo que é carregada com uma carga tal como indicado na figura.
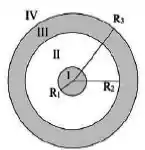
O gráfico que melhor descreve o campo elétrico nas regiões I a IV é:
Questão 47
Para uma casca esférica condutora, de raio interno e raio externo , com centro no ponto e inicialmente neutra, transfere-se uma carga . Em seguida, uma partícula (pontual) de carga é colocada no ponto . Quais são as expressões corretas para as densidades superficiais de carga sobre as superfícies interna e externa da casca condutora, nessa ordem?
- e
- e
- e
- e
- e
- e
- e
Questão 48
Considere uma casca esférica isolante de raio interno e raio externo , conforme a figura. Na região , a casca esférica tem uma densidade volumétrica de carga , onde e é a distância até o centro da casca esférica. Coloca-se no centro da casca esférica uma carga
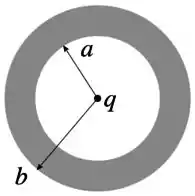
(a) Calcule o vetor campo elétrico na região .
(b) Calcule o vetor campo elétrico fora da casca (região onde ).
(c) Suponha agora que a casca esférica é condutora ao invés de isolante, com carga total . Mantendo a carga no centro da casca, quais seriam os valores das cargas na superfície interna () e na superfície externa ()?
Ver solução completaQuestão 49
Um cilindro circular infinito, isolante, de raio possui uma distribuição volumétrica de carga uniforme.
Que tipo de dependência com a distância ao eixo do cilindro podemos esperar para a intensidade do campo elétrico, , nas regiões do espaço definidas por e , respectivamente?
Ver solução completa
Questão 50
Um disco circular, fino e isolante de raio possui uma densidade superficial de carga constante, como mostra a figura abaixo.
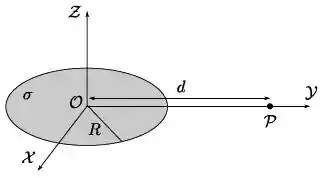
Considere um ponto sobre o eixo , a uma distância do centro do disco. A intensidade do campo elétrico nesse ponto no limite assintótico em que ele está muito afastado do disco, ou seja, quando , é dada por:
Ver solução completa
Questão 51
Considere duas grandes placas planas, paralelas. Uma das placas com uma densidade de cargas se encontra na origem do eixo e a outra, com está localizada em .
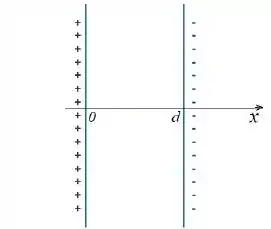
Qual é o vetor campo elétrico no ponto médio se o eixo passa pelo centro das duas placas? (considere que as dimensões das placas são muito maiores que a distância entre elas)
Ver solução completa
Questão 52
Duas cascas esféricas finas e condutoras concêntricas de raios e possuem cargas e , como indicado abaixo.
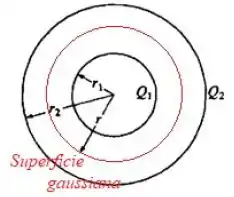
Considere a região onde é à distância até o centro das esferas. Nessa região, o campo elétrico resultante é:
Ver solução completa
Questão 53
A figura ao lado ilustra uma esfera oca condutora de raio interno e raio externo , que tem uma carga elétrica negativa . Uma carga pontual positiva é fixada no centro da esfera oca. Na figura, representa uma distância radial qualquer ao centro da esfera. Existe vácuo nas regiões e .
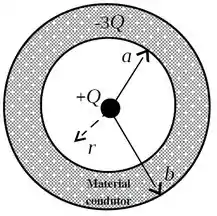
(a) Calcule o vetor campo elétrico (módulo, direção e sentido) em todos os pontos do espaço, ou seja, nas regiões (i) , (ii) e (iii) .
(b) Represente, em um desenho esquemático, um esboço das linhas de campo elétrico nas regiões , e .
(c) Determine a densidade superficial de carga na (i) superfície interna da esfera oca () e na (ii) superfície externa da esfera oca ().
Ver solução completaQuestão 54
Uma esfera isolante com carga uniformemente distribuída é envolta por uma casca esférica, concêntrica, condutora, e de carga , com raio interno e raio externo (). A densidade superficial de carga na parede interna da casca condutora vale:
Questão 55
Considere uma esfera isolante de raio carregada com a densidade volumar de carga , sendo uma constante e a distância de um ponto genérico ao centro da esfera. Considere também uma barra de comprimento e densidade linear de carga constante . A barra está orientada para o centro da esfera e o seu ponto médio está a uma distância do centro da esfera, sendo , como mostrada na figura abaixo.
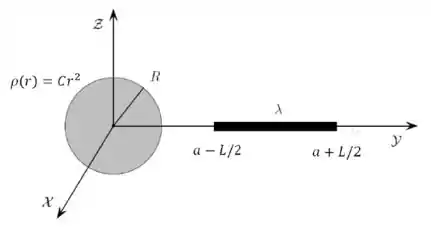
- Determine a carga da esfera.
- Utilizando a lei de Gauss, calcule o campo eletrostático (módulo, direção e sentido) produzido apenas pela esfera, num ponto , situado a uma distância do centro da esfera, tal que .
- Calcule a força eletrostática (módulo, direção e sentido) exercida pela esfera sobre a haste.
- Obtenha uma expressão aproximada para a força exercida pela esfera sobre a haste para e discuta o resultado encontrado.
Questão 56
Uma placa condutora, de lado e espessura desprezível possui uma carga uniformemente distribuída sobre sua superfície. Considere um ponto sobre o eixo perpendicular ao plano da placa e que passa por seu centro, a uma distância do mesmo. Se este ponto está muito próximo da placa, de forma que , a intensidade do campo elétrico produzido pela placa neste ponto vale, aproximadamente:
Questão 57
Um fio fino, retilíneo e finito de comprimento está uniformemente carregado com uma carga total . Desenha-se então uma superfície fechada na forma de um cilindro reto de raio e comprimento , como mostrado na figura abaixo. O cilindro é posicionado de forma que seu eixo coincida com o eixo do fio e os centros de suas tampas toquem as extremidades do fio. Sobre essa situação, considere as afirmativas abaixo:
- O campo elétrico produzido pelo fio tem módulo constante em todos os pontos sobre a superfície lateral do cilindro.
- O campo elétrico produzido pelo fio é tangente a todos os pontos das tampas do cilindro.
- O fluxo de campo elétrico produzido pelo fio através de vale .
São VERDADEIRAS as afirmativas:
- I
- II
- III
- I e II
- I e III
- II e III
- I, II e III
- Nenhuma delas.
Questão 58
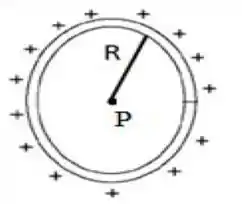
O anel da figura abaixo tem raio e uma carga positiva uniformemente distribuída sobre ele. Qual é o campo elétrico no ponto localizado no centro do anel?
Questão 59
A figura abaixo ilustra uma esfera maciça e não-condutora, de raio e densidade volumétrica de carga constante e positiva . Na figura, denota uma distância radial arbitrária ao centro da esfera. Tal esfera está localizada no vácuo, cuja constante de permissividade elétrica é dada por .
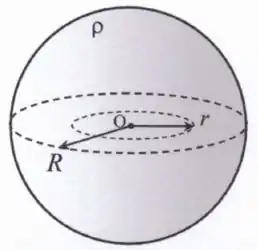
- Calcule o módulo do campo elétrico na região .
- Calcule o módulo do campo elétrico na região .
- Esboce um gráfico qualitativo descrevendo como os módulos dos campos elétricos calculados nos itens (a) e (b) acima variam com a distância , onde .
Questão 60
Considere uma casca esférica (não condutora) que está centrada na origem . Ela é uniformemente carregada com carga e possui raio , cujo centro situa-se à uma distância de um plano infinito, uniformemente carregado com uma densidade superficial , conforme mostrado na figura abaixo.
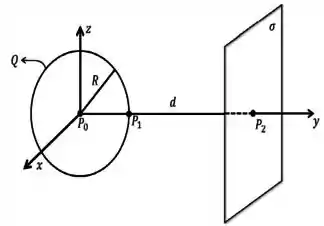
- Determine o vetor campo elétrico em todo o espaço devido à casca esférica.
- Determine o vetor campo elétrico em todo o espaço devido à carga na superfície plana.
- Determine o vetor campo elétrico resultante ao longo do eixo .
- Calcule a diferença de potencial entre os pontos e localizados na superfície plana e no centro da casca, respectivamente.
Questão 61
Suponha que exista uma superfície gaussiana fechada, que possui somente duas cargas em seu interior e , ambas com o mesmo sinal. Sabendo que podemos afirmar que o valor do fluxo do campo elétrico é igual a:
uponha que exista uma superfície gaussiana fechada, que possui somente duas cargas em seu interior (Q1
e Q2), ambas com o mesmo sinal. Sabendo que |Q1|=|Q2|=Q podemos afirmar que o valor do fluxo do
campo elétrico é igual a:
uponha que exista uma superfície gaussiana fechada, que possui somente duas cargas em seu interior (Q1
e Q2), ambas com o mesmo sinal. Sabendo que |Q1|=|Q2|=Q podemos afirmar que o valor do fluxo do
campo elétrico é igual a:
Ver solução completaQuestão 62
(Capítulo 23.8 – Exercício 40) A Fig. 23-46 mostra uma placa não condutora muito extensa que possui uma densidade superficial de cargas uniforme ; a figura mostra também uma partícula de carga , a uma distância da placa. Ambas estão fixas no lugar. Se , para que coordenada (a) positiva e (b) negativa sobre o eixo (além do infinito) o campo elétrico total , é zero? (c) Se , para que coordenada sobre o eixo x o campo
é zero?
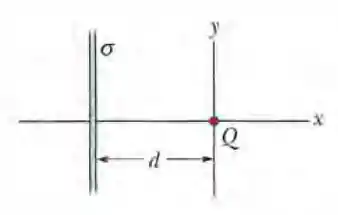
Questão 63
Considere um capacitor formado por duas cascas cilíndricas metálicas de raios (interno) e raio (externo) com cargas e , respectivamente. Ambos os cilindros são muito longos e possuem comprimento , de forma que efeitos de borda podem ser desprezados.
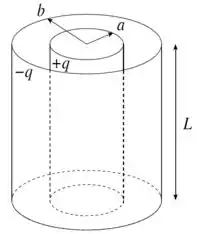
- Calcule a densidade de carga nas superfícies interna e externa do capacitor. Expresse suas respostas em termos de e das dimensões do sistema.
- Determine o vetor campo elétrico em todo o espaço.
- Determine a capacitância do capacitor.
Questão 64
Uma carga puntiforme positiva e um fio infinito carregado positivamente com densidade de carga estão ilustrados na figura abaixo. A direção do fio é perpendicular à folha de papel. Considere os campos elétricos gerados pelos dois objetos em função da distância de cada um deles. Para qual distância os campos elétricos gerados são idênticos:
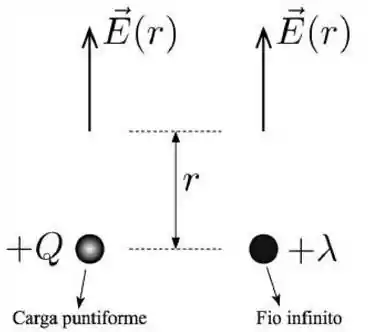
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 65
Duas placas grandes, planas e orientadas horizontalmente são paralelas entre si, a uma distância uma da outra. A meio caminho entre as duas placas, o campo elétrico resultante tem magnitude . Se a separação das placas é reduzida para , qual é a magnitude do campo elétrico a meio caminho entre as placas?
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 66
A figura abaixo mostra uma esfera isolante, maciça, uniformemente carregada, de raio , com densidade volumétrica de carga ().
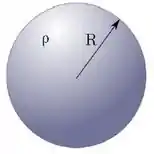
Determine o módulo do vetor campo elétrico nas regiões e , onde é a distância radial medida desde o centro da esfera.
Ver solução completaQuestão 67
Uma esfera condutora maciça de raio encontra-se carregada com uma carga total . Ela está envolvida por uma casca esférica isolante de raio interno e raio externo (), uniformemente carregada com uma densidade volumétrica de carga , como mostrado na figura abaixo. A esfera e a casca são concêntricas e o sistema se encontra em equilíbrio eletrostático.
Utilizando a lei de Gauss, determine o vetor campo elétrico produzido pelo sistema em um ponto a uma distância r do centro da esfera. Considere todas as regiões distintas do espaço, dadas por
(i); (ii) ; (iii) ; e (iv) .
Justifique cuidadosamente todos os argumentos utilizados.
Ver solução completaQuestão 68
Dois planos infinitos e paralelos encontram-se uniformemente carregados com densidades superficiais de carga e , como mostrado na figura abaixo. Sejam , e os módulos do campo elétrico resultante produzido pelos dois planos nos pontos 1, 2 e 3 indicados na figura, respectivamente. Nessa situação, podemos afirmar que:
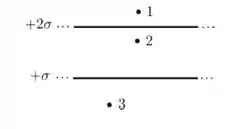
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 69
Uma seção de comprimento do cilindro infinito de raio , mostrado na Figura 1, tem carga total . Esta carga se distribui no volume definido pela seção de acordo com densidade volumétrica de carga . A densidade não varia ao longo do eixo do cilindro, o que permite definir a densidade linear de carga . Determine a relação entre e , considerando os valores de e conhecidos.
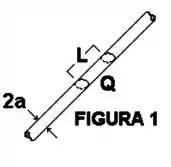
Determine o módulo do vetor campo elétrico em um ponto qualquer afastado da distância (onde do eixo do cilindro infinito (Figura 1), considerando o valor de conhecido.
Três cilindros idênticos (raio e densidade linear de carga ) estão alinhados com os eixos coordenados, conforme mostra a Figura 2. Determine o vetor campo elétrico em um ponto de coordenadas situado no plano e fora dos três cilindros, desprezando as distorções devidas à junção situada em torno da origem.
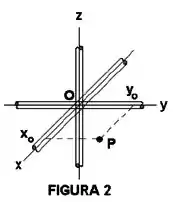
Questão 70
Uma esfera isolante de raio possui densidade volumétrica de carga não uniforme dada pela função , onde a constante vale . O sistema de coordenadas está indicado na figura (o eixo sai do plano da figura). Use .
Adote uma superfície gaussiana esférica centrada na origem e de raio . Use-a para calcular o módulo do campo elétrico produzido em todos os pontos a da origem.
Calcule, utilizando o resultado do item anterior, o vetor campo elétrico no ponto de coordenadas ().
Suponha agora que uma caixa cúbica condutora de paredes espessas, carregada com carga líquida , seja colocada de forma a envolver totalmente nossa esfera isolante e eventualmente outras cargas. Suponha que a carga total da esfera isolante seja . Medindo-se toda a quantidade de carga presente na superfície externa da caixa metálica encontrou-se .
Existem outras cargas, além da esfera isolante, na caixa metálica? Justifique sua afirmação e, em caso de resposta afirmativa, calcule o valor total destas outras cargas.
Ver solução completaQuestão 71
Uma partícula com carga foi depositada bem no centro da cavidade de uma casca esférica condutora de raio interno e raio externo . O gráfico ao lado da figura mostra o fluxo através de uma esfera gaussiana com centro na partícula em função do raio da esfera.
(Considere ou .)
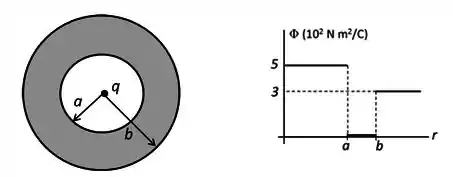
Determine a carga da partícula central e a carga líquida presente na casca condutora.
Considere agora que e . Encontre a dependência do campo elétrico como função de , para as três regiões: , e . Depois , copie na folha de respostas o par de eixos a seguir e esboce nele a função encontrada, calculando os valores importantes e explicitando no gráfico.
Remove-se a partícula e a cavidade é preenchida com um material isolante. A carga no isolante apresenta simetria esférica e densidade volumétrica dada pela função , onde é uma constante. Esta distribuição de carga provoca um campo elétrico radial e de módulo constante e igual a dentro da cavidade. Calcule o valor da constante com sua respectiva unidade SI.
Ver solução completaQuestão 72
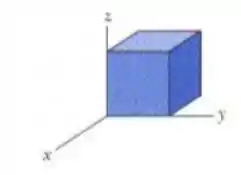
(Capítulo 23.4 – Exercício 10) A Fig. 23-30 mostra uma superfície gaussiana com a forma de um cubo de de aresta, imersa em um campo elétrico dado por, com em metros. Qual é a carga total contida no cubo?
Questão 73
(Capítulo 23.4 – Exercício 7) Uma carga pontual de está no centro de uma superfície Gaussiana cúbica de 55 cm de aresta. Qual é o fluxo elétrico através da superfície?
Ver solução completaQuestão 74
(Capítulo 23.9 – Exercício 55) Uma distribuição de cargas não uniforme, mas com simetria esférica, produz um campo elétrico de módulo , onde é uma constante e r é a distância do centro da esfera. O campo aponta para longe do centro da esfera. Qual é a distribuição volumétrica de cargas ?
Ver solução completaQuestão 75
(Capítulo 23.9 – Exercício 53) Uma esfera não condutora de raio possui uma distribuição de cargas não uniforme , onde é a distância do centro da esfera. (a) Determine a carga da esfera. Determine o módulo do campo elétrico (b) em ; (c) em ; (d) em (e) Faça um gráfico de E em função de .
Ver solução completaQuestão 76
(Capítulo 23 – Problemas Adicionais – Exercício 70) Uma esfera não condutora com 5,0 cm de raio possui uma densidade volumétrica uniforme de cargas . Determine o módulo do campo elétrico (a) a 3,5 cm e (b) a 8,0 cm do centro da esfera.
Ver solução completaQuestão 77
(Capítulo 23.7 – Exercício 30) Na Fig. 23-39, pequenas partes de duas linhas paralelas de cargas muito compridas são mostradas, fixas no lugar, separadas por uma distância . A densidade uniforme de cargas das linhas é para a linha e para a linha . Em que ponto do eixo o campo elétrico é zero?
Questão 78
(Capítulo 23.7 – Exercício 27) Um fio reto longo possui cargas negativas fixas com uma densidade linear de . O fio é envolvido por uma casca coaxial cilíndrica, não condutora, de paredes finas, com de raio . A casca possui uma carga positiva na superfície externa, com uma densidade superficial , que anula o campo elétrico do lado de fora da casca. Determine o valor de .
Ver solução completaQuestão 79
(Capítulo 23 – Problemas Adicionais – Exercício 73) Uma esfera não condutora tem uma densidade volumétrica de cargas uniforme . Seja r o vetor que liga o centro da esfera a um ponto genérico P no interior da esfera. (a) Mostre que o campo elétrico no ponto P é dado por . (Observe que o resultado não depende do raio da esfera.) (b) Uma cavidade esférica é aberta na esfera, como mostra a Fig. 23-56. Usando o princípio da superposição, mostre que o campo elétrico no interior da cavidade é uniforme e é dado por , onde é o vetor que liga o centro da esfera ao centro da cavidade.
Ver solução completaQuestão 80
(Capítulo 23.7 – Exercício 24) A Fig. 23-36 mostra uma seção de um tubo longo de metal, de paredes finas, com um raio e uma carga por unidade de comprimento . Determine o módulo do campo elétrico a uma distância radial (a) ; (b) . (c) Faça um gráfico de em função de para .
Ver solução completaQuestão 81
(Capítulo 23.9 – Exercício 52) A Fig. 23-53 mostra uma casca esférica com uma densidade volumétrica de cargas uniforme , raio interno e raio externo . Determine o módulo do campo elétrico (a) em ; (b) em ; (c) em ; (d) em ; (e) em ; (f) em .
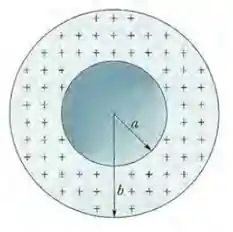
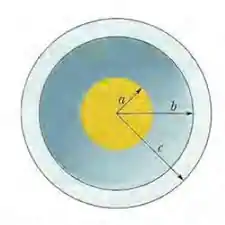
Questão 82
(Capítulo 23.9 – Exercício 49) Na Fig. 23-50, uma esfera maciça de raio é concêntrica com uma casca esférica condutora de raio interno e raio externo . A esfera possui uma carga uniforme e a casca possui uma carga . Determine o módulo do campo elétrico
em ;
em ;
em ;
em ;
em ;
em .
Determine a carga
na superfície interna e
na superfície externa da casca.
Questão 83
. Um cabo coaxial simples consiste de um cilindro condutor maciço, infinito, de seção transversal circular de raio e uma casca condutora cilíndrica, infinita e coaxial ao cilindro, de raio interno e raio externo . O cilindro possui uma quantidade de carga por unidade de comprimento ao longo do eixo igual a e a casca possui uma quantidade de carga por unidade de comprimento igual a , onde é uma constante positiva. Nessa situação, podemos afirmar que a densidade superficial de carga na superfície interna da casca e o módulo do campo elétrico a uma distância do eixo comum, tal que , valem, respectivamente:
Escolha uma opção:
e
e
e
e
e
e
e
e
Ver solução completaQuestão 84
Duas placas condutoras infinitas, neutras, possuem espessura e encontram-se a uma mesma distância de um plano infinito, de espessura desprezível, carregado com uma densidade superficial de carga , como mostrado na figura abaixo. As três placas encontram-se em equilíbrio eletrostático. Nessa situação, as densidades superficiais de cargas nos pontos e indicados na figura, localizados sobre as superfícies das placas mais próximas do plano, valem, respectivamente:
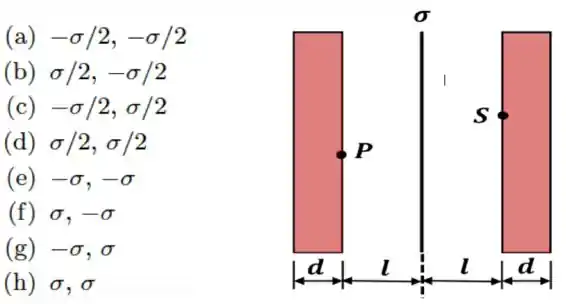
Questão 85
A figura mostra uma esfera metálica e maciça posicionada no centro de uma outra esfera metálica oca. (Na figura, , e )
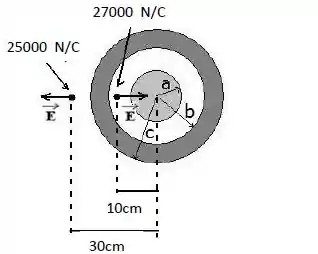
.
Qual é a carga total distribuída na superfície externa da esfera oca?
;
;
;
;
;
Ver solução completaQuestão 86
Considere o objeto abaixo (um paralelepípedo) com uma carga colocada em seu centro geométrico .
- Qual o fluxo total do campo elétrico através da superfície do objeto?
- Você pode calcular o campo elétrico em qualquer ponto da superfície do objeto sem usar a lei de Coulomb? Como?
- Qual é o fluxo total do campo elétrico através do cubo? Você pode calcular o fluxo em cada uma das faces? Qual o fluxo em cada face?
- Você pode calcula o campo elétrico em qualquer ponto da superfície do cubo sem usar a lei de Coulomb? Como?
- Qual é o módulo do campo elétrico em cada um dos vértices do cubo?
Troque o objeto por um cubo de lado . A carga é deslocada para o centro do cubo .
Questão 87
Uma esfera sólida isolante de raio possui uma densidade de carga uniforme em todo seu volume.
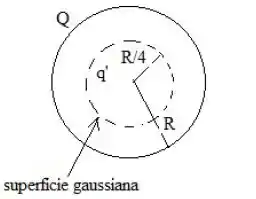
O módulo do campo elétrico a uma distância do centro desta esfera vale:
Ver solução completa
Questão 88
Considere as afirmações abaixo:
- Um sistema com simetria planar é invariante por translações ao longo de um eixo cartesiano apenas.
- A simetria esférica é caracterizada pela invariância por rotações em torno de quaisquer eixos cartesianos.
- Um fio reto e infinito, uniformemente carregado com carga negativa possui simetria cilíndrica.
- Um fio reto de comprimento , uniformemente carregado com carga positiva possui simetria cilíndrica.
- Uma carga pontual possui simetria esférica.
Marque a opção que possui todas as opções verdadeiras.
- I, II e III.
- II, III e V.
- III e V.
- II, III e IV.
- I, III e V.
Questão 89
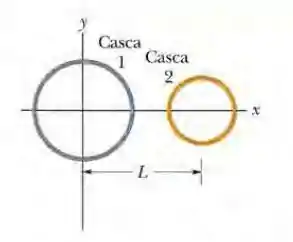
(Capítulo 23.4 – Exercício 12) A Fig. 23-32 mostra duas cascas esféricas não condutoras mantidas fixas no lugar. A casca 1 possui uma densidade superficial de cargas uniforme de +6,0 μC/m2 na superfície externa e um raio de 3,0 cm; a casca 2 possui uma densidade superficial de cargas uniforme de +4,0 μC/m 2 na superfície externa e um raio de 2,0 cm; os centros das cascas estão separados por uma distância L = 10 cm. Em termos dos vetores unitários, qual é o campo elétrico no ponto x = 2,0 cm?
Questão 90
(Capítulo 23.4 – Exercício 13) Observa-se experimentalmente que o campo elétrico em uma certa região da atmosfera terrestre aponta verticalmente para baixo. A uma altitude de 300 m, o campo tem um módulo de 60,0 N/C; a uma altitude de 200 m, o módulo é 100 N/C. Determine a carga em excesso contida em um cubo com 100 m de aresta e faces horizontais a 200 e 300 m de altitude.
Ver solução completaQuestão 91
Uma casca esférica condutora, de raio interno e raio externo , encontra-se carregada com uma carga total . Uma partícula de carga é posicionada no centro da casca. Sabendo que o sistema encontra-se em equilíbrio eletrostático e sendo a distância medida a partir do centro da casca, a intensidade do campo eletrostático produzido pelo sistema nas regiões do espaço definidas por e vale, respectivamente:
- e
- e
- e
- e
- e
- e
- e
Questão 93
O valor do módulo do campo elétrico presente na superfície de uma esfera condutora de raio , mostrada na figura abaixo, é igual a . O campo elétrico aponta para o interior da esfera.
Calcule a carga resultante na superfície da esfera (deixe o resultado em função de e ).
Considere agora que um anel isolante uniformemente carregado com carga total igual a é colocado numa distância do centro da esfera como indicado na figura acima (o anel é visto de perfil).
Sabendo que o raio do anel é , calcule o vetor campo elétrico resultante no ponto de coordenada (deixe o resultado em função de ).
Ver solução completaQuestão 94
(Capítulo 23.4 – Exercício 6) Em todos os pontos da superfície do cubo da Fig. 23-27, o campo elétrico é paralelo ao eixo z. O cubo tem 3,0 m de aresta. Na face superior do cubo, ; na face inferior,. Determine a carga que existe no interior do cubo.
Ver solução completaQuestão 95
(Capítulo 23.4 – Exercício 4) Na Fig. 23-28, uma rede para pegar borboletas está imersa em um campo elétrico uniforme de módulo . O plano do aro da rede, uma circunferência de raio , é mantido perpendicular à direção do campo. A rede é eletricamente neutra. Determine o fluxo elétrico através da rede.
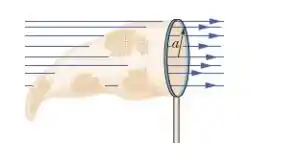
Questão 96
(Capítulo 23.7 – Exercício 32) Um cilindro maciço, longo, não condutor, com de raio, possui uma densidade volumétrica de cargas não uniforme que é função da distância radial a partir do eixo do cilindro: . Se , determine o módulo do campo elétrico (a) para ; (b) para
Ver solução completaQuestão 97
Um cubo isolante de aresta encontra-se uniformemente carregado em todo o seu volume e possui uma carga total . Desenha-se, então, uma superfície fechada , também cúbica e de aresta , concêntrica ao cubo original e com faces paralelas ao mesmo, como mostra a figura abaixo.
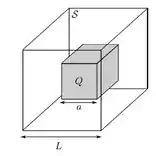
Sobre esse sistema, considere as afirmativas abaixo:
- O fluxo do campo elétrico produzido pelo cubo através de tem módulo igual a .
- O campo elétrico produzido pelo cubo tem a mesma direção em todos os pontos de uma das faces de .
- O campo elétrico produzido pelo cubo tem o mesmo módulo em todos os pontos de .
São corretas as afirmativas:
- Somente e
- Somente
- Somente
- Somente e
- Somente e
- Somente
- , e
- Nenhuma delas.
Questão 98
Considere um disco circular isolante fino, de raio , carregado com uma carga total uniformemente distribuída sobre sua superfície. Desenha-se, então, uma superfície imaginária , fechada, na forma de um cilindro circular reto de raio , comprimento e eixo coincidente com o eixo do disco. Suas tampas são paralelas ao disco e equidistantes dele. Sobre essa situação, considere as afirmativas abaixo:
- O fluxo de campo elétrico produzido pelo disco através de é igual a .
- O campo elétrico produzido pelo disco tem a mesma intensidade em todos os pontos sobre a superfície lateral do cilindro.
- O campo elétrico produzido pelo disco tem a mesma intensidade em todos os pontos sobre as tampas do cilindro.
São VERDADEIRAS as afirmativas:
- e
- e
- e
- , e
- Nenhuma delas.
Questão 99
Um cubo isolante de aresta encontra-se uniformemente carregado em todo o seu volume e possui uma carga total . Desenha-se, então, uma superfície fechada , também cúbica e de aresta (), concêntrica ao cubo original e com faces paralelas ao mesmo, como mostra a figura abaixo.
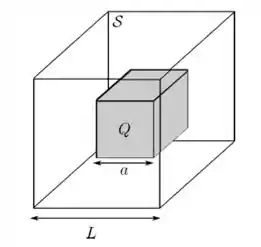
- O campo elétrico produzido pelo cubo tem a mesma intensidade em todos os pontos da superfície ? Justifique.
- O campo elétrico produzido pelo cubo é perpendicular à superfície em todos os seus pontos?
- Podemos usar a lei de Gauss em conjunto com a superfície para obter explicitamente uma expressão para o campo elétrico produzido pelo cubo na região fora dele? Justifique.
Questão 100
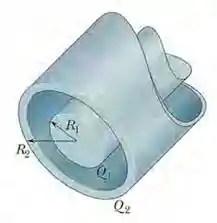
(Capítulo 23.7 – Exercício 31) A Fig. 23-38 é uma seção de uma barra condutora de raio e comprimento no interior de uma casca coaxial, de paredes finas, de raio e mesmo comprimento . A carga da barra é ; a carga da casca é . Determine (a) o módulo e (b) a direção (para dentro ou para fora) do campo elétrico a uma distância radial . Determine (c) e (d) a direção do campo elétrico para . Determine a carga (e) na superfície interna e (f) na superfície externa da casca.
Questão 101
(Capítulo 23.9 – Exercício 51) Na Fig. 23-52, uma casca esférica não condutora com um raio interno e um raio externo possui uma densidade volumétrica uniforme de cargas positivas , onde é uma constante e ré a distância em relação ao centro da casca. Além disso, uma pequena esfera de carga está situada no centro da casca. Qual deve ser o valor de para que o campo elétrico no interior da casca () seja uniforme?
Questão 102
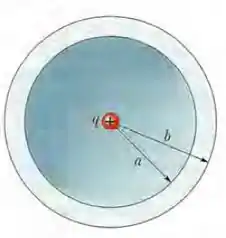
Uma casca esférica de raio tem uma carga total , uniformemente distribuída em sua superfície. Uma segunda casca esférica de raio , concêntrica com a primeira tem carga , também uniformemente distribuída em sua superfície.
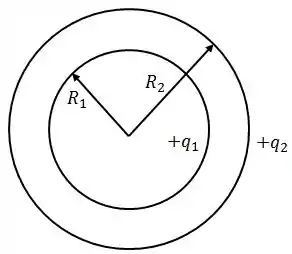
Utilize a Lei de Gauss para determinar o vetor campo elétrico nas regiões onde: , e ;
Qual seria a relação entre as cargas e seus sinais relativos para que o campo elétrico fosse nulo para ?
Esquematize as linhas de forças de campo elétrico para a situação quando a carga é positiva;
Ver solução completaQuestão 103
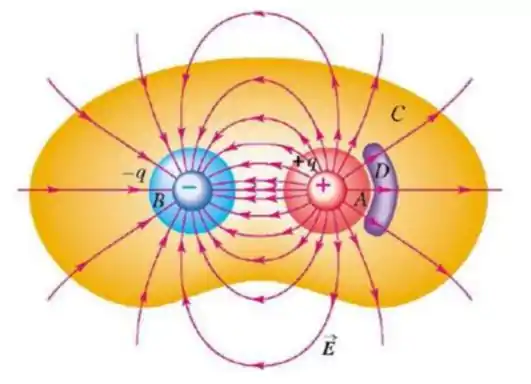
A figura mostra o campo elétrico gerado por um dipolo elétrico. Determine o fluxo elétrico através da superfície
Questão 104
Um cilindro circular muito longo de raio , isolante, com densidade volumétrica uniforme de cargas iguais a , é concêntrico a uma camada cilíndrica condutora de raio interno e raio externo com carga total zero.
O campo elétrico no ponto imediatamente fora do condutor vale .
Nos itens abaixo despreze o campo elétrico e as cargas nas extremidades do cilindro e da camada cilíndrica.
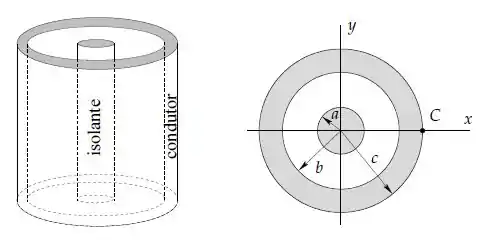
- Calcule o campo elétrico para e .
- Calcule o campo elétrico para .
- Calcule as densidades superficiais de carga e nas superfícies externa e interna da camada cilíndrica condutora em função de , , e .
Questão 105
Uma camada esférica condutora neutra tem raio interno e raio externo . No centro da camada, na cavidade interna, há uma carga puntiforme .
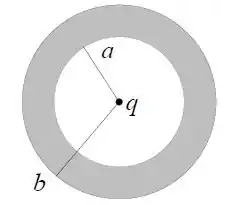
- Usando a lei de Gauss e propriedades dos condutores em equilíbrio eletrostático determine as densidades superficiais de carga e nas superfícies interna e externa da camada esférica.
- Calcule o vetor campo elétrico em todo o espaço.
Questão 106
A figura mostra a visão de perfil de três placas não condutoras de grande extensão densidades superficiais uniforme de cargas com valores , e (). Usando o princípio da superposição, determine
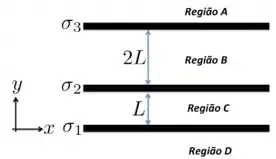
- O vetor campo elétrico nas regiões A, B, C e D;
- A diferença de potencial entre as placas com densidades e ;
- O trabalho do campo elétrico quando um elétron é deslocado entre as placas com densidade e .
Questão 107
Uma casca cilíndrica circular muito longa (infinita), de raio interno e raio externo , está uniformemente carregada, com uma densidade volumar constante.
- Determine a sua carga por unidade de comprimento (axial);
- Determine o vetor campo elétrico para um ponto arbitrário na região ;
- Determine o vetor campo elétrico para um ponto arbitrário na região ;
- Determine o vetor campo elétrico para um ponto arbitrário na região .
Questão 108
Suponha um cilindro dielétrico oco de raio com densidade superficial de carga , envolto por outro cilindro oco de raio com densidade superficial de carga . Os eixos os cilindros são coincidentes. Os valores do módulo do campo elétrico para e a razão para que o campo elétrico seja nulo em qualquer valor de são respectivamente:
Ver solução completaQuestão 109
Uma carga puntiforme está no centro de uma camada esférica condutora de raio interno e raio externo , carregada com uma carga .
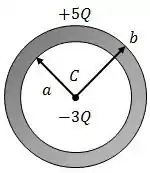
Utilizando a Lei de Gauss, determine o campo elétrico , para e , onde é a distância ao centro da camada;
Obtenha as cargas nas superfícies interna e externa da camada esférica e suas respectivas densidades de cargas nelas;
Ver solução completaQuestão 110
Uma distribuição de cargas, esfericamente simétrica, tem densidade volumétrica
onde é uma constante positiva.
Calcule a carga contida em uma esfera de raio concêntrica com a distribuição de carga. Calcule a carga total da distribuição.
Calcule o vetor campo elétrico para .
Calcule o vetor campo elétrico para .
Ver solução completaQuestão 111
Uma partícula de carga é colocada no centro de um condutor em formato de casca esférica, de raios interno e externo , carregado com carga total . A situação é mostrada na figura abaixo.
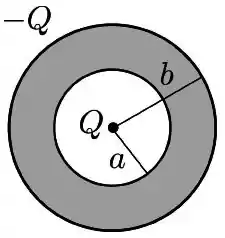
Sabe-se ainda que o sistema está em equilíbrio eletrostático.
Utilizando a lei de Gauss, determine o campo elétrico (módulo, direção e sentido) nas regiões do espaço definidas por , e , onde é a distância ao centro da casca. Esboce o gráfico de sua intensidade como função de .
Determine a densidade superficial de carga nas superfícies interna e externa da casca condutora.
Num ponto distando do centro do condutor é colocada e fixada uma partícula de carga Q. Após reestabelecido o equilíbrio eletrostático no condutor, a força elétrica sobre essa nova carga será atrativa, repulsiva ou nula? Justifique sua resposta.
Ver solução completaQuestão 112
Considere uma superfície fechada S tal que o fluxo de campo elétrico através dela é nulo. Sobre essa situação, considere as afirmativas abaixo:
(I) O campo elétrico é necessariamente nulo em todos os pontos da superfície S.
(II) O campo elétrico é necessariamente nulo em todos os pontos no interior de S.
(III) Não pode haver nenhuma partícula carregada no interior de S.
São VERDADEIRAS as afirmativas:
(a) Nenhuma delas
(b) Apenas I
(c) Apenas II
(d) Apenas III
(e) Apenas I e II
(f) Apenas I e III
(g) Apenas II e III
(h) I, II e III
Ver solução completaQuestão 113
Uma casca esférica condutora de raio interno e raio externo é carregada com carga , conforme a figura abaixo.
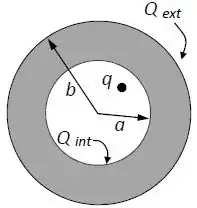
No interior do condutor há uma carga pontual . Denominamos por e , as cargas nas superfícies interna e externa do condutor, respectivamente, quando este chega ao equilíbrio.
Considere as afirmativas abaixo:
Se e , então, para , o campo elétrico aponta radialmente para fora e seu módulo é:
Se e , então, para , o campo elétrico aponta radialmente para dentro e seu módulo é:
Se e , então e .
Se e , então e .
Se as cargas e forem ambas positivas o campo elétrico dentro docondutor não será nulo.
São verdadeiras as afirmativas:
e;
e;
e;
e;
e;
e.
Ver solução completaQuestão 114
Uma carga positiva é distribuída uniformemente pelo volume de cada uma de duas esferas isolantes de raio . Como mostra a figura, uma das esferas está centrada na origem e a outra está centrada em .
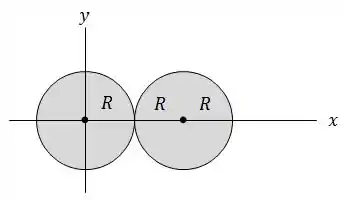
Encontre o vetor campo elétrico resultante devido a essas esferas nos seguintes pontos:
de coordenadas ;
de coordenadas ;
de coordenadas ;
Ver solução completaQuestão 115
Qual das seguintes afirmações sobre a lei de Gauss está correta?
A lei de Gauss é válida somente para distribuição de cargas simétricas, como esferas e cilindros.
Se não houver nenhuma carga no interior de uma superfície de Gauss, o campo elétrico deve ser zero na superfície Gaussiana.
Só a carga total dentro de uma superfície Gaussiana pode produzir um campo elétrico nos pontos dessa superfície.
Se uma superfície Gaussiana está completamente dentro de um condutor, a carga total dentro da Gaussiana nem sempre é zero.
O fluxo elétrico total que passa através de uma superfície de Gauss depende apenas da quantidade de carga total dentro dessa superfície, não do seu tamanho ou forma.
Ver solução completaQuestão 116
Medidas na superfície de nosso planeta, cujo raio médio é , sugerem que o campo elétrico aí é orientado para baixo e que o valor médio de sua componente normal é . Aceitas tais informações e considerando que , qual valor abaixo melhor aproxima a carga total de nosso planeta?
(a) .
(b) .
(c) .
(d)
(e) , pois a Terra é neutra, senão levaríamos choques elétricos o tempo todo.
(f)
(g)
Ver solução completaQuestão 117
A figura 2 ilustra uma casca esférica não-condutora de raio interno e raio externo que possui uma densidade volumétrica de carga positiva constante . Uma carga elétrica pontual positiva está situada no centro da casca.
Na figura 2, representa a distância ao centro da casca esférica.
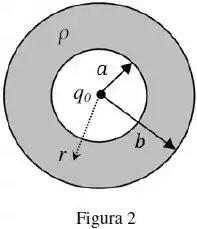
Para este arranjo eletrostático, calcule:
A carga total do sistema.
O vetor campo elétrico em todas as regiões do espaço: ; ; .
Ver solução completaQuestão 118
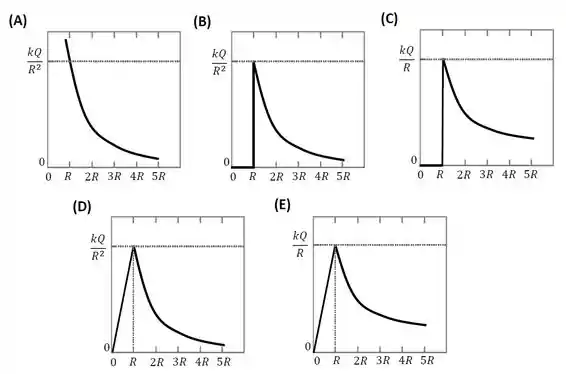
Uma esfera maciça de raio , feita de material condutor, está carregada com uma carga . Se representa o módulo do campo elétrico gerado pela esfera carregada, onde é a distância ao centro da esfera, o gráfico que reproduz a função CORRETAMENTE é:
Questão 119
Uma casca esférica condutora de raio interno e raio externo está carregada com carga elétrica positiva . No centro da casca, na cavidade interna, há uma carga puntiforme .
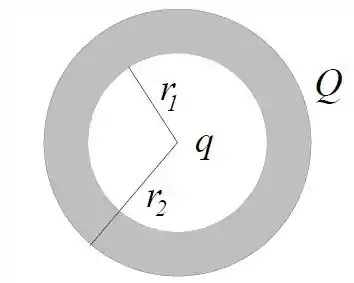
Determine a densidade superficial de carga na superfície interna do condutor.
Calcule o campo elétrico na região externa do condutor.
Ver solução completaQuestão 120
Uma placa isolante, com espessura e densidade volumétrica de carga uniforme igual a , está separada de uma outra placa, condutora, com carga total igual a zero e de espessura . As duas placas são infinitas nas direções e , conforme a figura.
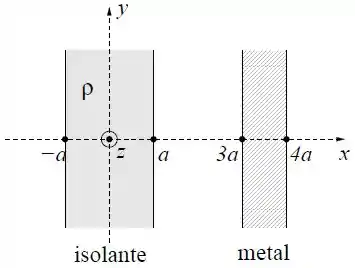
Use a lei de Gauss para calcular o vetor campo elétrico produzido pela placa isolante em um ponto dentro da placa, isto é um ponto com coordenada .
Use a lei de Gauss para calcular o vetor campo elétrico produzido pela placa isolante em um ponto fora dela.
Calcule, em termos de e , a densidade superficial de cargas induzidas nas superfícies da placa condutora após o equilíbrio eletrostático ter sido atingido. Determine em todo o espaço o campo elétrico resultante devido ao isolante e ao condutor.
Ver solução completaQuestão 121
Q - Uma distribuição esférica de carga de raio possui densidade dada por em que é uma constante positiva dada por .
Calcule o campo elétrico produzido em um ponto arbitrário dentro e em um ponto arbitrário fora da distribuição. Deixe o resultado em termos de .
Qual é o valor de para o qual o campo é máximo? Qual é o valor do campo máximo?
Faça um gráfico de vs para todo .
Ver solução completaQuestão 122
Uma carga elétrica está uniformemente distribuída dentro de uma esfera isolante de raio
. O campo elétrico num ponto , que se encontra a do centro da esfera é de apontando radialmente para fora da esfera. Qual o valor máximo do campo elétrico gerado por esta esfera?
Questão 123
Um cilindro maciço infinito, não condutor, de raio , apresenta uma densidade volumétrica de carga variável dada por :

onde é uma constante positiva e é a distância ao eixo de simetria do cilindro (veja figura abaixo). Nestas condições, calcule:

- A carga elétrica numa porção finita do cilindro, que tenha comprimento .
- O módulo do campo elétrico para .
- O módulo do campo elétrico para .
Questão 124
Dois planos muito grandes, homogeneamente carregados, um com e outro com , estão separados por uma distância como mostra a figura. Assinale a opção que especifica, corretamente, o módulo, direção e sentido do campo elétrico na região I:
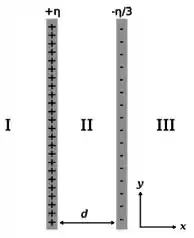
Questão 125
Considere uma casca cilíndrica isolante de altura “infinita”, raio interno e raio externo . Ao longo desse cilindro existe uma carga distribuída homogeneamente com densidade volumétrica não uniforme .
Nota: a figura mostra a seção transversal da casca cilíndrica.
a) Encontre o módulo do campo elétrico na região .
b) Encontre o módulo do campo elétrico fora da casca .
c) Encontre o módulo do campo elétrico dentro da casca, .
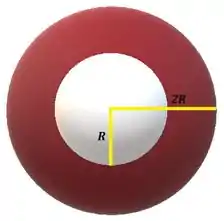
Considere agora que a casca cilíndrica seja envolvida por uma outra casca cilíndrica condutora de raio interno e raio externo . A carga líquida da casca condutora é nula e o sistema já alcançou o equilíbrio eletrostático.
d) Encontre o módulo do campo elétrico na região .
e) Encontre o módulo do campo elétrico na região .
Ver solução completaQuestão 126
Um bastão cilíndrico isolante, de comprimento muito longo e raio (com ), foi carregado com uma densidade volumétrica de carga não uniforme , onde é uma constante. A carga total no bastão é .
O bastão está envolvido por uma casca cilíndrica condutora concêntrica de mesma altura e de raios e , conforme mostra a Figura. A configuração se encontra em condições de equilíbrio eletrostático.
O campo elétrico gerado a uma distância () do eixo de simetria comum é igual a e a carga total na superfície externa (raio ) da casca condutora é .
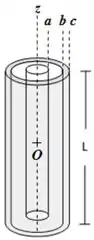
(a) Expresse em função de e do volume do bastão.
(b) Calcule as densidades superficiais de carga e nas superfícies interna e externa da casca condutora, respectivamente. No cálculo de , expresse em função de e da área da superfície externa da casca condutora.
(c) Obtenha o valor (módulo) do campo elétrico em um ponto arbitrário do interior do bastão () e muito afastado de suas extremidades.
(d) Obtenha o valor (módulo) do campo elétrico em um ponto arbitrário situado entre o bastão e a superfície interna da casca condutora () e muito afastado de suas extremidades.
(e) Obtenha o valor (módulo) do campo elétrico em um ponto arbitrário do interior da casca condutora () e muito afastado de suas extremidades.
(f) Obtenha o valor (módulo) do campo elétrico em um ponto arbitrário do exterior da casca condutora () e muito afastado de suas extremidades.
Ver solução completaQuestão 127
Uma esfera de raio possui uma densidade de carga volumétrica uniforme . Considerando
a superfície gaussiana na figura abaixo constituída por um disco circular e um hemisfério. Os dois formam uma superfície fechada e concêntrica com a esfera carregada. Quanto vale o fluxo elétrico sobre a superfície gaussiana?

Questão 128
Um cilindro muito longo de raio possui uma densidade volumétrica de carga uniforme e positiva, . Obtenha uma expressão para o campo elétrico (a) no interior do cilindro (r ≤ a) e (b) fora do cilindro(r > a). Assuma que o cilindro seja feito de material não-condutor.
Ver solução completaQuestão 129
Um cilindro muito longo de raio possui uma densidade volumétrica de carga uniforme e positiva, . Obtenha uma expressão para o campo elétrico (b) fora do cilindro(r > a). Assuma que o cilindro seja feito de material não-condutor.
Ver solução completaQuestão 130
Uma camada esférica feita de um material não condutor de raio interno e raio externo tem densidade volumétrica uniforme de carga
na região (veja a Figura 3), onde é uma constante positiva. Determine expressões para o campo elétrico nas regiões: (a) r b.
Ver solução completaQuestão 131
Uma camada esférica feita de um material não condutor de raio interno e raio externo tem densidade volumétrica uniforme de carga
na região (veja a Figura 3), onde é uma constante positiva. Determine expressões para o campo elétrico nas regiões: (a) r b.
Ver solução completaQuestão 132
Uma camada esférica feita de um material não condutor de raio interno e raio externo tem densidade volumétrica uniforme de carga
na região (veja a Figura 3), onde é uma constante positiva. Determine expressões para o campo elétrico nas regiões: (a) r b.
Ver solução completaQuestão 133
(Capítulo 23 – Problemas Adicionais – Exercício 76) Um cilindro muito longo de raio R possui uma distribuição volumétrica de cargas uniforme. (a) Mostre que, a uma distância r