Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 13.6 - Ex. 49
Um cometa que foi visto em abril de 1574 por astrônomos chineses, em um dia conhecido como Woo Woo, foi avistado novamente em maio de 1994. Suponha que o intervalo de tempo entre as observações seja o período do cometa e tome a sua excentricidade como sendo . Quais são (a) o semi-eixo maior da órbita do cometa e (b) a sua maior distância ao Sol em termos do raio médio da órbita de Plutão, ?
Passo 1
(a) Queremos encontrar o semi-eixo maior da órbita, tendo apenas o seu período e excentricidade. Vamos relembrar a 3ª lei de Kepler:
Em que é a massa do Sol, e é o semi-eixo maior da elipse que descreve a órbita (quando a órbita é circular esse vira simplesmente o raio da órbita).
Além disso, a questão pediu para considerarmos o tempo entre as aparições como o período de revolução do cometa, então:
Convertendo de anos para segundos:
Passo 2
Consultando a massa do Sol em uma tabela e substituindo tudo na equação:
Pronto, já encontramos o semi-eixo maior.
Passo 3
No item (b), queremos saber qual é a maior distância entre o cometa e o sol. Vamos ver o que está acontecendo:
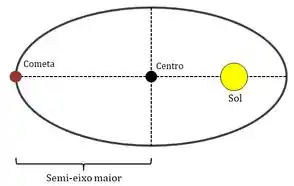
Pela 1ª lei de Kepler, sabemos que se o cometa está orbitando o Sol, então o Sol ocupa um dos focos da elipse que descreve a órbita. A física acaba aqui, agora precisamos de geometria plana.
Vamos lembrar da seguinte relação na elipse:
Substituindo com o que encontramos, e o dado no enunciado:
Por algum motivo o enunciado resolveu pedir a resposta em termos do raio da órbita de Plutão. Olhando uma tabela temos , uma regra de três simples dá:
Pronto!
Resposta
(a)
(b)