Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 99
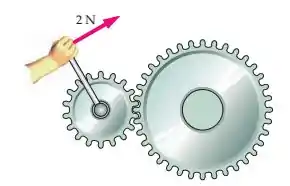
Duas grandes engrenagens estão sendo projetadas como parte de uma grande máquina, como mostrado na figura; cada uma é livre para girar em torno de um eixo fixo que passa pelo seu centro. O raio e o momento de inércia da engrenagem menor são e , respectivamente, e o raio e o momento de inércia da engrenagem maior são e , respectivamente. A alavanca presa à engrenagem menor tem de comprimento e massa desprezível. (a) Se um trabalhador aplica, tiplicamente, uma força de na extremidade da alavanca, como mostrado, quais serão as acelerações angulares das duas engrenagens? (b) Outra parte da máquina (não mostrada) aplica uma força tangencialmente à borda externa da engrenagem maior, para impedir, temporariamente, o sistema de engrenagens de girar. Qual deve ser a magnitude e o sentido (horário ou anti-horário) desta força?
Passo 1
a) Queridooo, cê tá bem? Vamos refletir aqui nessa questão.
Ele quer saber a aceleração angular de cada uma das engrenagens. Ele diz para gente que um trabalhador aplica uma força de na borda da engrenagem menor.
Cara, se fala de aceleração angular e força aplicada, cê pode pensar logo em segunda lei de Newton para rotação. Por que? Porque ela tem essa cara:
Onde , que é o torque resultante, vai depender das força aplicadas no nosso sistema.
E se tem segunda lei de Newton precisa ter o melhor amigo dela: o diagrama de corpo livre. Para cada engrenagem, vamos ter:
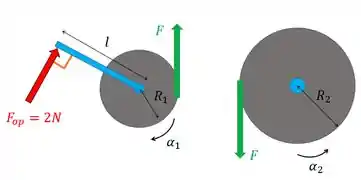
O que está acontecendo ali?
Bem, a força que o trabalhador aplica gera um torque na engrenagem da esquerda, aí a engrenagem roda e entra contato com a engrenagem da direita. A força que ela aplica nessa engrenagem fica no sentido que o torque tem no ponto de contato, ou seja, para baixo.
E a engrenagem da direita gera uma força de reação na outra engrenagem de mesmo módulo, mas sentido inverso.
A gente não colocou a força peso de cada engrenagem porque a força peso tem linha de ação passando pelo CM das engrenagens, então ela não gera torque. Como a gente só vai usar a segunda lei de Newton para rotação, só importa as forças que geram torque, aí não aparece ali, tá?
Bora!
Passo 2
Vamos usar a segunda lei de Newton para a a engrenagem da esquerda:
Vamos chamar a aceleração angular dela de e o momento de inércia dela. O torque resultante vai ser a diferença entre o torque gerado pela força , que vale , já que é a distância da força e o eixo de rotação. E o torque gerado por , que vale .
A gente vai deixar o torque de negativo porque ele está oposto a aceleração da engrenagem que está no sentido do torque de . Então a lei fica:
Substituindo nossos dados:
Passo 3
Aí agora vamos aplicar para a engrenagem da direita:
O único torque sobre ela é gerado pela força , e ele vale . Já que e são perpendiculares, e é a distância entre o ponto de aplicação de o eixo de rotação. Então temos:
Substituindo os dados:
Passo 4
Como as engrenagens andam juntas sem escorregar, as acelerações tangenciais (a aceleração de um ponto qualquer na borda da engrenagem) têm que ser iguais!
Só que podemos escrever a aceleração tangencial , pela expressão . Aí fazendo isso para cada engrenagem e substituindo na relação acima:
Passo 5
Temos 3 equações:
Igualando as duas expressões de :
Substituindo a equação aqui:
Isolando quem a gente quer:
E pela equação (3), podemos achar:
Passo 6
b) Para contrabalancear o torque feito pelo operário, vamos ter que achar um torque igual a ele, mas no sentido oposto! Olha lá pros dentinhos da engrenagem: a menor faz a maior girar no sentido anti horário. Então o torque que tem que aparecer vai ser no sentido horário!
O torque gerado pelo operário é . E o torque gerado por uma força aplicada tangencialmente na engrangem maior vai ser . A gente quer que o módulo desses dois sejam iguais:
Substituindo os dados
E ele está sentido horário!
Obs: O gabarito do livro nessa diz , mas essa seria a resposta aplicando a força na engrenagem menor, já que ficaria: . Como o enunciado fala que vai aplicar na engrenagem maior, devemos colocar na conta. Então estamos certinhos, tá?
Resposta
- , .
- , no sentido horário.