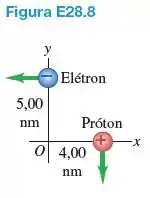
Um elétron e um próton se movem a cada um, em trajetórias perpendiculares, como indica a Figura E28.8. No instante em que eles estão nas posições indicadas na figura, determine o módulo, a direção e o sentido: (a) do campo magnético total que eles produzem na origem; (b) o campo magnético que o elétron produz no local do próton; (c) a força elétrica total e a força magnética total que o elétron exerce sobre o próton.
Passo 1
E aiiii gente, tudo bom com vocês??
Vamos fazer mais uma questãozinha aqui.
Vem comigo!
O enunciado pede pra gente trabalhar com campos magnéticos, forças elétricas e magnéticas em vários pontos. Precisamos lembrar de algumas relações O campo magnético devido a uma carga em movimento é dado pela expressão:
A força elétrica entre cargas elétricas pode ser calculada por:
A força magnética é dada por:
Além disso, o enunciado informa que as trajetórias entre o elétron e o próton são perpendiculares entre si, e eles possuem uma velocidade de:
Ou seja:
Vamos ao ataque!
Passo 2
Na letra (a), precisamos calcular o campo magnético total produzido pelas cargas, na origem! Ambos os campos estão na página, então suas magnitudes somam, da seguinte maneira:
Como ambas estão perpendiculares entre si, e também perpendiculares aos eixos e , o ângulo é ! Além disso, como são cargas com sinais opostos, o vetor campo magnético será a soma do vetor resultantes na origem. O elétron, pela regra da mão direita, produz um campo entrando no plano , na origem. O próton, pela regra da mão direita, também produz um campo entrando no plano , na origem. Dessa forma, o modulo é dado por:
Simplificando, temos:
Pela imagem, sabemos que:
E que:
Substituindo os valores, temos:
Simplificando nossa expressão, temos:
Com sentido para dentro da página!
Passo 3
No item (b), precisamos encontrar o campo magnético que o elétron irá produzir na posição do próton. Com isso, precisamos encontrar a distância entre o elétron e o próton. Vamos esquematizar:
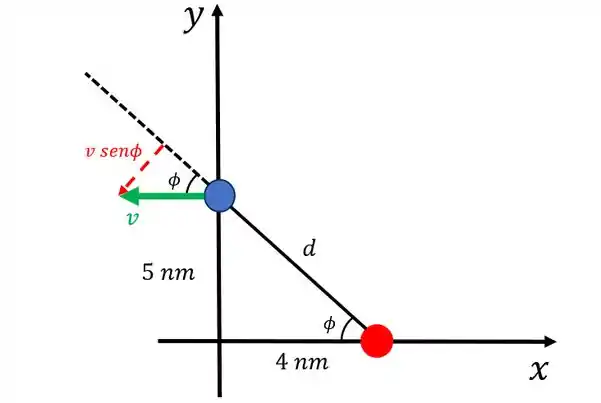
Repare que a distância entre as duas partículas agora é formada pela reta que une os dois. Podemos encontrar o valor fazendo Pitágoras:
Repare que a distância será dada em nanômetros!
Perfeito! Agora que sabemos a distância, repare que a velocidade do elétron com relação a reta que une as duas partículas forma um ângulo que é o mesmo ângulo que de inclinação de com relação a horizontal! Dessa forma, temos que:
Com isso, temos:
O sentido do campo magnético é dado pela regra da mão direita. Como o elétron é uma carga negativa, orientamos a regra da mão direita no sentido oposto de sua velocidade. Com isso, o campo magnético está entrando no plano no próton! Seu módulo será:
Simplificando a expressão temos:
O módulo do campo magnético produzido pelo elétron é:
Com o sentido para dentro da página!
Passo 4
No item (c), devemos calcular a força elétrica e a força magnética produzida pelo elétron sobre o próton. Para a força elétrica, precisaremos apenas usar a distância que encontramos anteriormente. Dessa forma, teremos:
Substituindo as informações, temos:
Simplificando a expressão, temos:
Essa força é atrativa e está na direção de e aponta na direção do elétron!
Para a força magnética, temos:
Repare que precisamos saber , que é justamente o que vimos na questão anterior. Substituindo as informações, temos:
Resolvendo essa expressão, temos:
Como o campo é perpendicular a página e sua velocidade (do próton) é vertical para baixo, pela regra da mão direita, a força magnética será dada na direção e sentido de !
Resposta
- para dentro da página
- e