Exercícios de Campo Magnético Gerado por um Fio - Lista de Exercícios Resolvida
Questão 1
A figura abaixo mostra, em seção reta, quatro fios finos paralelos, retilíneos e muito compridos, que conduzem corrente iguais nos sentidos indicados.
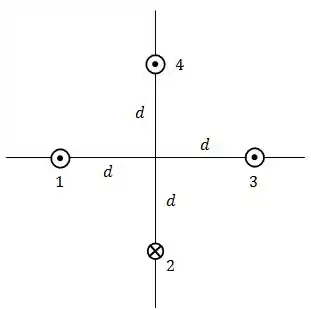
Inicialmente, os quatro fios estão a uma distância da origem do sistema de coordenadas onde criam um campo magnético total .
Para que valor de o fio 1 deve ser deslocado sobre o eixo para que o campo sofra uma rotação de no sentido anti-horário?
Com o fio 1 na nova posição, para que valor de o fio 3 deve ser deslocado sobre o eixo para que o campo volta à orientação inicial?
Ver solução completaQuestão 2
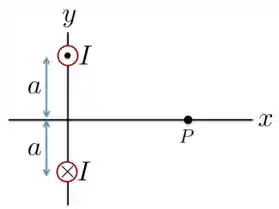
A Figura abaixo representa o plano que corta perpendicularmente dois fios longos (infinitos) e paralelos que conduzem uma corrente , de mesmo módulo, porém de sentidos contrários.
- Copie o diagrama e desenhe os vetores para mostrar que o campo magnético de cada fio e campo resultante no ponto .
- Deduza uma expressão para o módulo do campo em qualquer ponto do eixo em termos da coordenada do ponto. Qual é a direção e o sentido de ?
- Para qual valor de o módulo de atinge seu valor máximo?
- Qual é o módulo de quando ?
Questão 3
Dois fios retilíneos muito longos, paralelos, a uma distância de entre si, transportam, cada um, uma corrente elétrica estacionária de . O módulo da força magnética por unidade de comprimento que cada um exerce sobre o outro é:
.
.
.
.
.
Ver solução completaQuestão 4
Na figura abaixo cinco fios paralelos longos no plano estão separados por uma distância .
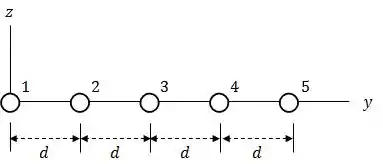
As correntes para dentro do papel são , , e , a corrente para fora do papel é Qual é o módulo da força por unidade de comprimento que age sobre o fio 3?
Ver solução completaQuestão 5
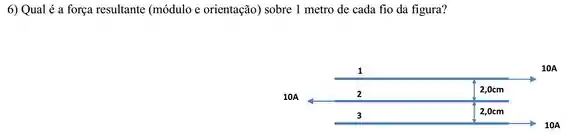
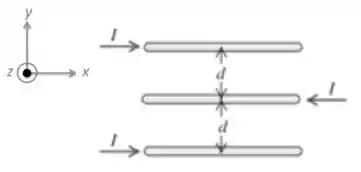
Três fios paralelos e muito longos conduzem correntes de módulo igual a , com os sentidos indicados na Figura abaixo. Sabendo que a distância entre dois fios adjacentes é igual a , calcule o módulo, a direção e o sentido da força magnética resultante por unidade de comprimento sobre cada fio.
Questão 6
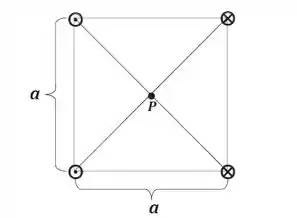
Quatro longos fios são dispostos ortogonalmente ao plano da página, como mostra a figura abaixo, sendo cada um deles percorrido, no sentido indicado, por uma corrente . Determine o vetor resultante no centro do quadrado.
Questão 7
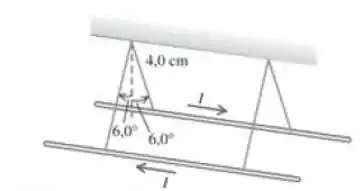
Dois fios longos e paralelos estão suspensos por meio de cordas de de comprimento, presas a um eixo comum, como mostra a Figura abaixo. Os fios possuem massa por unidade de comprimento igual a e conduzem correntes de mesmo módulo, porém de sentidos contrários. Qual é a corrente em cada fio, sabendo que as cordas de sustentação formam um ângulo de com a vertical?
Questão 8
Na figura abaixo, quatro fios retilíneos longos são perpendiculares ao papel, e suas seções retas formam um quadrado de lado .
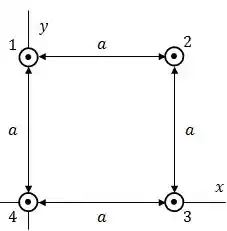
Todos os fios conduzem correntes de para fora do papel. Em termos dos vetores unitários, qual é a força magnética por metro de fio que age sobre o fio 1?
Ver solução completaQuestão 9
Na figura abaixo, dois fios retilíneos longos são perpendiculares ao plano do papel e estão separados por uma distância .
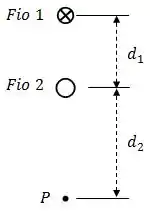
O fio 1 conduz uma corrente de para dentro do papel. Determine o módulo e o sentido (para dentro ou para fora do papel) da corrente no fio 2 para que o campo magnético seja zero no ponto , situado a uma distância do fio 2.
Ver solução completaQuestão 10
Uma espira retangular no plano , de autoindutância desprezível, tem lados e e resistência . Um fio retilíneo infinito, por onde flui uma corrente dependente do tempo , é colocado ao longo do eixo a uma distância da espira, conforme mostra a figura. Despreze as correntes de deslocamento do sistema.
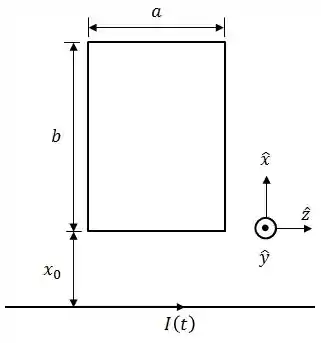
Sabendo que o campo produzido pelo fio retilíneo em um ponto é dado por , onde é a distância de ao fio e é o vetor unitário que “circula” em torno do fio, encontre .
Calcule o fluxo magnético através da espira, tomando como o unitário normal à superfície.
Supondo que , determine a força eletromotriz induzida na espira?
Ver solução completaQuestão 11
Infinitos fios condutores retilíneos, de comprimento infinito e seção transversal quadrada, são colocados lado a lado no plano , de forma compacta e paralelamente à direção . Cada fio conduz uma corrente (no sentido ) e há fios por unidade de comprimento transversal.
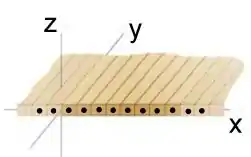
Qual das seguintes afirmações é correta?
O campo magnético aponta na direção e sentido de para e de para e seu módulo é .
O campo magnético aponta na direção e sentido de e seu módulo é .
O campo magnético aponta na direção e sentido de para e de para e seu módulo é .
O campo magnético aponta na direção e sentido de para e de para e seu módulo é .
O campo magnético aponta na direção e sentido de para e de para e seu módulo é .
Ver solução completaQuestão 12
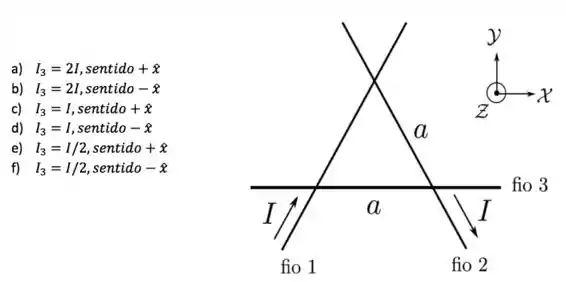
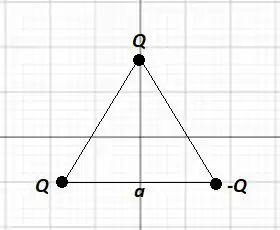
Três fios condutores finos, retilíneos e infinitos são dispostos sobre o plano de um sistema de coordenadas, de forma que um deles é paralelo ao eixo e a região definida pela interseção dos três fios é um triângulo equilátero de lado , como mostrado na figura abaixo. Dois destes fios carregam correntes estacionárias de mesma intensidade e sentidos indicados na figura. Quais devem ser a intensidade e o sentido da corrente estacionária no terceiro fio para que o campo magnético no centro do triângulo seja nulo?
Questão 14
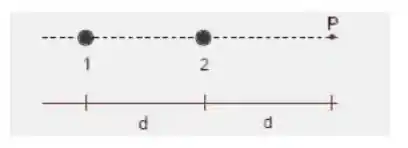
A figura abaixo representa dois fio bastante longos (1 e 2) perpendiculares ao plano do papel, percorridos por correntes de sentido contrário, e , respectivamente. A condição para que o campo magnético resultante, no ponto , seja zero é:
Questão 15
Em uma região do espaço existe um campo magnético na direção cuja magnitude é função da posição no como:
 a) Nessa região do espaço, colocamos um segmento linear de comprimento L percorrido por
a) Nessa região do espaço, colocamos um segmento linear de comprimento L percorrido por
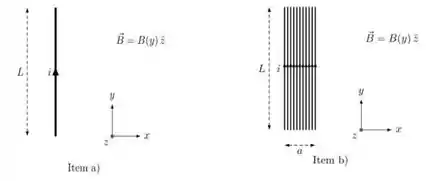
uma corrente i. O segmento está orientado como mostra a figura, paralelo ao eixo-y com seu ponto inferior em y=0. Calcule o vetor força magnética total sentido pelo segmento.
b) Considere um sistema composto de vários segmentos (ao invés de apenas um) de mesmo tamanho L muito finos e colocados um do lado do outro formando uma parede de segmentos com largura a como mostra a figura. A corrente total que atravessa esse sistema é i e agora está distribuída igualmente entre os segmentos. Qual é o valor do vetor força magnética sentido pelo sistema?
Ver solução completaQuestão 16
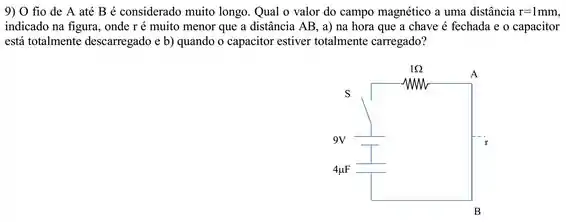
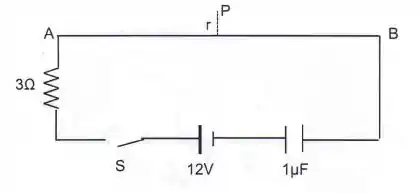
No circuito abaixo, o fio de até é considerado muito longo e a distância muito menor do que a distância . O capacitor está inicialmente descarregado. Qual o valor do campo magnético no ponto a uma distância , indicado na figura, imediatamente após a chave ser fechada e quando o capacitor estiver totalmente carregado, respectivamente:
(a)
(b)
(c)
(d)
(e)
Questão 17
Um fio de de comprimento transporta uma corrente de , no sentido positivo do eixo , em uma região do espaço onde um campo magnético uniforme dado por está presente. Qual é o vetor força magnética resultante que atua no fio?
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 18
Sejam dois fios longos retilíneos que conduzem correntes estacionárias de mesma intensidade e mesmo sentido. Eles são paralelos entre si e estão separados por uma distância , conforme a figura.
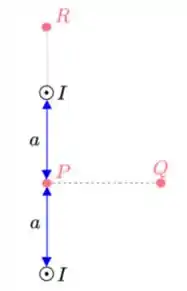
Podemos dizer que o sentido do campo magnético resultante nos pontos P, Q e R (quando não nulo) é:
a) P: para direita; Q: para baixo; R: para direita.
b) P: nulo; Q: para cima; R: para esquerda.
c) P: nulo; Q: nulo; R: para cima.
d) P: para esquerda; Q: para baixo; R: nulo.
e) P: nulo; Q: para baixo; R: nulo.
Ver solução completaQuestão 19
Uma corrente i percorre um fio muito longo. O fio está posicionado inicialmente de maneira vertical. Em certo ponto, realiza um loop circular de raio e retorna à mesma orientação vertical, como mostra a Figura 1. Embora extremamente próximos, não há contato entre os pontos inicial e final do loop.
Com relação ao ponto C marcado na figura, calcule, utilizando a lei de Biot-Savart explicitamente:
- O vetor campo magnético devido ao loop.
- o vetor campo magnético devido a cada uma das duas seções retas do fio
- Qual deve ser a relação entre as correntes e para que o torque resultante devido ao campo magnético sobre o conjunto de loops seja nulo?
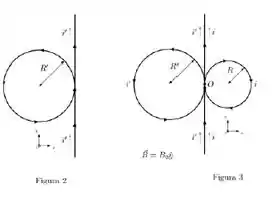
Considere agora outra configuração, onde uma nova corrente i’ percorre um segundo fio também muito longo. Mais uma vez, o fio está posicionado inicialmente de maneira vertical e, em certo ponto, realiza um loop circular de raio , retornado à mesma orientação vertical, como mostra a Figura 2. Embora extremamente próximos, não há contato entre os pontos inicial e final do loop.
Em seguida, esse fio é colocado bem próximo (mais uma vez, sem contato) ao primeiro fio, como mostra a Figura 3. No sistema descrito pela Figura 3, existe um campo magnético constante .
Questão 20
Os quatro fios retos, infinitos e paralelos ao eixo estão dispostos nos vértices de um quadrado de lado e têm correntes de mesmo módulo. Os sentidos das correntes e as posições dos fios estão indicados na Figura. Determinar o vetor campo magnético total (devido a todos os fios) nos pontos:
- de coordenadas .
- de coordenadas .
-
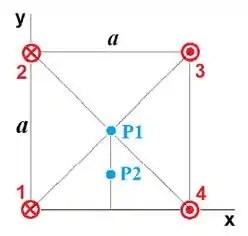
1,2 e sobre o fio .
Questão 21
Dois fios retilíneos muito longos transportam correntes paralelas ao longo da direção um deles transporta a corrente no sentido , e o outro transporta uma corrente . Na figura mostram-se o ponto , de coordenadas , e o campo magnético em devido somente ao fio .
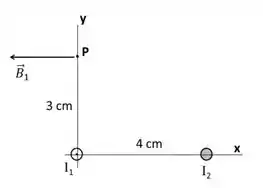
A fim de que o campo resultante no ponto (devido a ambos os fios) possua direção , qual deve ser o sentido e quanto deve valer a corrente ?
Suponha que o campo resultante seja dado por: . Um terceiro fio retilíneo e muito longo transportando corrente no sentido é colocado passando por . Encontre, na unidade , o vetor força por unidade de comprimento que o terceiro fio sofre.
Ver solução completaQuestão 22
Dois fios muito longos dispostos paralelamente transportam a mesma intensidade de corrente e se repelem com uma força por unidade de comprimento de módulo . Se as correntes nos dois fios têm seus valores dobrados e a distância de separação entre os fios é triplicada, qual será o valor da intensidade da força por unidade de comprimento?
Questão 23
Dois fios retilíneos muito longos, paralelos, transportam correntes de mesma intensidade e sentido, conforme a figura abaixo.
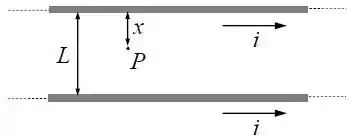
A distância entre os fios é e o ponto encontra-se a uma distância de um dos fios. A intensidade do campo magnético no ponto , e da força magnética por unidade de comprimento, , que um fio exerce sobre o outro são:
Ver solução completa
Questão 24
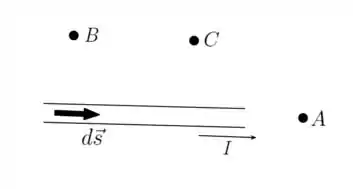
Considere o campo magnético devido à corrente no fio mostrado na figura. Ordene os pontos , e de acordo com o módulo do campo magnético produzido neles pelo elemento de corrente , começando pelo maior.
(a) .
(b)
(c) .
(d) .
(e) .
Ver solução completaQuestão 25
Quatro fios retilíneos e infinitos são paralelos e carregam correntes estacionárias de mesma intensidade , com sentidos indicados na figura abaixo.
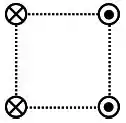
Eles são posicionados de forma que, num corte transversal, ocupam os vértices de um quadrado, como mostrado na figura. Sobre esse sistema, considere as seguintes afirmativas:
O campo magnético no centro do quadrado tem direção vertical e aponta para baixo.
A força magnética resultante sobre qualquer um dos fios tem direção paralela a uma das diagonais do quadrado.
São VERDADEIRAS as afirmativas:
;
;
Todas elas;
Nenhuma delas;
Ver solução completaQuestão 26
Considere um fio retilíneo neutro e infinito e uma partícula (pontual) carregada em repouso, a uma certa distância do fio. Em um determinado instante , surge, no fio, uma corrente não estacionária . Se o fio é o único agente interagindo com a partícula, o que acontece com esta depois do instante ?
- Ela deve permanecer em repouso, pois forças magnéticas não realizam trabalho.
- Ela pode sair do repouso, devido à ação de forças magnéticas.
- Ela deve permanecer em repouso, devido à simetria do problema.
- Ela pode sair do repouso, devido à ação de forças elétricas.
- Ela deve permanecer em repouso, pois o fio é neutro.
Questão 28
Considere um fio longo reto, percorrido por uma corrente elétrica constante. O módulo do vetor indução magnética produzido pela corrente a do fio é igual a . Qual a intensidade do vetor indução magnética a do mesmo fio, quando percorrido pela mesma corrente?
Ver solução completaQuestão 29
Um fio condutor retilíneo e muito longo é percorrido por uma corrente elétrica constante, que cria um campo magnético em torno do fio. Esse campo magnético
- É uniforme
- Diminui a medida que a distância em relação ao condutor aumenta
- Tem o mesmo sentido da corrente elétrico
- É paralelo ao fio
- É perpendicular ao fio e constante
Questão 30
Suponha um fio de cobre, reto e extenso, que é percorrido por uma corrente . Qual é a intensidade do vetor campo magnético originado em um ponto à distância do fio?
Ver solução completaQuestão 31
Considere um condutor reto e extenso , percorrido por uma corrente elétrica de intensidade igual a . Determine, aproximadamente, a intensidade do vetor indução magnético em um ponto a do condutor. Considere e
Ver solução completaQuestão 32
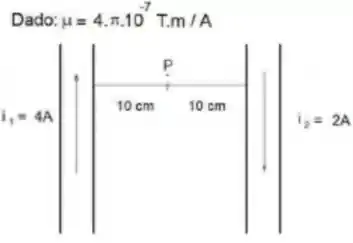
Situados no vácuo existem dois fios longos, retilíneos e paralelos, os quais fluem correntes contrárias, com intensidade e , e separados entre si de uma distancia fixa igual a 2 vezes . Calcule a intensidade do vetor campo magnético resultante no ponto , equidistantes dos referidos fios, conforme indicado na figura abaixo
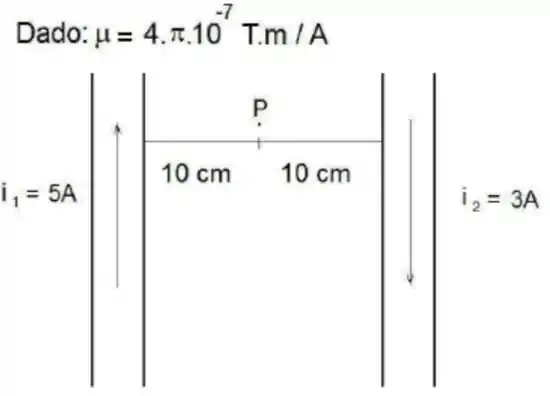
Questão 33
Dois fios longos, retos e paralelos, situados no vácuo, são percorridos por correntes contrárias, com intensidade e , e separadas entre si de . Calcule a intensidade do vetor indução magnética resultante no ponto , equidistante dos referidos fios, conforme indica a figura abaixo
Questão 34
Três fios condutores retilíneos paralelos e com comprimento infinito se encontram no mesmo plano , com o fio condutor central que coincide com o eixo , como mostrado nas figuras abaixo. A distância entre os fios condutores contíguos é . O condutor central é percorrido por uma corrente constante no sentido , enquanto os dois condutores laterais são percorridos cada um por uma corrente no sentido oposto .
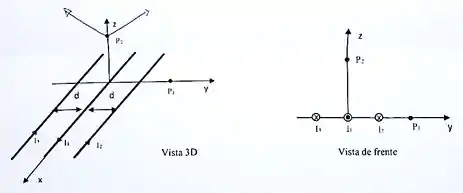
Determine (deixe os cálculos em função de ):
(a) O campo magnético gerado pelos três condutores no ponto com coordenadas .
(b) O campo magnético gerado pelos três condutores no ponto com coordenadas .
(c) A força por unidade de comprimento experimentada pelo condutor central devida ao campo magnético produzido pelos outros dois condutores.
(Sugestão: lembre-se que, por Ampère, o módulo do campo magnético produzido por um fio infinito em uma distância é dado por: ).
Ver solução completaQuestão 35
Considere um fio longo, percorrido por uma corrente com dois trechos retilíneos e um trecho de semicircunferência de raio com centro no ponto , conforme mostra a figura abaixo. O ponto fica a meio caminho dos dois trechos retilíneos e a uma distância muito grande da semicircunferência, de modo que para ele os dois trechos retilíneos podem ser considerados infinitos.
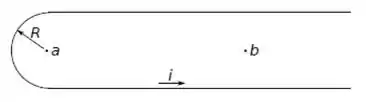
a) Calcule o módulo e o sentido do campo magnético no ponto .
b) Calcule o módulo e o sentido do campo magnético no ponto .
Ver solução completaQuestão 36
13 - Considere dois fios muito longos e retos (veja figura - s é a distância do ponto P a cada fio). Cada fio transporta uma corrente estacionária. O campo magnético (módulo, direção e sentido) produzido no ponto P vale
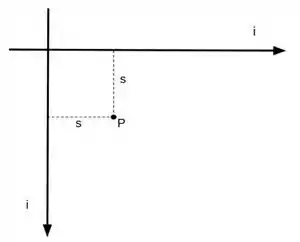
- apontando para dentro da folha.
- apontando para fora da folha.
- apontando para dentro da folha.
- apontando para fora da folha.
- .
Questão 38
Três fios retilíneos e longos, separados a uma distância igual a , são percorrido por uma corrente elétrica igual a . Eles são paralelos e dispostos conforme a figura abaixo. Calcule e indique na figura o vetor campo magnético nos dois pontos, e .
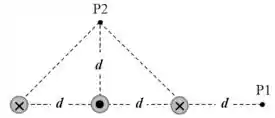
Questão 39
(Capítulo 29.2 – Exercício 21) A figura 29-48 mostra, em seção reta, dois fios retilíneos muito longos, ambos percorridos por uma corrente de orientada para fora do papel. A distância entre os fios é e a distância entre o ponto P, equidistante dos dois fios, e o ponto médio do segmento de reta que liga os dois fios é . Determine o módulo do campo magnético total produzido no ponto P pelos fios.
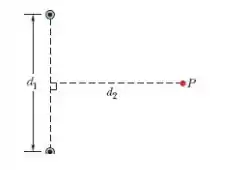
Questão 40
Seja um segmento reto de fio de comprimento , por onde passa uma corrente estacionária de intensidade (suprida por um circuito conectado a este segmento).
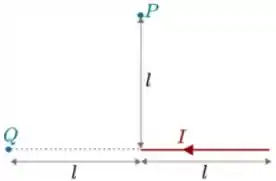
Considere os pontos e dados na figura. A intensidade do campo magnético produzido pelo segmento nestes pontos vale:
Escolha uma:
. e
. e
. e
. e
e. e
Ver solução completaQuestão 41
10) Um fio fino circular, de raio , é percorrido por uma corrente estacionária de intensidade . No mesmo plano, temos um outro fio, constituído por dois segmentos retilíneos longos e um arco de semicircunferência, concêntrico com o primeiro fio, de raio , conforme mostra a figura. Qual deve ser a intensidade da corrente estacionária , nesse segundo fio, para que o campo magnético no centro comum seja nulo?
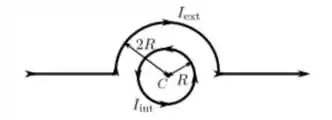
a)
b)
c)
d)
e)
Ver solução completaQuestão 42
Quatro partículas pontuais de cargas se movem com velocidades e , com . Num dado instante, as partículas ocupam os vértices de um quadrado de lado , no plano , como mostrado na figura abaixo.
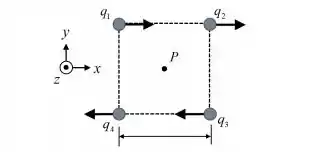
Quais são, respectivamente, o sentido do campo magnético produzido pelas quatro partículas no ponto , localizado no centro do quadrado, e a razão entre os módulos de e o módulo do campo magnético , produzido pela partícula também no ponto ?
(a)
(b)
(c)
(d)
(e) A soma do campo produzido pelas quatro partículas se anula.
Ver solução completaQuestão 43
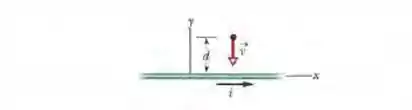
(Capítulo 29.2 – Exercício 23) A figura 29-50 mostra um próton que se move com velocidade em direção a um fio retilíneo longo que conduz uma corrente . No instante mostrado, a distância entre o próton e o fio é . Em termos dos vetores unitários, qual é a força magnética a que o próton está submetido?
Questão 44
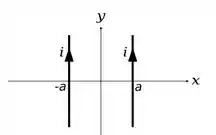
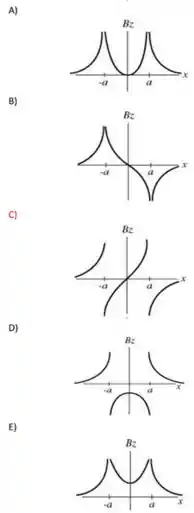
12 - Dois fios muito longos no plano , separados por uma distância , são paralelos ao eixo e transportam correntes iguais , como mostrado na figura. Se ambas as correntes fluem na direção , qual dos gráficos mostrados na figura abaixo melhor representa a componente do campo magnético, no plano , como uma função de ?
Questão 45
A lei de Biot-Savart serve para calcular o campo magnético no ponto C, o centro comum dos arcos semicirculares AD e HJ na figura. Os dois arcos de raios R1 e R2 formam parte do circuito ADJHA, o qual transporta uma corrente elétrica . Qual das seguintes afirmativas é verdadeira?
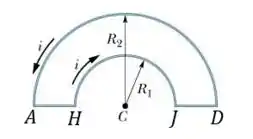
A) Somente os trechos AH e JD contribuem para o vetor campo magnético total.
B) Somente o trecho AD contribui para o vetor campo magnético total, pois o seu raio é maior.
C) Somente o trecho HJ contribui para o vetor campo magnético total, pois o seu raio é menor.
D) O vetor campo magnético total é perpendicular ao plano da página e aponta para dentro da página.
E) O vetor campo magnético total é perpendicular ao plano da página e aponta para fora da página.
Ver solução completaQuestão 46
1ª questão - Qual das alternativas a seguir é uma afirmação correta?
A) As linhas de campo magnético têm como fontes os pólos norte e sul.
B) Uma linha de campo magnético é, por definição, tangente à direção da força magnética sobre uma carga em movimento em um determinado ponto no espaço.
C) Um ímã permanente ao ser cortado ao meio produz dois ímãs menores contendo ambos pólos Norte e Sul em cada ímã.
D) A força magnética em um fio condutor de corrente é maior quando o fio é paralelo ao campo magnético.
E) Uma espira de fio condutora de corrente tende a se alinhar com seu plano paralelo a um campo magnético externo no qual está posicionada.
Ver solução completaQuestão 47
Dois fios longos e paralelos de cobre, com de diâmetro, conduzem correntes de em sentidos opostos. Se os eixos centrais dos fios estão separados por uma distância de , determine o fluxo magnético por metro de fio que existe no espaço entre os fios.
Dados: ;
Ver solução completaQuestão 48
Um fio de cobre de seção reta e comprimento é percorrido por uma corrente de uniformemente distribuída. Calcule:
- O campo magnético médio dentro do condutor
Questão 49
(Capítulo 29.2 – Exercício 7) Na figura 29-38, dois arcos de circunferência têm raios e , subtendem um ângulo , conduzem uma corrente de e têm o mesmo centro de curvatura P. Determine (a) o módulo e (b) o sentido (para dentro ou para fora do papel) do campo magnético no ponto P.
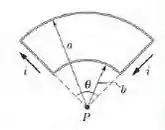
Questão 50
(Capítulo 29.2 – Exercício 29) A figura 29-56 quatro fios retilíneos longos são perpendiculares ao papel e suas seções retas formam um quadrado de lado . As correntes são para fora do papel nos fios 1 e 4 para dentro do papel nos fios 2 e 3 e todos os fios conduzem uma corrente de . Em termos dos vetores unitários, qual é o campo magnético no centro do quadrado?
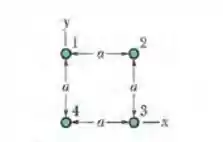
Questão 51
Uma corrente passa em cada um dos três fios retilíneos longos, situados nos vértices de um triângulo equilátero. Os fios são perpendiculares ao plano que contém o triângulo, conforme mostra a figura. Desconsiderando o campo magnético terrestre, a orientação de uma bússola colocada no ponto fica:
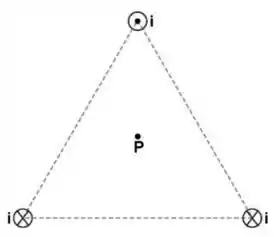
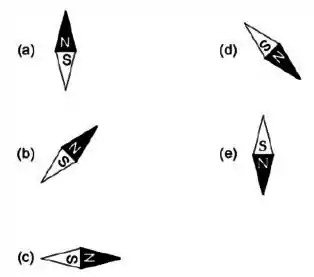
Questão 52
Em seus trabalhos, no ano de 1820, o físico dinamarquês Oersted fez um condutor ser percorrido por uma corrente elétrica e percebeu que a agulha de uma pequena bússola sofria deflexão. Com esta experiência, foi possível mostrar que:
- Uma carga em movimento gera um campo magnético.
- Uma carga em movimento ou não gera um campo elétrico.
- Uma carga em movimento gera um campo elétrico.
- Nenhuma evidência física foi percebida.
- Uma carga em movimento ou não gera um campo magnético.
Questão 53
14 - Uma espira condutora no formato de uma elipse conduz uma corrente . Suficientemente próximo de qualquer ponto da espira, podemos afirmar que:
- Quando estamos muito próximos do fio, podemos aproximar o campo magnético pelo campo no centro de uma espira circular, pois a elipse se aproxima por um círculo.
- O campo magnético é nulo devido ao fato de a lei de Biot-Savart nos dizer que o campo magnético diminui quanto próximo de sua fonte.
- Quando estamos muito próximos do fio, podemos aproximar o campo magnético pelo campo do fio infinito uma vez que a curvatura do fio se torna imperceptível.
- O campo magnético é radial ao fio, como em todo condutor em equilíbrio estático.
- Não há como fazer esse cálculo, pois não há simetria suficiente.
Questão 54
Três cargas pontuais se encontram nos vértices de um triângulo equilátero de lado . O centro do triângulo está na origem de um sistema de coordenadas cartesianas e o plano do triângulo fica no plano . Uma das cargas está no eixo as outras simetricamente nos quadrantes III e IV, como mostra a figura. A carga no eixo assim como a carga no quadrante IV tem o valor e a carga no quadrante IV tem o valor .
(a) Calcule o valor do campo elétrico na origem de coordenadas. Escreva o seu resultado de forma vetorial usando a base .
Ver solução completaQuestão 55
(Capítulo 29.2 – Exercício 5) Na figura 29-36, uma corrente circula em um condutor longo formado por dois trechos retilíneos e uma semicircunferência de raio e centro no ponto . O ponto fica a meio caminho entre os trechos retilíneos e tão afastado da semicircunferência que os dois trechos podem ser considerados infinitos. Determine (a) o módulo e (b) o sentido (para dentro ou para fora do papel) do campo magnético no ponto . Determine também (c) o módulo e (d) o sentido do campo magnético no ponto .

Questão 56
(Capítulo 29.2 – Exercício 15) A figura 29-44 mostra dois fios. O fio de baixo conduz uma corrente e inclui um arco de circunferência com de raio e centro no ponto P, que subtende um ângulo de . O fio de cima conduz uma corrente e inclui um arco de circunferência com de raio e centro também no ponto P, que subtende um ângulo de . Determine (a) o módulo e (b) a orientação do campo magnético para os sentidos das correntes indicados na figura. Determine também (c) o módulo e (d) a direção de se o sentido da corrente for invertido.
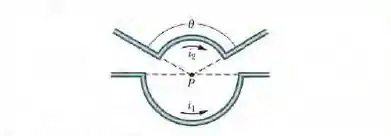
Questão 57
A intensidade da força magnética entre dois condutores retilíneos muito longos e ambos comprimento , dispostos paralelamente um ao outro, afastados de uma distância e percorridos por correntes elétricas de intensidades e , é dada pela equação:
Dois condutores idênticos estão dispostos paralelamente, como mostra a figura. Se a distância entre estes condutores passar a ser o dobro da inicial, eles irão _______________ com uma força de intensidade _________________.

- Repelir-se; .
- Repelir-se; .
- Atrair-se; .
- Atrair-se; .
- Atrair-se; .
Questão 58
1. Considere um condutor cilíndrico de raio , comprimento e condutividade atravessado por uma corrente estacionária . Lembrando que a densidade de corrente pode ser escrita como , determine:
(a) O campo elétrico e magnético dentro e fora do cilindro.
Ver solução completaQuestão 59
1. Considere um condutor cilíndrico de raio , comprimento e condutividade atravessado por uma corrente estacionária . Lembrando que a densidade de corrente pode ser escrita como , determine:
(b) O vetor de Poynting na superfície do cilindro.
Ver solução completaQuestão 60
1. Considere um condutor cilíndrico de raio , comprimento e condutividade atravessado por uma corrente estacionária . Lembrando que a densidade de corrente pode ser escrita como , determine:
(c) A integral do vetor de Poynting sobre a superfície do cilindro.
Ver solução completaQuestão 61
Um solenóide longo de raio é posicionado no interior de um segundo solenóide longo de raio , de forma que seus eixos sejam coincidentes com o eixo de um sistema de coordenadas cartesianas. O número de espiras por unidade de comprimento em cada solenóide vale e , respectivamente. Suponha que os solenóides podem ser tratados como infinitos e que o enrolamento dos fios é compacto. Quando conveniente, considere um segmento de solenóide de comprimento nas análises.
Determine a intensidade do campo magnético produzido pelo solenóide maior em seu interior, quando ele é atravessado por uma corrente estacionária de intensidade .
Ver solução completaQuestão 62
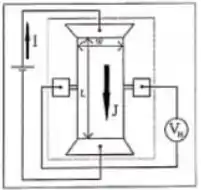
Uma prova Hall como ilustrada na figura permite descobrir propriedades relacionadas à condução elétrica de materiais.
- Explique detalhadamente como o sinal do potencial medido pelo voltímetro nos permite descobrir o sinal das cargas que conduzem uma corrente elétrica de cima para baixo na figura quando temos um campo magnético uniforme entrando na página
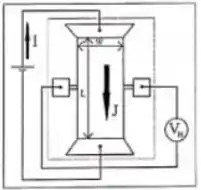
Questão 63
Uma prova Hall como ilustrada na figura permite descobrir propriedades relacionadas à condução elétrica de materiais.
- Se os condutores de eletricidade do material são elétrons com carga que se movimentam com velocidade média (velocidade de arraste), qual é o potencial medido pelo voltímetro se o material tem comprimento por onde passa a corrente , espessura , largura e sob campo magnético ?
Questão 64
Dois fios longos retos paralelos transportam correntes iguais e em sentidos opostos. Em um ponto entre os fios à mesma distância dos dois, o campo magnético que produzem é:
(a) nulo
(b) não nulo, contido no plano formado pelos dois fios e paralelo aos fios
(c) não nulo e fazendo um ângulo menor do que com relação ao plano formado pelos dois fios
(d) não nulo e perpendicular ao plano dos dois fios
(e) não nulo, contido no plano formado pelos dois fios e perpendicular aos fios
Ver solução completaQuestão 65
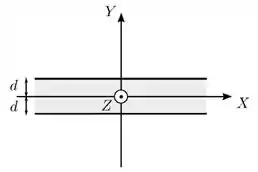
Uma placa condutora infinita de espessura é posicionada de forma que seu plano médio coincide com o plano de um sistema de coordenadas, como mostrado na figura abaixo. Ela possui uma densidade de corrente constante dada por . Nessa situação, o campo magnético produzido pela placa nas regiões e aponta, respectivamente, no sentido dos vetores:
(a) e
(b) e
(c) e
(d) e
(e) e
(f) e
(g) e
(h) e
Ver solução completaQuestão 66
Dois fios condutores, ambos de comprimento , muito longos, transportam correntes estacionárias de intensidades e e estão separados por uma distância , conforme a figura abaixo.
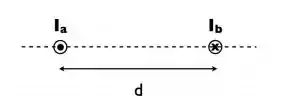
Determine o módulo da força magnética, por unidade de comprimento , entre os fios e diga se a força é atrativa ou repulsiva.
(a) , repulsiva.
(b) , atrativa.
(c) , repulsiva.
(d) , atrativa.
(e) , atrativa.
(f) , repulsiva
Ver solução completaQuestão 67
Uma partícula carregada com carga está se movendo para a direita paralelamente a um fio que conduz uma corrente elétrica também para a direita, como ilustrado na figura.
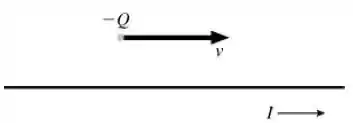
Se a distância da partícula ao fio é muito menor do que o comprimento do fio, a força experimentada pela partícula é:
, na direção vertical, para baixo.
, na direção vertical, para cima.
, na direção vertical, para cima.
, na direção vertical, para baixo.
, na direção vertical, para baixo.
Ver solução completaQuestão 68
O arranjo mostrado na figura abaixo é composto por dois fios retilíneos infinitos, paralelos entre si. Os fios estão separados por uma distância e são perpendiculares ao plano -. Em cada fio passa uma corrente elétrica , apontando nos sentidos indicados na figura.
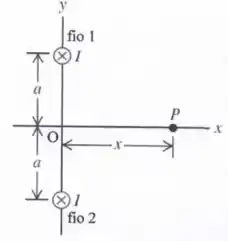
- Copie o diagrama da figura acima e nele desenhe os vetores campos magnéticos gerados pelo fio 1 ( ) e pelo fio 2 () no ponto que dista da origem .
- Calcule o módulo, direção e sentido do campo magnético total no ponto .
- Calcule para que valor de o módulo do campo magnético total é máximo.
- Determine o módulo do campo total quando .
Questão 69
8 - Dois fios retilíneos muito longos transportam uma corrente (a mesma nos dois fios), conforme figura. O ponto P é equidistante de ambos os fios. O campo magnético no ponto P vale
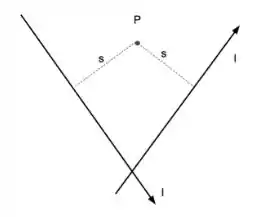
- apontando para dentro da folha.
- apontando para fora da folha.
- apontando para fora da folha.
- apontando para dentro da folha.
- Zero.
Questão 70
2ª questão - Uma espira circular de raio e três longos fios retos conduzem correntes de , , e , respectivamente, como mostrado. Cada fio reto está a do centro da espira. Na Figura abaixo, a componente do campo magnético resultante no centro da espira será:
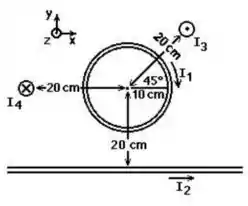
A)
B)
C)
D)
E)
Ver solução completaQuestão 71
Quando uma corrente elétrica circula por um fio, gera ao redor deste um:
- Campo magnético
- Campo elétrico
- Fluxo elétrico
- Pendulo elétrico
- Circuito elétrico
Questão 72
Um elétron em um campo magnético uniforme tem a velocidade . Ele experimenta uma
força. Se Bx = 0 calcule o vetor campo magnético.
Ver solução completaQuestão 73
3.10) Seja um capacitor de placas paralelas e circulares com raio e distância entre as placas
. Considere que há vácuo entre as placas, e que se estabeleça uma voltagem entre elas que
varia no tempo com a forma . Calcule:
(b) O valor máximo atingido pelo campo magnético induzido.
Ver solução completa