Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 11
Dê exemplos de movimento em que os vetores da velocidade e da aceleração têm (a) sentidos opostos e mesma direção, (b) mesma direção e sentido e (c) direções perpendiculares.
Passo 1
(a) Ele quer um exemplo do cotidiano onde velocidade é aceleração tem sentidos opostos mas a mesma direção.
O importante aqui é entender a diferença entre velocidade e aceleração.
A velocidade te diz como a sua posição muda. Ela sempre aponta para o sentido do movimento do objeto. Por exemplo, se a gente tem um carro andando de leste a oeste no uma estrada plana e reta, a velocidade está nesse sentido também.
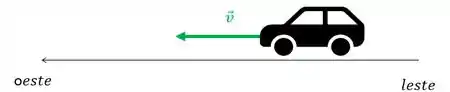
Já a aceleração fala de quanto essa velocidade aumenta ou diminui. Se a velocidade do objeto aumenta, então a aceleração está no sentido do movimento do objeto, mas se a velocidade diminui, então a aceleração é oposta ao sentido do objeto, e assim, oposta a velocidade.
Pera! Lembra que o enunciado pediu uma situação onde aceleração e velocidade são opostas? Acabamos de ver que para isso acontecer, a velocidade do objeto precisa estar dimiuindo.
Que situação do cotidiano a gente pode pensar onde isso acontece? É só imaginar um carro viajando em uma estrada que aponta para oeste (como a nossa ali do desenho), mas que está freando! Assim, a velocidade dele está diminuindo.
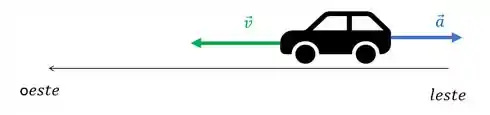
Então um exemplo para a letra (a) seria um carro andando em uma estrada reta enquanto freia.
Passo 2
(b) E a mesma lógica vale para a segunda pergunta. Queremos que aceleração e velocidade estejam no mesmo sentido. Para isso, a velocidade precisa estar aumentando.
Que situação cotidiana retrata isso?
Imagine um carro viajando para o oeste em uma estrada reta, e que está acelerando no mesmo sentido!
Nesse caso a velocidade e a aceleração têm a mesma direção e sentido: ambas apontam para o oeste.
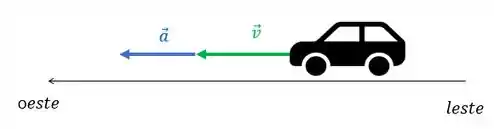
Então temos um carro que acelera e se movimenta no mesmo sentido em uma estrada reta.
Passo 3
(c) Quando o vetor da aceleração é perpendicular ao da velocidade, ela age como uma aceleração centrípeta, e tende a produzir um movimento circular. Assim:
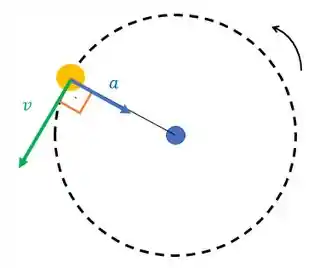
E então um bom exemplo de situação em que esses vetores são perpendiculares é o caso uma partícula se movendo em um círculo com rapidez constante.
Pode ser, por exemplo, um carro em uma pista circular, em que o velocímetro sempre indica a mesma rapidez, mas a trajetória circular indica uma aceleração que aponta para o centro dessa trajetória, ou seja, que é perpendicular a sua rapidez.
Resposta
(a) Carro freando em estrada reta.
(b) Carro acelerando em estrada reta.
(c) Carro em pista circular com rapidez constante.