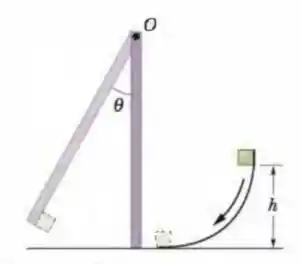
Na Fig. 11-58, um pequeno bloco de desliza para baixo em uma superfície curva sem atrito a partir de uma altura e depois adere a uma barra homogênea de massa e comprimento . A barra gira de um ângulo em torno do ponto antes de parar momentaneamente. Determine .
Passo 1
Show de bolinhas pessoal, primeiro de tudo devemos perceber que antes do impacto a energia mecânica do bloco se conserva. Por isso, vamos aplicar a lei de conservação da energia mecânica para determinar a velocidade com que o bloco alcança a barra:
Isolando obtemos:
Sendo assim, a velocidade com que o bloco atinge a barra é dada como:

Passo 2
A malandragem agora, é que quando o bloco atinge a barra e adere a ela, eles se tornam um conjunto barra-bloco, de modo que o momeno de inércia do conjunto vai ser a soma dos momento de inércia de cada em relação ao eixo de rotação:
Então saca só, o momento de inércia de uma barra cujo o eixo de rotação passa por uma de suas extremidades é:
E supondo o bloco sendo uma partícula de massa , a uma distância do eixo de rotação, temos que seu momento de inércia será:
Sendo assim, o momento de inércia do sistema barra-bloco será:
Substituindo os valores:

Passo 3
Durante a colisão, não há torque resultante, por isso, podemos aplicar a lei da conservação do momento angular:
Nesse caso, o momento angular inicial é dado pela velocidade que apenas o bloco possui em relação ao eixo:
Onde é a distância do bloco até o eixo. Já no momento angular final, temos que:
Logo:
Isolando e substituindo os valores:
Passo 4
Agora pra gente poder aplicar a lei da conservação da energia mecânica e descobrir que altura a barra chegou, precisamos antes saber onde tá o centro de massa do sistema, logo:
Substituindo os valores, temos:

Passo 5
Aplicando agora a lei da conservação de energia, temos:
Onde esse pode ser determinado a partir de relações trigonométrias, considerando que nosso referencial nula será a posição do centro de massa inicial. Assim:
Portanto:
Substituindo os valores, temos:
Isolando :
Isolando :
