Exercícios de Colisões com Rotação - Lista de Exercícios Resolvida
Questão 1
Uma barra delgada homogênea e uniforme, de massa e comprimento , é articulada num pino , que passa por uma de suas extremidades, e pode girar sem atrito num plano vertical. Liberada a partir do repouso na posição horizontal, a barra sofre uma colisão elástica com um pêndulo ao passar pela posição vertical, como representa a massa de dimensões desprezíveis presa à extremidade da haste. O pêndulo também pode oscilar em torno do pino, sem atrito, no mesmo plano vertical que a barra. Sabe-se que o pêndulo encontrava-se em repouso antes da colisão com a barra, e que o momento de inércia da barra em relação ao eixo perpenducular ao plano vertical e que passa pelo pino é
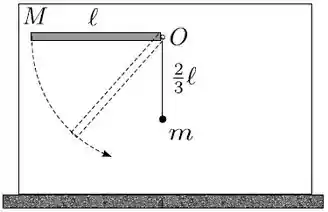
- Determine a velocidade angular da barra, , imediatamente antes da colisão com o pêndulo.
- Quais das seguintes grandezas: o momento linear e o momento angular em relação a são conservadas na colisão? Justifique a sua resposta.
- Determine a velocidade angular da barra, , imediatamente após a colisão.
- Determine o valor da razão para que a barra permaneça em repouso depois da colisão.
Questão 2
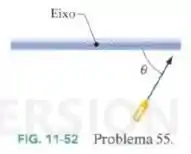
Uma barra fina uniforme com de comprimento e massa pode girar em um plano horizontal em torno de um eixo vertical passando pelo centro. A barra está em repouso quando uma bala de é disparada, no plano de rotação, em direção a uma das suas extremidades. Vista de cima, a trajetória da bala faz um ângulo de com a haste (Fig. 11-52). Se a bala se aloja na barra e a velocidade angular da barra é imediatamente após a colisão, qual é a velocidade da bala imediatamente antes do impacto?
Questão 3
Uma pessoa está com os braços abertos sobre uma plataforma giratória (com atrito desprezível no giro) presa ao chão. Nessa posição, o momento de inércia da pessoa com a plataforma é em relação ao eixo de rotação da plataforma. Um disco uniforme de massa raio é lançado com velocidade e velocidade angular conforme a figura. O disco é agarrado pela mão e para de girar, ficando seu centro a uma distância do centro do sistema pessoa-plataforma, na altura dos braços. Determine:
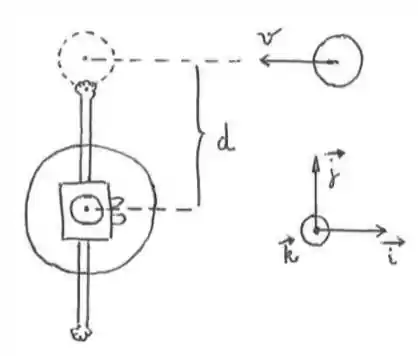
a) O vetor momento angular do disco em relação ao seu centro de massa antes de ser agarrado.
b) O vetor momento angular total do disco em relação ao centro do sistema pessoa-plataforma na altura dos braços, antes de ser agarrado.
c) O momento de inércia do conjunto plataforma-pessoa-disco em relação ao eixo de rotação da plataforma, após o disco ser agarrado.
d) Qual o vetor velocidade angular do conjunto plataforma-pessoa-disco após o disco ser agarrado pela mão? Girará o conjunto no sentido horário ou anti-horário?
Ver solução completaQuestão 4
Uma haste homogênea e uniforme, de espessura desprezível, com massa e comprimento , pode girar sem atrito em torno de um pino que passa por uma de suas extremidades, como mostra a figura. O movimento da haste fica restrito a um plano vertical e o módulo da aceleração local da gravidade é igual a .
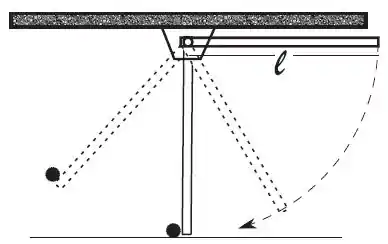
- Sabendo-se que o momento de inércia da haste em relação a um eixo perpendicular à mesma, e que passe pelo seu centro de massa é igual a , calcule o momento de inércia da haste em relação ao eixo de rotação que passa pelo pino.
- Se a haste for liberada na posição horizontal, a partir do repouso, determine sua velocidade angular no instante que passa pela posição vertical.
- Calcule o momento de inércia do sistema haste-corpo após a colisão em relação ao pino.
- Qual é a velocidade angular do sistema haste-corpo de massa , imediatamente após a colisão?
Ainda em relação à situação descrita no ítem anterior, considere que ao passar pela vertical, a exterminadade livre da haste se choque com um pequeno corpo de massa , originalmente em repouso. O corpo de massa adere à haste, e o conjunto continua em movimento de rotação em torno do pino.
Questão 5
Uma haste homogênea e uniforma, de espessura desprezível, com massa e comprimento , pode girar sem atrito em torno de um pino que passa por uma de suas extremidades, como mostra a figura. O movimento da haste fica restrito a um plano vertical e o módulo da aceleração local da gravidade é igual a .
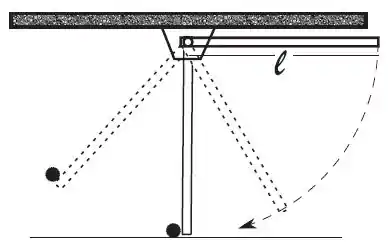
- Sabendo-se que o momento de inércia da haste em relação a um eixo perpendicular à mesma, e que passe pelo seu centro de massa é igual a , calcule o momento de inércia da haste em relação ao eixo de rotação que passa pelo pino.
- Se a haste for liberada na posição horizontal, a partir do repouso, determine sua velocidade angular no instante que passa pela posição vertical.
- Calcule o momento de inércia do sistema haste-corpo após a colisão em relação ao pino.
- Qual é a velocidade angular do sistema haste-corpo de massa , imediatamente após a colisão?
Ainda em relação à situação descrita no ítem anterior, considere que ao passar pela vertical, a exterminadade livre da haste se choque com um pequeno corpo de massa , originalmente em repouso. O corpo de massa adere à haste, e o conjunto continua em movimento de rotação em torno do pino.
Questão 6
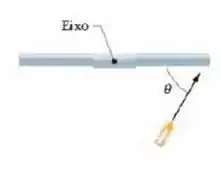
Uma barra fina e homogênea com de comprimento e de massa pode girar em um plano horizontal em torno de um eixo vertical que passa pelo centro da barra. A barra está em repouso quando uma bala de é disparada, no plano de rotação, em direção a uma das extremidades. Vista de cima, a trajetória da bala faz um ângulo com a barra (figura abaixo). Se a bala se aloja na barra e a velocidade da barra é imediatamente após a colisão, qual é a velocidade da bala imediatamente antes do impacto?
Questão 7
Dois discos montados sobre o mesmo eixo podem ser acoplados e girar como se fossem um só. O primeiro disco, com um momento de inercia de em relação ao eixo, é posto pra girar no sentido anti-horário a . O segundo disco, com um momento de inercia de em relação ao eixo, é posto para girar no sentido anti-horário a . Em seguida, os discos são acoplados.
- Qual é a velocidade angular dos discos após o acoplamento?
- Qual é a razão entre as energias cinéticas depois e antes do acoplamento,
- Se o segundo disco fosse posto para girar no sentido horário, qual seria a velocidade angular do conjunto após o acoplamento? Qual seria o sentido de rotação dos discos?
Questão 8
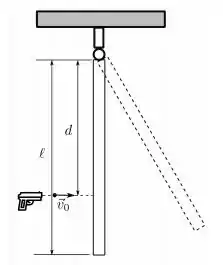
Dois pêndulos estão pendurados no mesmo ponto. Um deles é composto por uma corda de comprimento e massa desprezível e um corpo puntiforme de massa preso à extremidade da corda. O outro pêndulo é composto por uma haste homogênea também de comprimento e massa . O pêndulo formado pela corda e a massa pontual éafastado do equilíbrio até uma altura e liberado de modo a colidir com o outro pêndulo ao atingir a posição vertical. Considerando as leis de conservação relevantes do problema e supondo que o corpo puntiforme fica em repouso após a colisão, a velocidade angular da haste, após a colisão, vale:
- Nenhuma das outras alternativas.
Momento de inércia de uma barra:
Ver solução completaQuestão 9
Uma porta, de largura 0,8 m e momento de inércia (em relação ao eixo das dobradiças) de 4 kg.m², está em repouso e aberta fazendo um ângulo de 90° em relação à parede. Um projétil de massa 5 g é disparado com velocidade de 300 m/s perpendicularmente à porta (a massa do projétil em relação a porta pode ser desprezada). Após o choque, o projétil fica encravado na beirada da porta. Qual é o intervalo de tempo entre o choque do projétil
com a porta e o instante em que a porta se fecha (encosta nos batentes da parede)?
a)
b)
c)
d)
e)
Ver solução completaQuestão 10
A figura mostra uma montagem de laboratório utilizada para experiências de momento angular. Ela é composta por 3 corpos: i) uma haste fina de massa e comprimento articulada por um eixo sem atrito (localizado no ponto P) distante de uma de suas extremidades; ii) uma pequena esfera sólida de massa , presa à extremidade mais próxima ao eixo da haste e iii) um aro de raio e massa preso à outra extremidade. A montagem está girando no plano horizontal com velocidade angular (no sentido horário), quando sofre uma colisão ao se encontrar na posição à acima do eixo com uma esfera sólida de massa que se move com velocidade . A esfera fica presa no aro.
Considere as esferas como pontuais. Utilize: ; .
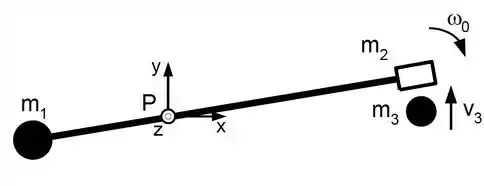
Calcule o momento de inérica de cada componente da montagem em torno do ponto P, formado pela haste fina, esfera de massa e aro.
Calcule o vetor momento angular total do sistema imediatamente antes da colisão (. Responda se haverá ou não conservação do momento angular do conjunto durante a colisão, justificando cuidadosamente.
Calcule o módulo da velocidade angular imediatamente após a colisão e informe também o sentido da rotação do conjunto.
Ver solução completaQuestão 11
Na figura abaixo observa-se uma barra fina uniforme no plano horizontal de massa e comprimento . Ela está inicialmente em repouso e presa a um eixo fora do seu centro de massa que aponta na direção . Este eixo pode girar livremente. Duas partículas idênticas de massa se movimentam paralelamente com velocidade e vão se chocar simultaneamente com a barra nas suas extremidades, como mostra a figura. Após a colisão as partículas ficam grudadas na barra.
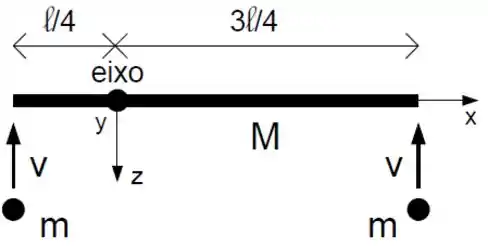
a) Calcule o momento de inércia da barra em relação ao eixo de rotação.
b) Calcule o momento angular do sistema logo antes da colisão em relação à origem.
c) Calcule a velocidade angular do sistema logo após a colisão.
Ver solução completaQuestão 12
Um haltere composto por uma barra delgada de massa desprezível e comprimento L possui em cada extremidade um pequeno corpo de massa de tamanho desprezível. O haltere é colocado para girar sem atrito em torno de um eixo horizontal perpendicular à barra, que passa por um ponto localizado a do seu comprimento. O haltere é abandonado no repouso na posição horizontal (ver desenho). Expresse suas respostas em função de e da aceleração gravitacional .
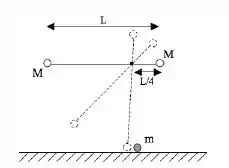
- Calcule o momento de inércia do haltere em relação àquele eixo de rotação.
- Calcule a velocidade linear da extremidade mais comprida do haltere quando ela atinge a posição inferior.
- Se, nesta posição inferior, o haltere colidir com um outro corpo de massa e tamanho também desprezível, inicialmente em repouso e que fica grudado no haltere, qual será a velocidade angular do conjunto logo depois da colisão?
Questão 13
Enunciado das questões (Q4) e (Q5).
O sistema representado ao lado, formado por duas partículas de massas e , ligadas por uma haste em forma de gancho, de massa desprezível e comprimento , pode deslizar sem atrito sobre o plano horizontal . Uma terceira partícula, de massa , movendo-se sobre o plano com velocidade , colide com o sistema formado pelas partículas e , inicialmente parado, ficando presa no gancho.
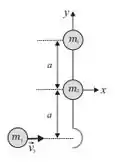
(Q5) [1,0 ponto] Depois da colisão a velocidade angular de rotação do sistema em torno do seu centro de massa é:
Questão 14
A figura a seguir ilustra um objeto A composto por duas partículas de massa (cada), fixadas em uma barra sem massa de comprimento 2D . A figura ilustra também uma barra B. O objeto A e a barra B estão sobre uma mesa horizontal sem atrito e têm uma de suas extremidades conectadas, no ponto O, a um eixo vertical, ao redor do qual podem girar livremente. No instante (ver figura) a barra B está em repouso e o objeto A gira com velocidade angular constante no sentido anti-horário. A distância angular entre eles neste instante é .
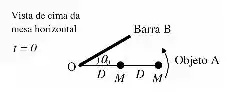
- Em que instante o objeto A e a barra B colidirão?
- Calcule o módulo do momento angular do objeto A em relação ao ponto O no instante .
- Após a colisão, o objeto A e a barra B seguem juntos com velocidade angular . Calcule o momento de inércia da barra B em relação ao eixo vertical passando no ponto O.
Questão 15
Um disco uniforme é montado em um eixo horizontal de massa desprezível, em torno do qual pode girar livremente, como mostra o diagrama. O momento de inércia do disco em relação ao eixo é . O disco está inicialmente girando com velocidade angular ; vide figura. O disco é movimento horizontalmente para esquerda até que sua face entre em contato com um disco idêntico, que está inicialmente em repouso. Depois de um pequeno intervalo de tempo, os dois discos acoplam-se e passa a girar juntos com uma velocidade angular final . Em relação às grandezas: velocidade angular final, energia cinética de rotação e momento angular do sistema, pode-se afirmar que ao final do processo de acoplamento:
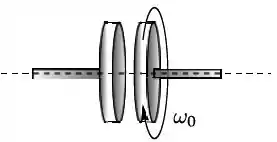
- , não é conservada, não é conservado;
- , é conservada, não é conservado;
- , é conservada, não é conservado;
- , não é conservada, é conservado;
- , é conservada, é conservado;
Questão 16
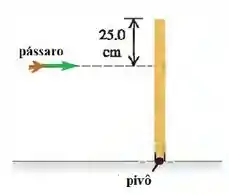
Um pássaro de massa está voando horizontalmente a quando ele subitamente choca-se com uma barra vertical estacionária, atingindo-a abaixo de sua extremidade superior, conforme a figura. A barra é uniforme, tem de comprimento, uma massa e pode girar sem atrito em torno do pivô. Imediatamente após a colisão, o pássaro cai verticalmente. Qual é a velocidade angular da barra imediatamente após ser atingida pelo pássaro? Use: Momento de inércia da barra em relação a um eixo que passa pelo pivô:
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 17
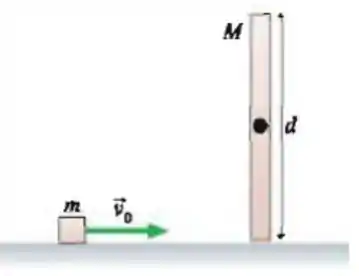
Um cubo de massa m, desliza sem atrito com velocidade . Ele então sofre uma colisão perfeitamente elástica com a extremidade inferior de uma haste de comprimento d e massa M=2m. A haste está presa a um eixo livre de atrito que passa por seu centro e, inicialmente, encontra-se na posição vertical, em repouso.
a) Que grandezas são conservadas na colisão?
b) Qual será a velocidade do cubo, módulo e orientação, após a colisão?
Ver solução completaQuestão 18
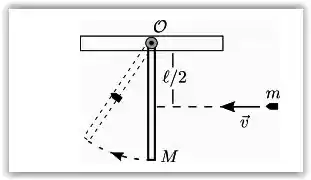
A figura mostra uma barra homogênea de massa M e comprimento que se encontra em repouso na posição vertical, presa ao teto pela sua extremidade superior, podendo girar livremente em um plano vertical em torno de um eixo horizontal OZ (perpendicular ao plano da figura). Um projetil de massa m, e dimensões desprezíveis, move-se no mesmo plano vertical e atinge a barra com velocidade horizontal de modulo v, alojando-se em seu ponto médio. Calcule:
- o momento de inercia da barra relativo ao eixo OZ sabendo que o seu momento de inercia relativo a um eixo ortogonal a ela e que passa pelo seu centro é dado por
- o módulo do momento angular do projétil em relação ao ponto O imediatamente antes da colisão;
- o momento de inercia do sistema barra + projetil relativo ao eixo OZ após a colisão;
d) a velocidade angular adquirida pelo sistema barra + projétil imediatamente após a colisão;
e) a energia mecânica perdida pelo sistema no processo de colisão
Questão 19
Um parquinho possui um pequeno carrossel com de raio e uma massa de . O raio de giração do carrossel (veja o problema 79 do Capítulo 10) é . Uma criança com de massa corre com uma velocidade de em uma trajetória tangente à borda do carrossel, inicialmente em repouso, e pula no carrossel. Despreze o atrito entre os rolamentos e o eixo do carrossel. Calcule (a) o momento de inércia do carrossel em relação ao eixo de rotação, (b) o módulo do momento angular da criança em relação ao eixo de rotação do carrossel e (c) a velocidade angular do carrossel e da criança após a criança saltar no carrossel.
Ver solução completaQuestão 20
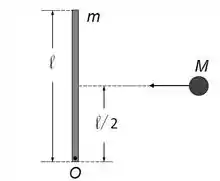
Uma partícula de massa kg move-se inicialmente com velocidade m/s em um plano horizontal sem atrito (ver Figura). Uma barra delgada e homogênea, de massa kg e comprimento m, repousa inicialmente sobre este mesmo plano. A barra pode girar sem atrito ao redor de um eixo fixo, perpendicular ao plano horizontal e que passa pelo ponto numa extremidade da barra. Em um dado instante, a partícula colide com o centro
da barra, perpendicularmente a ela, e fica grudada. O sistema barra + partícula passa então a girar ao redor do ponto .
A velocidade angular do sistema barra + partícula imediatamente após a colisão é:
(a) 0 rad/s
(b) 1,2 rad/s
(c) 2,7 rad/s
(d) 3,6 rad/s
(e) 4,0 rad/s
(f) 4,8 rad/s
(g) 6,0 rad/s
(h) 7,2 rad/s
Ver solução completaQuestão 21
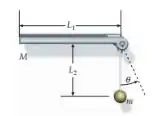
(Cap 10 – Ex 68) Uma barra uniforme, de comprimento igual a e massa igual a , está presa a uma dobradiça de massa desprezível em uma das extremidades e é livre para girar no plano vertical (Figura 10-55). A barra é largada do repouso na posição mostrada. Uma partícula, de massa , está suspensa da dobradiça por um fio fino de comprimento igual a . A partícula gruda da barra quando as duas encostam e após a colisão, a barra continua a gira até . (a) Determine . (b) Quanta energia é dissipada na colisão?
Questão 22
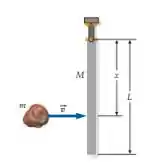
(Cap 10 – Ex 63) A Figura 10-53 mostra uma barra fina e uniforme, de comprimento e massa , articulada na extremidade superior. A barra, que está inicialmente em repouso, é atingida por uma partícula de massa no ponto abaixo da articulação. Suponha que a partícula grude na barra. Qual deve ser a rapidez da partícula, de forma que após a colisão o maior ângulo entre a barra e a vertical seja ?
Questão 23
(Cap 10 – Ex 64) Se, no sistema do Problema 64, , , , e o maior ângulo entre a barra e a vertical após a colisão é , determine a rapidez da partícula antes do impacto.
Ver solução completaQuestão 24
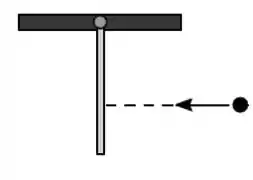
Uma barra está pendurada no teto por um pino em torno do qual pode girar sem atrito. Ela é atingida por uma bola que se move horizontalmente, logo antes da colisão, conforme mostra a figura. A bola está coberta com cola e por isso fica presa à barra. Durante a colisão, qual das seguintes afirmações é verdadeira?
(a) O momento angular do sistema bola + barra, em relação ao pino, se conserva porque nem o pino nem a gravidade exercem torque, em relação ao gancho, sobre o sistema.
(b) O momento angular do sistema bola + barra, em relação ao pino, se conserva porque a única força que age sobre o sistema é a gravidade.
(c) Tanto o momento angular quanto a energia cinética do sistema barra + bola se conservam.
(d) O momento angular do sistema bola + barra, em relação ao pino, não se conserva porque o pino exerce uma força sobre a barra.
(e) Tanto o momento angular quanto o momento linear do sistema barra + bola não se conservam durante a colisão.
Questão 25
A haste de comprimento e massa está livre para girar em torno de um pino fixo na direção do eixo 𝑧. A haste é largada do repouso na posição horizontal e quando chega na posição vertical, sua extremidade inferior colide na altura do centro de massa de um disco de massa e raio . Ele está em repouso sobre uma superfície horizontal com coeficientes de atrito cinético e estático iguais a e respectivamente. Ao final do trajeto a superfície se inclina com um ângulo em relação à horizontal.
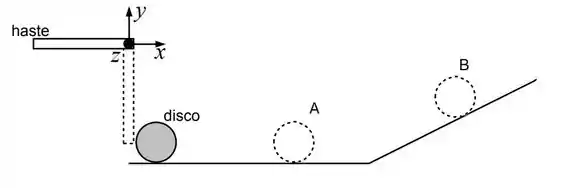
a) Quando a haste chega na posição vertical, imediatamente antes da colisão, sua velocidade na extremidade é . Imediatamente após a colisão o disco tem movimento só de translação com velocidade linear Determine a velocidade linear na extremidade da haste imediatamente após a colisão.
b) Após o deslizamento inicial, o disco passa a rolar sem deslizar ao longo da superfície horizontal com velocidade linear no centro de massa constante . Determine a energia cinética do disco.
c) Desenhe na figura acima todas as forças que agem sobre o disco enquanto ele rola sem deslizar na superfície horizontal (posição A) e enquanto ele sobe a superfície inclinada também rolando sem deslizar (posição B).
d) Determine a altura máxima que o disco alcança em relação à base da superfície inclinada. Justifique sua resposta.
Ver solução completaQuestão 26
Uma barra fina e homogênea de massa e comprimento está pendurada, verticalmente, por sua extremidade superior em um eixo horizontal em torno do qual pode girar sem atrito. Uma bala de massa tem velocidade horizontal de módulo no plano em que a placa pode girar, atinge a barra em repouso a uma distância de sua extremidade superior, e nela fica incrustada, conforme indica a figura.
Nessas condições, o conjunto barra+bala adquire velocidade angular de módulo logo após a colisão e então seu centro de massa eleva-se até uma altura máxima . Sabendo que o momento de inércia da barra relativo ao eixo de rotação é , que e , podemos afirmar que