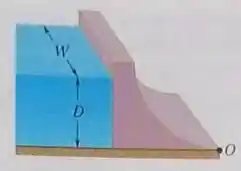
Na Fig. 14-35, a água atinge uma altura atrás da face vertical de uma represa com de largura. Determine (a} a força horizontal a que está submetida a represa por causa da pressão manométrica da água e (b) o torque produzido por essa força em relação a uma reta que passa por O e é paralela à face plana da represa. Determine o braço de alavanca desse torque.
Passo 1
Show de bolinhas pessoal tudo certinho com vocês?
Se liga só, nesse exercício aqui, precisamos lembrar que a força produzida por um fluido sobre uma parede vertical de um recipiente que contém esse fluido, é dada pela integral das infinitas forças que variam com em cada ponto ao longo da altura do líquido.
Uma das formas de calcular a forca exercida pelo fluido sobre a parece vertical indicada na figura é através da soma das componentes de força exercidas pela ação da pressão do líquido nas diversas unidades de área que compõem a superfície da parede, até uma altura de D.
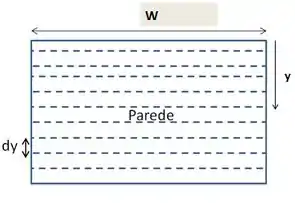
Nesse caso, a força em cada unidade de área é dada por
Como podemos perceber na Figura, cada unidade de área vale:
Logo, as forças exercidas pelo líquido em cada componente de área da parede são expressas assim:
O somatório das infinitas forças que fornece o valor da força total exercida pelo fluido sobre a parede, é dado pela integral da expressão acima
Lembrando que:
Sendo a altura do fluido, nesse problema temos :
Logo:
Passo 2
Então, temos que nossa força sobre a parede é dada como:
Substituindo os valores dados pelo enunciado:
Passo 3
(b) Aqui, precisamos lembrar do conceito de Torque. Lembre-se que ele é obtido pelo produto entre o módulo de uma força e o seu “braço de alavanca”, ou seja, a distância perpendicular à força entre sua linha de ação e o ponto considerado.
Nesse caso, como a força varia com a altura (como já vimos no problema 19), o torque também varia. Cada pequena força de módulo exerce um torque igual a:
Onde y é a altura em que estamos, tomando como referência o ponto O.
Passo 4
Iradoso, então simplificando a fórmula do torque:
E integrando isso de a :
Separando em duas integrais:
Segue que:
Substituindo :
Resolvendo a integral:
Colocando em evidência:
Belezinha, bora lá que ta acabando já hehe
Passo 5
Agora, vamos só simplificar mais um pouquinho:
Substituindo os valores dados pelo enunciado:
Passo 6
Para obtermos o braço de alavanca desse torque, utilizamos o conceito de momento que comentamos na letra (b): . Considerando como igual ao braço pedido, temos:
Sendo e a força e o torque calculados anteriormente. Logo, vem:
Isolando r:
Portanto: