A Fig. 8-39a se refere à mola de uma espingarda de rolha (Fig. 8-39b); ela mostra a força da mola em função da distensão ou compressão da mola. A mola é comprimida e usada para impulsionar uma rolha de . (a) Qual a velocidade da rolha se ela se separa da mola quando esta passa pela posição relaxada? (b) Suponha que, em vez disso, a rolha permaneça ligada à mola e a distenda antes de ocorrer a separação. Qual é, nesse caso, a velocidade da rolha no momento da separação?

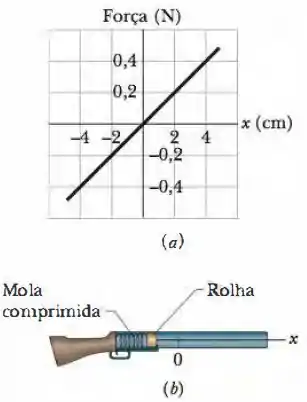
Figura 8-39 Problema 28.

a) Através da inclinação do gráfico da Fig. 8-39a é possível obter a constante elástica da mola ()

Pelo princípio de conservação de energia mecânica

Na posição inicial, não há movimento, logo a energia cinética é nula (). Quando a rolha se separa da mola, esta encontra-se relaxada, o que nos dá energia potencial gravitacional nula (). Dessa forma, a equação se reduz a

Colocando a velocidade em evidência

Para , e