Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 5.Exercícios e Problemas - Ex. 8

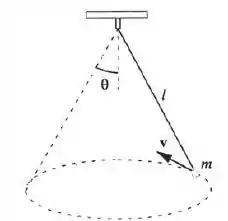
Na Figura 5.12 vê-se uma pedra de massa m , suspensa por um fio, em uma órbita circular em um plano horizontal. A) Identifique as forças que atuam sobre a pedra. B) Qual é a tensão T no fio? C) Qual é a relação entre v e θ ? D) Qual é o período τ da oscilação?

Passo 1

Oi pessoas, tudo certo com vocês? Espero que sim 😊. Nessa questão vamos entender mais como funciona o movimento circular.

Primeiro vamos identificar as forças atuantes no corpo de massa m . Note que esse corpo possui uma força peso, e uma tensão no fio, ou seja,

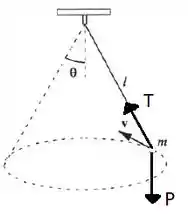
Observe a imagem da questão! Note que, a tensão do fio vai ser igual a força centrípeta. Pois a força centrípeta nada mais é que a força resultante que puxa o objeto para o centro de um movimento circular.

Passo 2

Observe a figura abaixo:

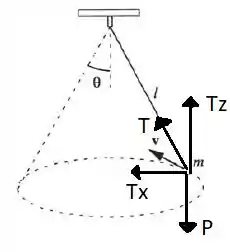
Olhando somente para o plano xy, temos:

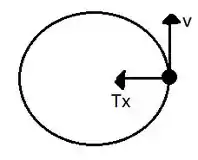
Ou seja, a componente T x podemos representar como uma força centrípeta, ou seja,

T x = m ∙ a c = m ∙ v 2 R

E como,

T x = T ∙ s e n   θ

R = l

Teremos:

T = T x s e n   θ = m ∙ v 2 l ∙ s e n   θ

Passo 3

Certo! Observe na figura onde decompomos as forças de tensão que,

T z = P ∙ s e n   θ

Mas já sabemos que

T z = T ∙ cos ⁡ θ = m v 2 l   s e n   θ ∙ cos ⁡ θ

E como,

P = m g

Temos

m v 2 l   s e n   θ ∙ cos ⁡ θ = m g ∙ s e n   θ  

Organizando,

v = g ∙ l cos ⁡ θ   s e n   θ

Passo 4

Note que,

v = w ∙ R

E como,

w = 2 π τ

Logo,

v = 2 π τ ∙ R

Aplicando a equação que encontramos anteriormente,

τ = 2 π ∙ l ∙ cos ⁡ θ g l = 2 π l cos ⁡ θ g  

Resposta

B )   T = m ∙ v 2 l ∙ s e n   θ  

C )   v = g ∙ l cos ⁡ θ   s e n   θ

D )   τ =   2 π l cos ⁡ θ g  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em que latitude λ o ângulo de desvio entre a direção de um fio de prumo e a direção radial verdadeira (que aponta para o centro da Terra) é máximo? Quanto vale o ângulo de desvio máximo?
Imagine que o quilograma-padrão seja colocado no equador terreste, onde se move em uma circunferência de raio 6,40 × 10 6m (raio da Terra) com uma velocidade escalar constante e 465m / s devido à rota
103- Uma corda pode suportar uma tração máxima de 40 N sem se partir. Uma criança amarra uma pedra de 0,37 kg em uma das extremidades da corda e, segurando a outra extremidade, faz a pedra girar em um
15. Um vagão de montanha-russa passa pelo topo de um loop vertical e circular com velocidade duas vezes maior do que a velocidade crítica. Qual é a razão entre a força normal e a força gravitacional?
16. A força normal iguala-se em intensidade à força gravitacional quando um vagão de montanha-russa passa pelo topo de um loop vertical com 40m de diâmetro. Quanto vale a velocidade do vagão no topo?