Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 10.9 - Ex. 53
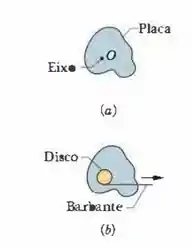
Na figura (a) abaixo, uma placa de plástico de forma irregular, com espessura e massa específica (massa por unidade de volume) uniformes, gira em torno de um eixo perpendicular à face da placa passando pelo ponto O. O momento de inérica da placa em torno desse eixo é medido usando o seguinte método: um disco circular de massa 0,500 Kg e raio 2,00 cm é colado na placa, com o centro coincidindo com O, figura (b). Um barbante é enrolado na borda do disco como se o disco fosse um pião e puxado durante 5,00 s. Em consequência, o disco e a placa são submetidos a uma força constante de 0,400 N, aplicada pelo barbante tangencialmente à borda do disco. A velocidade angular resultante e 114 rad/s. Qual é o momento de inércia da placa em relação ao eixo?
Passo 1
Belezoca galerinha bonita, sabemos que energia cinética de rotação é calculada por:
Enquanto que o torque resultante é dado como:
Combinando as duas equações, descobrimos que:
E para o cálculo da velocidade angular, podemos usar a equação:
Como a velocidade inicial é zero , obtemos que:
Juntando tudo isso, descobrimos que:
Isolando o momento de inércia total , vamos obter:
Passo 2
E como a placa é colocado sobre o disco, o momento inércia total do conjunto disco-placa é dado como a soma dos momentos de inércia individuais, tal que:
Onde o momento de inércia do disco pode ser calculado através da fórmula:
Sendo assim, o momento de inércia da placa será dado como:
Subsituindo pelos valores que o enunciado nos fornece, descobrimos que:
