Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 12.5 - Ex. 21
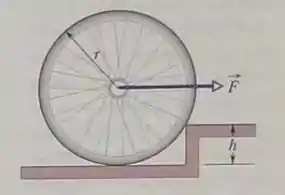
Na figura, qual é o menor valor do módulo da força horizontal constante aplicada horizontalmente ao eixo da roda que permite à roda ultrapassar um degrau de altura ? O raio da roda é e a massa é .
Passo 1
Belezoca galerinha, primeiro de tudo, a gente pode fazer um desenho das forças que atuam na roda, tal que:
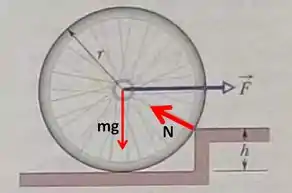
Onde representa a força peso da roda, é a força que exercemos sobre a roda afim de fazer a roda subir o degrau, enquanto é a força normal que piso superior do degrau exerce sobre a roda. Mas ai você me pergunta, porque não temos uma força normal no piso superior?!
Mas calma lá chefia, porque isso ocorre devido ao fato da roda estar na iminência de subir o degrau, nesse caso a roda irá perder o contato com o piso inferior, e se não há contato, não há força normal. Então como estamos trabalhando no caso iminente da roda subir o degrau, a força normal do piso inferior é desprezível.
Passo 2
Belezoca, agora outro passo importante é relacionar o ângulo que determina a direção de com aquele formado pela linha central e a horizontal, assim como na figura:
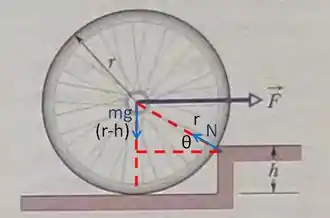
Temos todos os ingredientes agora para encontrarmos o valor de pedido na questão! Ela nos pede o menor valor de para que a roda consiga girar sobre o degrau. Isso só vai acontecer se o torque total exercido por essas forças (no sentido do vetor que entra no plano do papel) não for nulo, pois nesse caso a roda não está parada, em equilíbrio, mas está girando quando consegue ultrapassar o degrau, em relação ao eixo de contato:
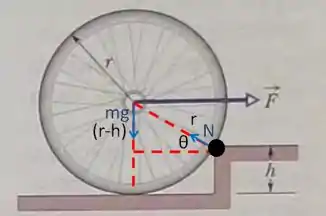
De forma que os torques serão medidos pelo raio perpendicular a esse ponto de contato, onde a roda irá girar.
Passo 3
Considerando a situação limite em que a roda consegue fazer a ultrapassagem, temos:
Onde o torque total será dado como:
De forma que os raios perpendiculares, serão dados como na figura:
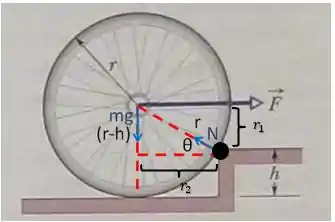
Sendo assim, temos que o torque será:
Passo 4
Vamos agora encontrar o valor de Com ele, conseguimos isolar na equação acima e encontrar a resposta. Para isso, vamos voltar a analisar a figura do passo 2:
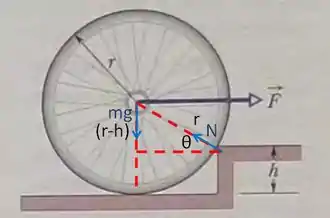
Lembrando que:
Sendo assim, temos que:
Passo 5
Belezera, agora podemos jogar o valor do acima na equação do passo 1:
Tal que:
Dividindo tudo por , temos que:
Logo:
Substituindo os valores do enunciado,temos:
Logo a força mínima deve ser igual a:
