Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.Problemas Adicionais - Ex. 83
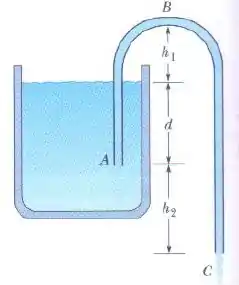
A figura mostra um sifão, que é um tubo usado para transferir líquidos de um recipiente para outro. O tubo deve estar inicialmente cheio, mas, se essa condição é satisfeita, o líquido escoa pelo tubo até que a superfície do líquido no recipiente esteja no mesmo nível que a extremidade do tubo. O líquido tem uma massa específica de e viscosidade desprezível. As distâncias mostradas na figura são , , e . (a) Com que velocidade o líquido sai do tudo no ponto ? (b) Se a pressão atmosférica é , qual é a pressão do líquido em , o ponto mais alto do tubo? (c) Teoricamente, até que altura máxima esse sifão pode fazer a água subir?
Passo 1
Show de bolinhas galerinha do RespondeAí, tudo beleza?
Nesse exercício aqui, temos um sifão, que deveria estar inicialmente cheio, mas se essa condição fosse satisfeita, o liquido deveria escoar pelo tubo até que a superfície do liquido o recipiente onde o sifão está contido, ficasse no mesmo nível que a extremidade do sifão.
Sabendo que o liquido possui densidade e as alturas são , e , na letra (a), o enunciado pede pra gente encontrar com que velocidade o liquido sai do tubo no ponto .
Iradosom então como queremos encontrar a velocidade de um fluido, quando temos a pressão e a altura, podemos pensar logo na equação de Bernoulli, dada como:
Agora, essa equação comparar dois pontos do sistema, a grande questão é escolher quais pontos nós vamos comparar. Bora lá.
Passo 2
Belezoca, então o ponto vai ser um dos pontos em que vamos aplicar a equação. E o outro? Vamos escolher um que seja mais simples.
Vamos chamar de um ponto na superfície do recipiente onde ele estaria sujeito apenas à pressão atmosférica, tem velocidade nula e altura conhecida em relação ao ponto .
Aplicando a equação de Bernoulli:
Como o ponto também tem uma abertura para o exterior, a pressão sobre ele também é a pressão atmosférica, portanto:
Assim:
Arrumando um pouquinho:
Como o ponto está na superfície do recipiente, teremos que a variação de altura entre e vai ser dada como:
E como , obtemos:
Isolando a velocidade :
Substituindo os valores:
Passo 3
(b) Agora queremos saber qual é a pressão no ponto , que fica no topo do tubo em U.
E vamos aplicar a equação de Bernoulli entre esse ponto e o ponto , já que nós já sabemos bastante sobre ele:
A pressão é o que queremos descobrir, e o ponto está aberto para a atmosfera.
Como os dois pontos estão no mesmo “tubo”, pela equação da continuidade:
E a equação de Bernoulli fica:
Arrumando os termos, teremos que:
Logo:
E essa é a resposta da letra (b).
Passo 4
A letra (c) é uma pergunta um pouco mais conceitual: até que altura máxima o sifão poderia fazer a água subir?
Conforme o topo do sifão fica mais alto, a pressão naquele ponto vai diminuindo. No limite, a pressão fica praticamente zero. Vamos ver em qual altura isso acontece.
Aproveitando a fórmula que tínhamos achado logo acima:
De modo que:
O que nos dá:
Isolando :
Então na situação extrema onde , teremos que a altura máxima será:
Logo:
Prontinho!
Resposta
(a)
(b)
(c)