Exercícios de Aplicações da Hidrodinâmica - Lista de Exercícios Resolvida
Questão 1
Uma torneira aberta deixa vazar água continuamente em regime permanente. Considere que a água é um fluido incompressível.
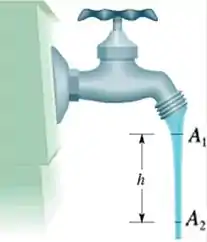
Nota-se que o filete de água vai se estreitando. Por que isso acontece?
Ver solução completaQuestão 2
O tubo horizontal mostrado na figura apresenta seção reta com área igual a em sua parte mais larga e em sua constrição. A água flui no tubo, e vazão volumétrica é igual a (, Calcule:
- A velocidade do escoamento na parte mais larga e na constrição.
- A diferença de pressão entre essas duas partes.
- A diferença de altura entre os dois níveis de mercúrio existente no tubo em U.
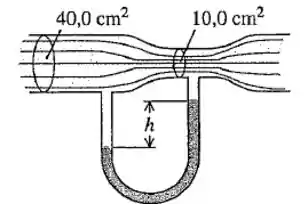
Dado:
Ver solução completaQuestão 3
Dois tanques abertos estão cheios de um mesmo fluido de densidade constante, como ilustrado na figura. Um tubo horizontal tem uma extremidade conectada ao fundo do primeiro tanque e outra extremidade aberta, de modo que o fluido pode escoar para fora do tanque. O tubo possui um estrangulamento () onde a área da seção reta é a metade da área nas extremidades ( e ). Conectamos com um tubo em U o estrangulamento ao segundo tanque, de modo que a extremidade do tubo fica imersa no fluido. Com isso uma coluna de fluido preenche o tubo até uma a altura , após atingido o equilíbrio. Considere que a densidade do ar entre os pontos e é suficientemente pequena para desprezarmos variações de pressão com a altura. Considere também que as áreas das superfícies de fluido nos dois tanques são muito maiores que as das seções retas do tubo horizontal, que o escoamento do fluido através do mesmo é estacionário e que a aceleração da gravidade e a pressão atmosférica são constantes e conhecidas em todos os pontos da figura.
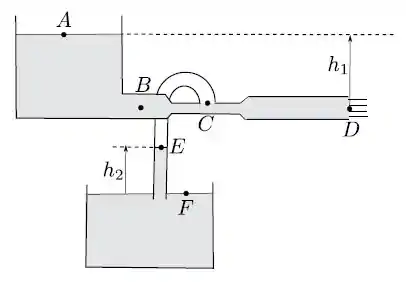
- Calcule a velocidade de escoamento do fluido no ponto indicado na figura.
- Calcule a velocidade do escoamento no ponto .
- Calcule a pressão manométrica (diferença entre a pressão absoluta e a pressão atmosférica) no ponto .
- Calcule a altura da coluna de fluido em termos da altura .
Questão 4
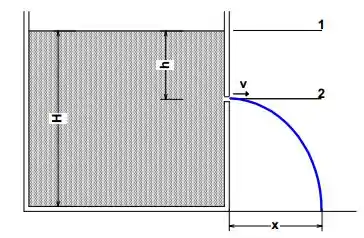
Um tanque contém água até uma altura . É feito um pequeno orifício na sua parede à profundidade da superfície, conforme a figura.
Mostre que a distância da base da parede até onde o jato atinge o solo é dada por .
Calcule a profundidade do buraco para que o jato emergente atinja o solo a uma distância máxima da base do tanque.
Questão 5
Água escoa em regime permanente no Venturi da figura. No trecho considerado, supõem-se as perdas por atrito desprezíveis e as propriedades uniformes nas seções. A área (1) é , enquanto a da garganta (2) é . Um manômetro, cujo fluido manométrico é mercúrio, é ligado entre as seções (1) e (2) e indica o desnível mostrado na figura. Pede-se a vazão da água que escoa pelo Venturi.
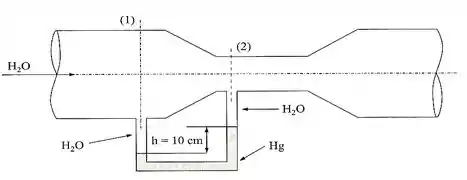
Considere
Ver solução completaQuestão 6
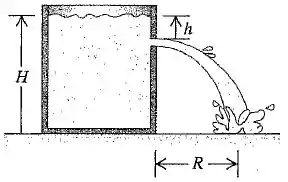
A água de uma grande tanque aberto com paredes verticais possui uma profundidade ( figura abaixo). Um orifício é aberto na parede vertical a uma profundidade abaixo da superfície da água.
- Qual é a distância entre a base do tanque e o ponto onde a corrente atinge o solo?
- Qual a distância acima da base do tanque devemos fazer um segundo furo para que a corrente que emerge dele tenha um alcance que igual ao do primeiro furo?
Questão 7
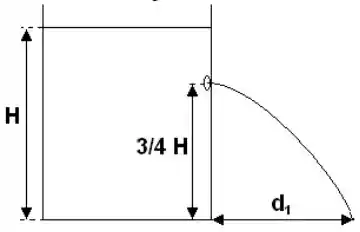
Considere um grande reservatório contendo um líquido de massa específica . Suponha que a altura do líquido seja e que é feito um furo pequeno no reservatório a da altura , conforme mostra a figura. Saindo pelo orifício, o líquido atinge uma distância da base do reservatório.
a) Calcule essa distância .
b) Calcule a altura de um segundo furo feito abaixo do primeiro e tal que o alcance do líquido saindo dele seja igual ao do primeiro. Para os seus cálculos, suponha que o nível do reservatório não se altera durante todo o processo.
Questão 8
Um sifão é usado para retirar líquido de um reservatório através de um tubo recurvado e fazendo jorrar água () em , como mostra a figura. A área do reservatório é muito maior do que a área da secção transversal do tubo; considere o fluido ideal e use e ,
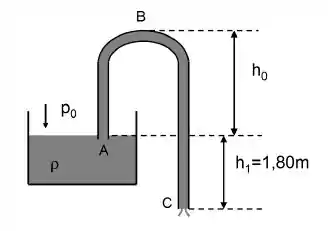
- Calcule a velocidade de escoamento em .
- Qual é o valor máximo de para o qual o sifão ainda funciona?
Questão 9
A figura abaixo mostra um garrafão de água mineral, hermeticamente fechado, que se encontra cheio até uma altura acima da boca da torneira. A área da boca da torneira é de (), muito menor do que a área da superfície da água dentro do garrafão. O ar acima da superfície da água está a uma pressão menor do que a pressão atmosférica, pressão manométrica . Considere o escoamento ideal, a aceleração da gravidade e .

- Determine a velocidade com que o fluido escoa.
- Calcule a vazão da torneira e determine o tempo necessário para se encher um copo de (volume igual a ).
- Ao sair da torneira, o jato de água fica mais fino durante a queda. Determine a área do jato após cair de uma altura abaixo da boca da torneira.
Questão 10
A água sai de uma torneira aberta de forma a formar um feixe que se afina, sem se dividir, conforme a água flui em direção ao ralo, como indica a figura. Supondo que a seção transversal deste feixe se mantém circular no decorrer do fluxo, com raio e velocidade da água imediatamente após sair da torneira, e considerando a água um fluido incompressível sem viscosidade (considere a aceleração da gravidade conhecida), estime:
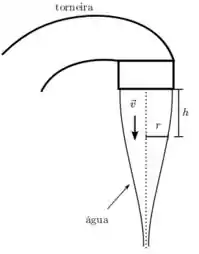
- A velocidade do fluido , em função da diferença de altura a partir da torneira.
- O raio de seção transversal do feixe, em função do módulo de velocidade nesta seção do fluido.
- O raio de uma seção transversal de um feixe, , agora em função da diferença de altura a partir da torneira.
Questão 11
A figura mostra um sifão, que é um tubo usado para transferir líquidos de um recipiente para outro. O tubo deve estar inicialmente cheio, e se esta condição é satisfeita o líquido escoa pelo tubo até que a superfície do líquido no recipiente esteja no mesmo nível que a extremidade . O líquido tem densidade igual a e viscosidade desprezível. As distâncias mostradas na figura são , e . Considere .
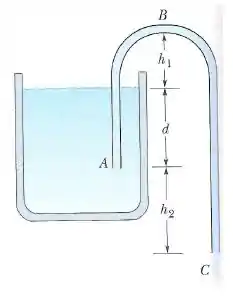
- Com que velocidade o líquido sai do tubo no ponto ?
- Se a pressão atmosférica é , qual é a pressão do líquido no ponto , o ponto mais alto do tubo?
- Qual é o máximo valor de , mantidos e , para que o líquido continue escoando?
Questão 12
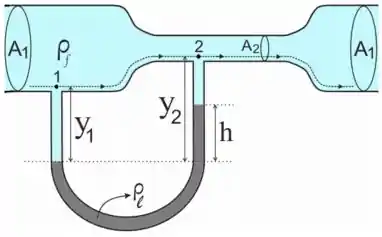
O medidor de Venturi é usado para se obter a velocidade de escoamento estacionário de um fluido não viscoso em uma tubulação. Considere um fluido incompressível, de densidade , que escoa em uma tubulação com área ade seção transversal Na região de estrangulamento, a área é reduzida pra , e um tubo manométrico é instalado como mostrado abaixo (vide figura). Suponha que o liquido do manômetro também seja incompressível e tenha densidade . NÃO despreze termos como
- Obtenha a diferença de pressão entre os pontos 1 e 2 em termos dos dados e da velocidade no ponto 1
- Determine a altura lida no medidor em função da diferença de pressão entre os pontos 1 e 2.
- Determine a velocidade de escoamento em termos dos dados do problema e das respostas anteriores.
Questão 13
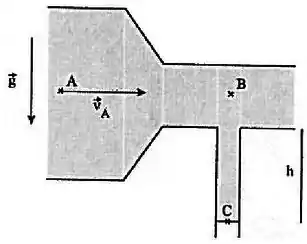
Considere o encanamento abaixo, por onde corre horizontalmente, em regime estacionário, um fluido não viscoso de densidade . A extremidade do cano vertical está aberta para a atmosfera e a coluna de líquido nele contida não cai.
Considere conhecidas a pressão , a seção reta e a velocidade no ponto , a altura do cano vertical, a gravidade e a pressão atmosférica .
- Quais a velocidade e a pressão do fluido no ponto em função da seção reta no ponto ?
- Discuta o sinal de a partir das expressões obtidas no item anterior.
- Qual o valor de para que a coluna vertical de líquido não caia?
Questão 14
A figura abaixo mostra um garrafão de água mineral, hermeticamente fechado, que se encontra cheio até uma altura acima da boca da torneira. A área da boca da torneira é de (), muito menor do que a área da superfície da água dentro do garrafão. O ar acima da superfície da água está a uma pressão menor do que a pressão atmosférica, pressão manométrica . Considere o escoamento ideal, a aceleração da gravidade e .

- Determine a velocidade com que o fluido escoa.
- Calcule a vazão da torneira e determine o tempo necessário para se encher um copo de (volume igual a ).
- Ao sair da torneira, o jato de água fica mais fino durante a queda. Determine a área do jato após cair de uma altura abaixo da boca da torneira.
Questão 15
II. A figura abaixo mostra um medidor Venturi, usado para medir a velocidade de um fluido num cano. Ele consiste de um segmento de cano de diâmetro com um estreitamento de diâmetro e um manômetro que mede a diferença de pressão entre a parte mais larga e mais estreita. Aplicando a equação da continuidade e a Equação de Bernoulli aos pontos 1 e 2,
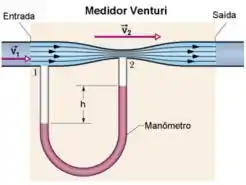
b) encontre a expressão da velocidade em função dos diâmetros , da massa específica do fluido e da diferença de pressão ().
c) Suponha que o fluido seja água doce, que o diâmetro do cano seja e o do estreitamento , e que a diferença de pressão seja . Calcule a vazão de água em e em ?
Ver solução completaQuestão 16
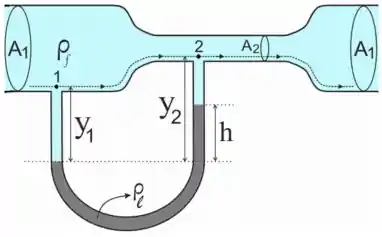
O medidor de Venturi é usado para se obter a velocidade de escoamento estacionário de um fluido não viscoso em uma tubulação. Considere um fluido incompressível, de densidade , que escoa em uma tubulação com área ade seção transversal Na região de estrangulamento, a área é reduzida pra , e um tubo manométrico é instalado como mostrado abaixo (vide figura). Suponha que o liquido do manômetro também seja incompressível e tenha densidade . NÃO despreze termos como
- Obtenha a diferença de pressão entre os pontos 1 e 2 em termos dos dados e da velocidade no ponto 1
- Determine a altura lida no medidor em função da diferença de pressão entre os pontos 1 e 2.
- Determine a velocidade de escoamento em termos dos dados do problema e das respostas anteriores.
Questão 17
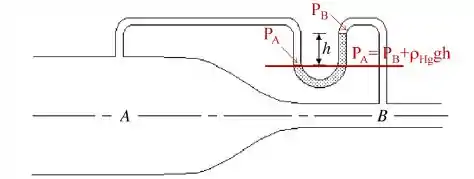
Água escorre por um cano horizontal de calibre variável, como mostrado na Figura. No ponto A, a área de secção transversal é de 25,0 cm² e a velocidade da água é de 2,00 m/s. Em B, a área é de 16,0 cm². O fluido no manômetro é mercúrio cuja desidade é de kg/m³. Trate a água como fluido ideal com densidade de 1000 kg/m³. Despreze a variação da pressão ao longo da seção transversal do cano. Qual é a leitura do manômetro?
- 0,546 cm
- 1,31 cm
- 2,81 cm
- 2,12 cm
- 3,36 cm
Questão 18
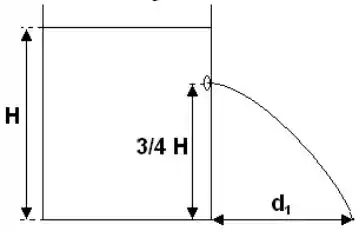
Considere um grande reservatório contendo um líquido de massa específica . Suponha que a altura do líquido seja e que é feito um furo pequeno no reservatório a da altura , conforme mostra a figura. Saindo pelo orifício, o líquido atinge uma distância da base do reservatório.
a): Calcule essa distância .
b): Calcule a altura de um segundo furo feito abaixo do primeiro e tal que o alcance do líquido saindo dele seja igual ao do primeiro. Para os seus cálculos, suponha que o nível do reservatório não se altera durante todo o processo.
Questão 19
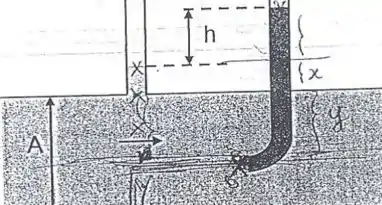
Quando um tubo retilíneo e outro com um cotovelo são acoplados a uma tubulação onde flui uma correnteza horizontal de água com velocidade , o nível da água no interior dos tubos começa a subir até que a pressão externa seja suficiente para estagnar o fluxo de água dentro dos tubos acoplados. Nesta situação, a diferença entre os níveis de água nos dois tubos verticais é , como ilustrado na figura. Considere um fluido ideal e
- Calcule a velocidade da correnteza.
- Considere que a área transversal, , é reduzida pela metade e a vazão mantida. Nesta situação, qual o novo valor de
Questão 20
A figura mostra um sifão, que é um tubo usado para transferir líquidos de um recipiente para outro. O tubo deve estar inicialmente cheio, e se esta condição é satisfeita o líquido escoa pelo tubo até que a superfície do líquido no recipiente esteja no mesmo nível que a extremidade . O líquido tem densidade igual a e viscosidade desprezível. As distâncias mostradas na figura são , e . Considere .
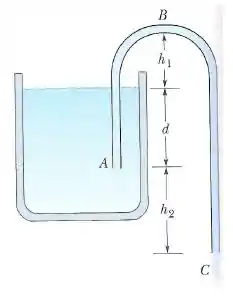
- Com que velocidade o líquido sai do tubo no ponto ?
- Se a pressão atmosférica é , qual é a pressão do líquido no ponto , o ponto mais alto do tubo?
- Qual é o máximo valor de , mantidos e , para que o líquido continue escoando?
Questão 21
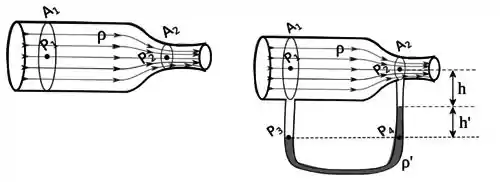
A figura abaixo mostra um trecho de um tubo de paredes rígidas por onde escoa um fluido incompressível, de densidade ρ, em regime estacionário. Despreze os efeitos da viscosidade do fluido. Seja a área da seção reta da parte esquerda do tubo e a área da seção reta da parte direita. A velocidade do fluido no ponto é 1. Considere conhecida a aceleração da gravidade. Responda:
- Qual a velocidade do fluido 2 no ponto P2? Escreva sua resposta em termos de 1, e .
- b) Qual a diferença () das pressões do fluido, respectivamente, nos pontos P2 e P1? Escreva sua resposta em termos de 1, ρ, A1 e A2 .
- Encontre a pressão p3 no ponto P3 em função de p1 e a pressão p4 em P4 em função de p2 . Escreva suas respostas também em termos de ρ, ρ′ e ′.
- Reobtenha a diferença () das pressões do fluido, respectivamente nos pontos P2 e P1, mas agora em termos de ρ, ρ′ e ′.
- Determine a velocidade 1, em termos de ρ, ρ′ , ′ , A1 e A2. Considere a área da seção reta do tubo em desprezível quando comparada com A1 e A2 .
- Qual deve ser o valor de ′ para que as pressões nos pontos P1 e P2 sejam iguais? O que acontece com o escoamento do fluido de densidade ρ neste caso?
É acoplado neste tudo, um pequeno tubo em (a figura está fora de escala), como indica a figura abaixo à direita, preenchido por um fluido também ideal e incompressível de densidade ρ′ a fim de que, medindo a altura ′ de desnível entre os dois braços deste tubo, seja possível encontrar a velocidade . A altura dos pontos P1 e P2 em relação ao desnível do fluido de densidade ρ′ é .
Questão 22
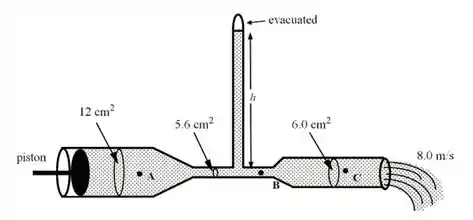
Um tubo de vidro tem três secções com áreas diferentes, cujos valores estão indicados na figura abaixo. Um pistão exerce uma força no lado esquerdo do tubo que faz o mercúrio dentro do tubo fluir, saindo do lado direito a uma velocidade de . Três pontos dentro do tubo estão indicados pelas letras A, e . Note que não é desenhado na escala correta e a densidade do mercúrio é Qual a pressão total no ponto ?
Questão 23
Sobre os pontos 1, 2 e 3 (à mesma altura) representados na figura, marque a única alternativa correta:
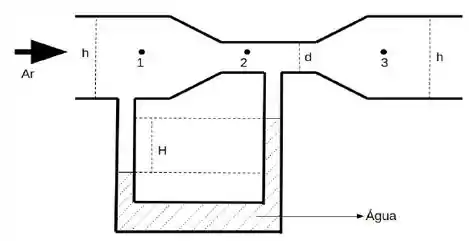
- As pressões nesses pontos são iguais, assim como as velocidades.
- As pressões nos pontos 1 e 3 são iguais entre si e menores que a pressão no ponto 2. As velocidades nos pontos 1 e 3 são iguais entre si e maiores que a velocidade no ponto 2.
- As pressões nos pontos 2 e 3 são iguais entre si e menores que a pressão no ponto 1. As velocidades nos pontos 2 e 3 são iguais entre si e maiores que a velocidade no ponto 1.
- As pressões nos pontos 1 e 3 são iguais entre si e maiores que a pressão no ponto 2. As velocidades nos pontos 1 e 3 são iguais entre si e menores que a velocidade no ponto 2.
- As pressões nos pontos 1 e 3 são iguais entre si e maiores que a pressão no ponto 2. As velocidades nos pontos 1 e 3 são iguais entre si e maiores que a velocidade no ponto 2.
Questão 24
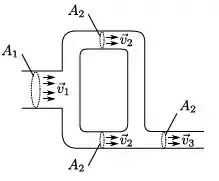
Consideremos um fluido incompressível realizando um escoamento estacionário como mostrado
na figura. Escreva a velocidade do fluido em função de e .
Questão 25
(a) A água de um porão inundado é bombeada verticalmente com uma velocidade através de uma mangueira com seção transversal de área . A mangueira passa por uma janela acima do nível da água e segue horizontalmente pelo jardim, onde também está a bomba. Qual é a potência da bomba em watts? (Sugestão: Uma porção do fluido de massa tem energias cinética e potencial. O trabalho da bomba deve ser igual à soma das duas no mesmo intervalo de tempo ).
(b) A mangueira e a bomba estão conectadas por um tubo de seção. Em , qual é o módulo da diferença de pressão na água ao passar da mangueira para o tubo de conexão com a bomba?
Dados:
Ver solução completaQuestão 26
Um tanque de água encontra-se sobre um carrinho que pode mover-se sobre um trilho horizontal com atrito desprezível. Há um pequeno orifício numa parede a uma profundidade abaixo do nível da água no tanque. A aérea do orifício é , a massa inicial da água é e a massa do carinho e do tanque é . Considerar . A densidade da água é .
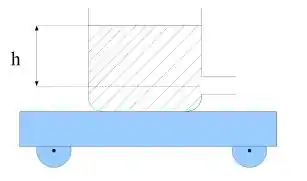
a) Qual é a velocidade inicial da água saindo do tanque?
b) Qual é a vazão da água na saída do tanque?
c) No tempo inicial, a velocidade do carrinho é nula. Durante um intervalo de tempo , uma massa de água é ejetada. Qual é a variação de velocidade do carrinho durante ? Escrever o resultado em função de e da velocidade relativa da água ejetada em relação ao carrinho.
d) Qual é o valor da aceleração inicial do carrinho?
Ver solução completaQuestão 27
A densidade da água é , e a altura da coluna de óleo . A densidade do óleo no lado esquerdo do tubo em mostrado na figura é:
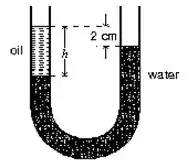
Questão 28
Se uma prensa for acionada com uma força de na área de , qual a força que será aplicada ao objeto na área com
Questão 29
Uma pessoa sopra horizontalmente acima de um dos lados de um tubo em forma de U, que contém água. O nível da água nesse lado do tubo:
- sobe ligeiramente.
- sobe se a pessoa não soprar com força e desce se a pessoa soprar com força.
- sobe se a pessoa soprar com força e desce se a pessoa não soprar com força.
- permanece o mesmo.
- desce ligeiramente.
Questão 30
Um tubo horizontal tem seção reta na parte mais larga e seção reta na parte mais estreita. O tubo possui um pistão que quando pressionado, aplica, ao atingir o regime estacionário, uma pressão e uma velocidade ao ar na parte larga do tubo. A parte estreita do tubo está conectada por um canudo vertical a um recipiente aberto contendo água. A distância vertical entre o tubo horizontal e a superfície livre da água é . Considere conhecidas as densidades do ar e da água , a aceleração da gravidade local e a pressão atmosférica . Faça a aproximação de que o ar seja incompressível.
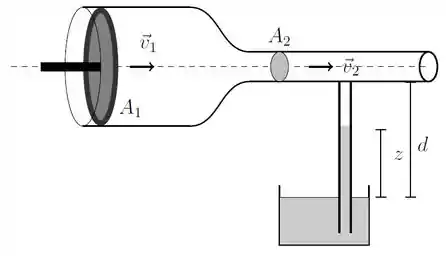
a) Determine a pressão na parte estreita em função da pressão e da velocidade na parte larga do tubo e da razão entre as seções retas.
b) Determine a altura da coluna de água no canudo vertical.
c) Determine a razão necessária para que a água seja aspirada através do canudo, entrando no tubo horizontal.
Ver solução completaQuestão 31
Na figura está representado um grande reservatório de água de altura , com uma tubulação horizontal de raio acoplada na lateral . Esta tubulação muda para uma tubulação vertical de menor raio na saída 2, , onde a água escoa para a atmosfera. Na figura
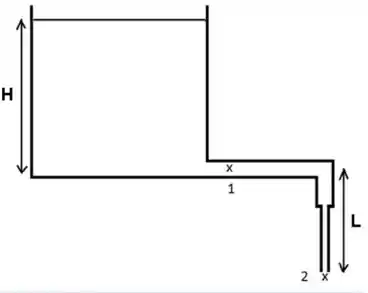
- Determine a altura para que a velocidade na saída 2da tubulação seja de
- Calcule a diferença de pressão entre as saídas 1 e 2 da figura, .(Valem os valores do item a).
- Quando a água escoa pra atmosfera no ponto 2, observa-se que o diâmetro do filete de água diminui enquanto cai. Calcule a distância que a água deve cai pra que o raio diminuía de ( na saída 2) para .( Valem os valores do item a).
Questão 32
Um grande tanque aberto superiormente, com paredes verticais, contém um fluido ideal em repouso com profundidade . Um orifício, com dimensões muito menores que as do tanque, é aberto em uma das paredes verticais na profundidade , pelo qual o fluido escoa com velocidade na direção horizontal. Determine a distância horizontal percorrida pelo jato de corrente após sair do tanque até tocar na base de apoio do mesmo. Considere a velocidade do fluido na superfície superior do tanque desprezível.
- .
- 2h
- 2
- 2(H – h)
- 2
Questão 33
A figura abaixo mostra um jorro de água saindo por um furo a uma distância h da superfície de tanque cuja altura da água é H.
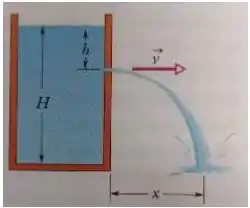
a) Calcule a que distância x que a água atinge o solo em termos de h e H.
b) A que profundidade deve ser feito um segundo furo para dar o mesmo valor de x?
c) Calcule a profundidade para a qual a distância que a água atinge o solo é máxima.
Ver solução completaQuestão 34
O ar flui através do tubo da figura abaixo com uma vazão de . Suponha que o ar seja um fluido ideal com densidade de enquanto mercúrio apresenta densidade de .
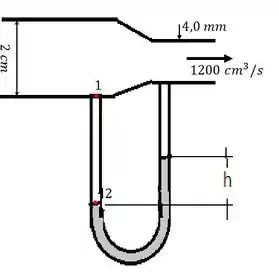
Desenhe as linhas de fluxo na figura.
A pressão no ponto é maior, igual ou menor que no ponto ? E em pontos correspondentes de mesma altura no ramo do lado direito? Justifique.
Qual é a altura de mercúrio no ramo direito do tubo em Se usar a equação de Bernoulli, deixe explicito em que pontos você a está aplicando.
Ver solução completaQuestão 35
Um reservatório A com superfície fechada, é conectado a um tubo B, aberto para a atmosfera, com área de seção reta constante e muito menor que a superfície de água em A, como mostra a figura.
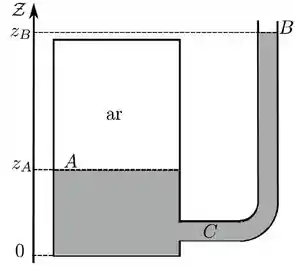
Considerando que existe um fluxo de água entre esses dois reservatórios, a velocidade da água no ponto C, indicado na figura, é dada por:
Escolha uma:
Questão 36
A figura mostra quatro recipientes preenchidos com o mesmo fluido incompressível, todos com um furo através do qual o fluido pode escoar. Todos são idênticos, mas o quarto tem um tubo conectado ao furo.
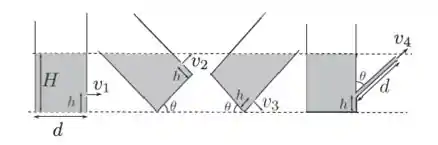
Considerando que a área da superfície livre do fluido é muito maior que a área do furo em todas as situações, e que todos os ângulos indicados são iguais a , marque a opção que indica a ordem correta do módulo da velocidade nos quatro casos.
(a) .
(b)
(c)
(d) .
(e)
Ver solução completaQuestão 37
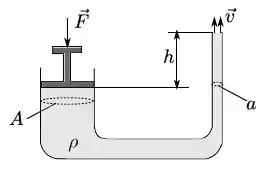
Um chafariz é feito usando-se um tubo em preenchido com um líquido de densidade , conforme figura. Do lado esquerdo a área da seção transversal do tubo é e do lado direito a área da seção transversal do tubo é . A saída do chafariz, do lado direito, está a uma altura do êmbolo e tem área igual ao tubo. Suponha que e que a pressão atmosférica seja . Qual o valor da força externaque se deve aplicar sobre o êmbolo para que o líquido saia do chafariz com uma velocidade
?
Questão 38
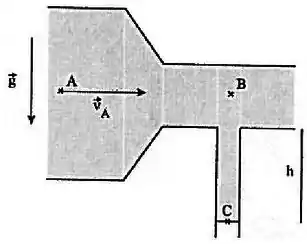
Considere o encanamento abaixo, por onde corre horizontalmente, em regime estacionário, um fluido não viscoso de densidade . A extremidade do cano vertical está aberta para a atmosfera e a coluna de líquido nele contida não cai.
Considere conhecidas a pressão , a seção reta e a velocidade no ponto , a altura do cano vertical, a gravidade e a pressão atmosférica .
- Quais a velocidade e a pressão do fluido no ponto em função da seção reta no ponto ?
- Discuta o sinal de a partir das expressões obtidas no item anterior.
- Qual o valor de para que a coluna vertical de líquido não caia?
Questão 39
O abastecimento de água em um edifício é realizado através de um cano principal com 4 cm de diâmetro. Nota-se que uma torneira com 2 cm de diâmetro, localizada a 2 m acima do nível de um trecho horizontal do cano principal, enche um recipiente de 9 litros em 30 segundos.
Use . A densidade da água é .
a) Calcule a velocidade com que a água deixa a torneira.
b) Calcule a pressão manométrica no cano principal de 4 cm de diâmetro.
Ver solução completaQuestão 40
Um orifício de de diâmetro encontrase abaixo da superfície do tanque de água de de diâmetro. Qual a vazão de volume através do orifício, em ?
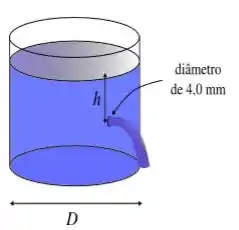
Ver solução completa
Questão 41
O que se pode dizer sobre um líquido em um recipiente que é rotacionado?
Escolha uma:
a. Ele se acumula próximo às bordas pois há uma força resultante que aponta do centro para as bordas nas partículas do líquido.
b. Ele se acumula próximo às bordas pois as partículas estão submetidas a uma força resultante centrípeta, gerada por uma variação de pressão ao longo do eixo radial.
c. A pressão é menor quanto mais perto do centro, logo, deixa de haver uma variação de pressão ao longo do eixo vertical.
d. Não há formação de um gradiente de pressão diferente do presente quando o líquido não é rotacionado.
e. É formado uma variação de pressão ao longo do eixo radial de forma.
Ver solução completaQuestão 42
Um regador é formado por uma garrafa plástica, perfurada por 20 furos de área 2 mm2 cada um, á qual se liga uma mangueira de água como na figura. Quando abrimos a torneira, a água escapa pela garrafa de modo que todos os furos têm a mesma velocidade de saída da água, vs. Considere a garrafa como um cilindro de diâmetro 10 cm. Sabendo que um dos jatos é emitido na vertical e alcança altura máxima de 1,25 m, calcule:

a) A velocidade de saída da água, vs, e a vazão total do regador.
b) Considerando a velocidade da água dentro da garrafa como sendo pequena (aproximadamente zero), obtenha a pressão manométrica da água dentro da garrafa. Você pode considerar as dimensões da garrafa como pequenas e desprezá-las.
c) Suponha que a garrafa aguenta uma pressão manométrica máxima de 8 atm. Assim, se aumentamos continuamente a pressão na mangueira e,consequentemente, a velocidade de vazão da água pelos furos, calcule a vazão máxima de água pelo regador imediatamente antes dele estourar.
Ver solução completaQuestão 43
Um sifão é usado para retirar um fluido incompressível de um recipiente aberto, como mostra a figura. A área de seção reta A é constante ao longo do tubo e muito menor que a área da superfície livre do fluido no recipiente.
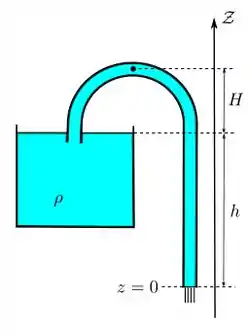
(a) Calcule a velocidade do fluido na saída do sifão, no regime estacionário.
(b) Calcule a pressão no ponto mais alto do sifão.
(c) Calcule o valor máximo da distância (H + h) para que o sifão funcione (o fluido saia na extremidade do tubo).
Ver solução completaQuestão 44
Dois tanques abertos estão cheios de um mesmo fluido de densidade constante, como ilustrado na figura. Um tubo horizontal tem uma extremidade conectada ao fundo do primeiro tanque e outra extremidade aberta, de modo que o fluido pode escoar para fora do tanque. O tubo possui um estrangulamento () onde a área da seção reta é a metade da área nas extremidades ( e ). Conectamos com um tubo em U o estrangulamento ao segundo tanque, de modo que a extremidade do tubo fica imersa no fluido. Com isso uma coluna de fluido preenche o tubo até uma a altura , após atingido o equilíbrio. Considere que a densidade do ar entre os pontos e é suficientemente pequena para desprezarmos variações de pressão com a altura. Considere também que as áreas das superfícies de fluido nos dois tanques são muito maiores que as das seções retas do tubo horizontal, que o escoamento do fluido através do mesmo é estacionário e que a aceleração da gravidade e a pressão atmosférica são constantes e conhecidas em todos os pontos da figura.
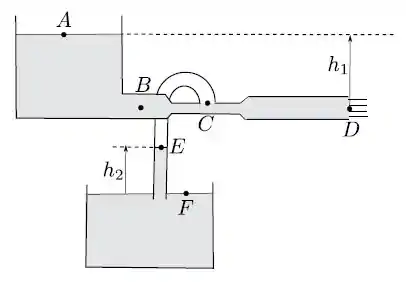
- Calcule a velocidade de escoamento do fluido no ponto indicado na figura.
- Calcule a velocidade do escoamento no ponto .
- Calcule a pressão manométrica (diferença entre a pressão absoluta e a pressão atmosférica) no ponto .
- Calcule a altura da coluna de fluido em termos da altura .
Questão 45
O tubo horizontal mostrado na figura abaixo tem uma seção transversal de área de na parte mais larga e na parte mais estreita, como indicado na figura. A água está escoando pelo tubo com uma vazão de . Esse tubo é conectado a outro tubo em formato U, contendo uma coluna de mercúrio. Ache:
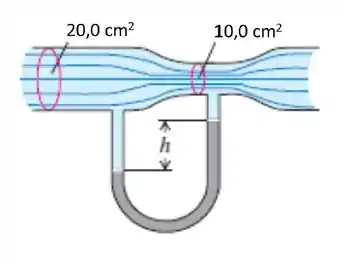
(a) A velocidade de escoamento na parte mais larga e na parte mais estreita .
(b) A diferença de pressão entre essas duas localizações considerando pontos de mesma altura.
(c) A diferença de altura entre as colunas de mercúrio no tubo em formato de U.
Dados:
Ver solução completaQuestão 46
Um sifão é usado para retirar líquido de um reservatório através de um tubo recurvado e fazendo jorrar água () em , como mostra a figura. A área do reservatório é muito maior do que a área da secção transversal do tubo; considere o fluido ideal e use e ,
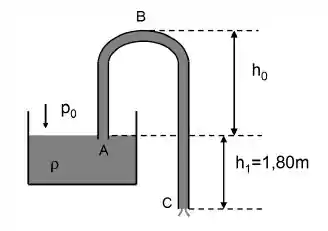
- Calcule a velocidade de escoamento em .
- Qual é o valor máximo de para o qual o sifão ainda funciona?
Questão 47
A figura mostra um sifão, que é um tubo usado para transferir líquidos de um recipiente para outro. O tubo ABC deve estar inicialmente cheio e nesta condição o líquido escoa pelo tubo até que a superfície do líquido no recipiente esteja no mesmo nível que a extremidade A do tubo. O líquido tem uma massa específica de 1000 kg/m³ e viscosidade desprezível. As distâncias mostradas na figura são h1= 25 cm e h2= 45 cm. Considere a área da seção reta do sifão constante.
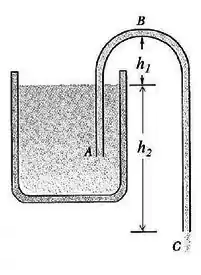
a)Determine o módulo da velocidade do líquido no ponto C.
b)Se a pressão atmosférica é 1x105Pa, qual é a pressão do líquido em B, o ponto mais alto do tubo?
c)Teoricamente, até que altura máxima h1esse sifão pode fazer a água subir?
Ver solução completaQuestão 48
Um sifão é um aparelho utilizado para remover líquido de um recipiente. Seu funcionamento é mostrado na figura ao lado. O tubo precisa estar inicialmente cheio e, a partir daí, o líquido fluirá através do tubo até que o nível do líquido no recipiente esteja abaixo da abertura . O líquido tem densidade ρ, viscosidade desprezível e a pressão atmosférica é . O volume do recipiente é muito maior que o do tubo. Baseado nessas informações escolha a alternativa correta.
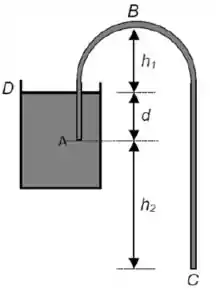
a) A velocidade do líquido em é menor que a velocidade em
b) A velocidade com que o líquido sai do tubo em é
c) A pressão em é maior que a pressão em
d) A pressão em é nula
e) A pressão em
Ver solução completa