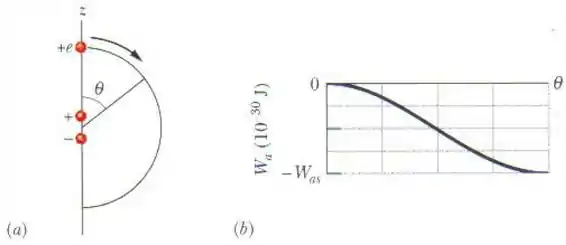
Na figura (a), uma partícula de carga +e está inicialmente no ponto z = 20 nm do eixo de um dipolo elétrico, do lado positivo do dipolo. (A origem do eixo zé o centro do dipolo.) A partícula é deslocada em uma trajetória circular em tomo do centro do dipolo até a coordenada z = -20 nm. A figura (b) mostra o trabalho realizado pela força responsável pelo deslocamento da partícula em função do ângulo que define a localização da partícula. A escala do eixo vertical é definida por . Qual é o módulo do momento do dipolo?
Passo 1
Como vamos relacionar o trabalho com o momento de dipolo? Te mostro. Vamos começar com esta equação:
Sabemos que . Mas e ? Temos como saber? Tem alguma fórmula relacionando potencial elétrico com dipolo? Tem!
Passo 2
Agora podemos achar ! Se liga, só:
Mas sabemos que :
Agora a gente joga isso lá naquela primeira equação:
E agora isola o p:
Passo 3
Agora, pela figura (b), nós sabemos o valor de W quando . Então é só substituir: