Exercícios de Potencial Elétrico Gerado por Carga Pontual - Lista de Exercícios Resolvida
Questão 1
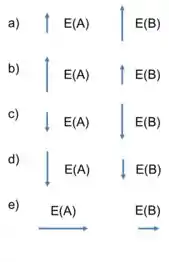
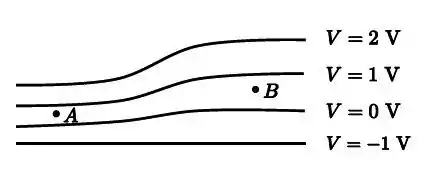
Considere o seguinte corte perpendicular a uma família de quatro superfícies equipotenciais, associadas a um campo eletrostático. Assinale a opção que melhor indica o vetor campo elétrico em cada um dos pontos A e B, respectivamente.
Questão 2
Uma carga positiva está localizada no ponto e e uma carga negativa está localizada no ponto e .
- Deduza uma relação para o potencial em qualquer ponto sobre o eixo em função da coordenada .
- Mostre que, quando , o potencial em qualquer ponto sobre a parte positiva do eixo é dado por
- Qual seria a resposta dos itens (b) e (c) se as cargas fossem trocadas de posição, ou seja, se fosse localizada em e em ?
Questão 3
Uma carga positiva está localizada no ponto e e uma carga negativa está localizada no ponto e .
- Faça um diagrama para mostrar as posições da cargas.
- Deduza uma relação para o potencial em qualquer ponto sobre o eixo em função da coordenada . Considere zero o potencial a uma distância infinita das cargas.
- Faça um gráfico do potencial sobre o eixo em função de de até .
- Qual seria a resposta do item (b) se as cargas fossem trocadas de posição, ou seja, se fosse localizada em e em ?
Questão 4
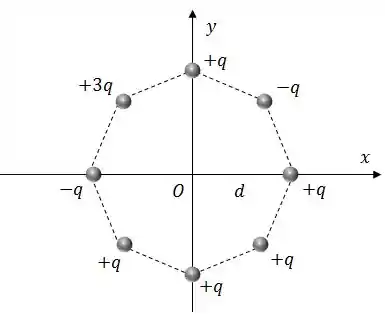
Calcule o campo elétrico no ponto devido à distribuição octogonal de cargas na figura (use o sistema de coordenadas indicado);
Calcule o potencial elétrico em ;
Qual será a aceleração instantânea adquirida por uma partícula de massa , carregada com uma carga positiva , abandonada em ?
Questão 5
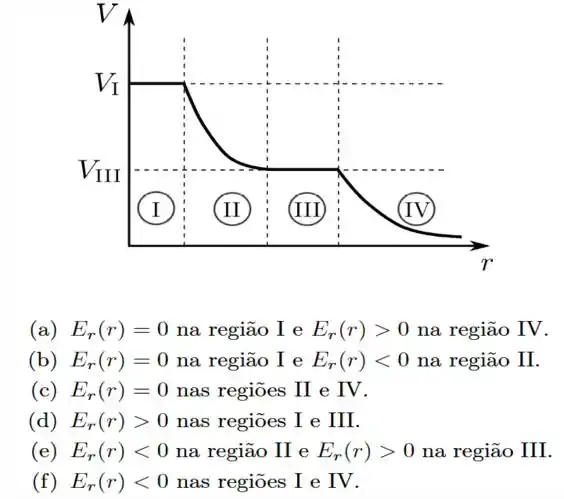
Uma certa distribuição estática de cargas produz um potencial eletrostático que depende apenas da distância até a origem de um sistema de coordenadas. O gráfico de é mostrado na figura abaixo, com quatro regiões destacadas. Sobre o campo eletrostático produzido por essa distribuição, , onde é o vetor unitário da direção radial, podemos afirmar que:
Questão 6
Sabendo que, na figura, e que o módulo de vale , responda:
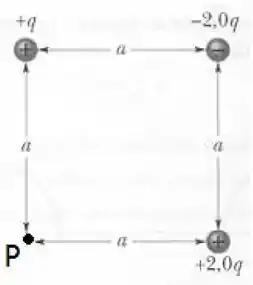
Qual é o valor do potencial elétrico no ponto ?
Qual é a variação energia potencial elétrica para trazermos uma carga de prova do infinito até o ponto ?
Ver solução completaQuestão 7
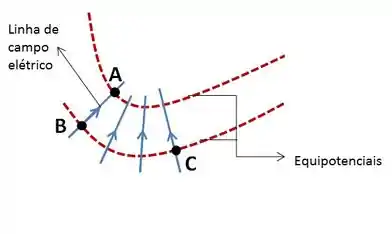
Na figura, quando um elétron se desloca de para ao longo de uma linha de campo elétrico, esse campo realiza um trabalho de . Quais são as diferenças de potencial elétrico:
(a)
(b)
(c)
Questão 8
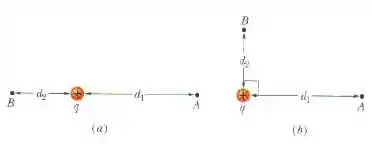
Considere uma carga pontual , o ponto a uma distância de e o ponto a uma distância de .
(a) Se e estão diametralmente opostos como na figura (a), qual é a diferença de potencial elétrico ?
(b) Qual é a diferença de potencial elétrico se e estão localizados como na figura (b)?
Questão 9
Um campo elétrico uniforme está orientado do oeste para o leste. O ponto está a oeste do ponto , o ponto está a leste do ponto e o ponto está ao sul de . Para cada ponto , e , determine se o potencial do ponto é maior, menor ou igual ao do ponto .
Ver solução completaQuestão 10
Marque como verdadeiro ou falso:
- Uma esfera não condutora de raio tem uma distribuição de carga uniforme no seu volume. Podemos afirmar que o valor do potencial eletrostático em um ponto na sua superfície depende da escolha da origem do potencial;
- Se o campo eletrostático é zero em toda uma região, então o potencial é constante em toda essa região;
- Se o módulo do vetor campo elétrico tiver o mesmo valor em todos os pontos da superfície de um condutor em equilíbrio eletrostático, então as cargas estão uniformemente distribuídas em sua superfície;
- Dado que a superfície de um condutor, em equilíbrio eletrostático, é equipotencial, então as cargas estão uniformemente distribuídas em sua superfície.
- Se num dado ponto o campo eletroestático é zero, então o potencial eletroestático também vale zero nesse ponto.
Questão 11
Considera as seguintes afirmativas:
- No interior de um condutor em equilíbrio eletrostático, o potencial é sempre nulo;
- Se o campo elétrico é nulo em um determinado ponto do espaço, o potencial elétrico também será nulo nesse ponto;
- Se o potencial elétrico é nulo em um determinado ponto do espaço, o campo elétrico também deve ser nulo nesse ponto.
Quais delas são verdadeiras?
- Apenas a I
- Apenas a II
- Apenas a III
- Apenas a I e a II
- Apenas a I e a III
- Apenas a II e a III
- Todas são verdadeiras
- Nenhuma é verdadeira
Questão 12
Duas esferas condutoras, carregadas, de raios e estão afastadas a uma distância muito grande, de modo que o campo elétrico na vizinhança de cada esfera pode ser considerado como somente devido à distribuição de carga uniforme da própria esfera. As esferas estão ligadas por um fio condutor fino que simplesmente promove o contato elétrico entre elas. Se , qual é a afirmação verdadeira?
Questão 13
A figura à seguir mostra esquematicamente uma seção transversal de um objeto condutor maciço (de carga elétrica total nula) colocado em um campo eletrostático externo, após atingido o equilíbrio eletrostático.
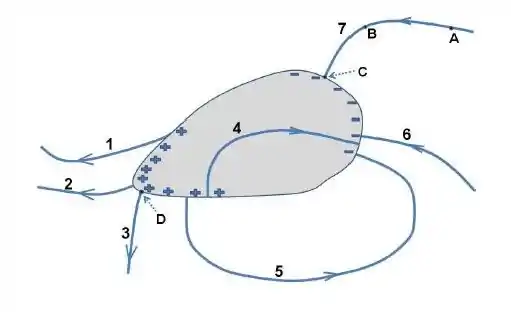
As letras , , e assinalam quatro diferentes pontos. Marque a opção que relaciona corretamente os potenciais eletrostáticos nos referidos pontos:
- e
- e
- e
- e
- e
- e
- e
Questão 14
Duas partículas (pontuais), separadas por uma distância , com cargas elétricas e diferentes (), produzem um potencial nulo num ponto do espaço. Tomando o potencial como zero no infinito, isso significa necessariamente que:
- Não há outra força elétrica atuando sobre uma outra partícula de teste colocada no ponto
- As cargas e devem ter o mesmo sinal
- O trabalho para colocar a partícula de carga a uma distância da partícula de carga é zero
- O trabalho para trazer uma partícula de teste carregada, desde o infinito até o ponto , é zero
Questão 15
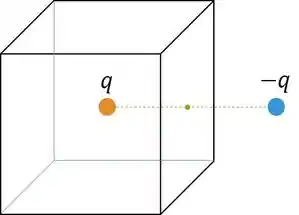
Na figura à seguir, temos duas partículas (pontuais), com carga e . Aquela de carga está envolvida por uma superfície (gaussiana) cúbica, com aresta de comprimento situando-se no centro do cubo. Um segmento de reta, também de comprimento , perpendicular a uma das faces do cubo, une as duas partículas. Para esse arranjo obteve-se: (I) o fluxo do vetor campo elétrico sobre toda a superfície gaussiana; (II) o fluxo do vetor campo elétrico sobre a face do cubo situada entre as cargas; (III) o potencial elétrico num dos vértices (ponto P) nessa mesma face. Os valores para essas grandezas são:
- , ,
- , ,
- , ,
- , ,
- , ,
- , ,
Questão 16
Duas partículas de cargas e , separadas pela distância , produzem um potencial no ponto .
Traz-se então uma terceira partícula do infinito até o ponto . Sabendo-se que o potencial gerado pelas 3 partículas é nulo no infinito, pode-se concluir que:
O campo elétrico gerado apenas por e deve ser zero em .
O trabalho total para aproximar as partículas de carga e do infinito até a distância é zero.
O trabalho realizado pela força elétrica ao trazer-se a terceira carga do infinito para o ponto é zero.
A força elétrica exercida por e sobre é zero.
A energia potencial desse sistema de 3 cargas é zero.
Ver solução completaQuestão 17
O potencial elétrico em uma região do espaço é dado por , onde é uma constante não nula.
Deduza uma expressão para o campo elétrico na região.
Deduza o trabalho realizado pela força elétrica sobre uma partícula de carga , quando esta é deslocada do ponto até o ponto .
Seja agora uma região esférica, centrada na origem, de raio . Qual a carga no interior dessa superfície?
Obs.: você pode achar útil escrever o campo em coordenadas esféricas.
Ver solução completaQuestão 18
Considere uma esfera sólida, de raio R, não condutora e de densidade volumétrica de carga dada por
Concêntrica a essa esfera, temos uma casca esférica, espessa e condutora, em equilíbrio eletrostático, de raio interno e raio externo , onde foi depositada uma carga .
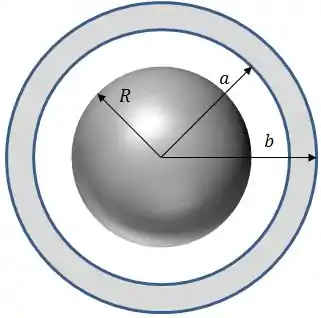
Calcule a carga total da esfera não-condutora.
Calcule o campo elétrico dentro da esfera não-condutora.
Calcule a densidade superficial de carga e nas superfícies interna e externa da casca, e expresse a sua resposta em termos de , , e .
Determine a diferença de potencial entre as superfícies da casca.
Ver solução completaQuestão 19
Três cargas pontuais se encontram nos vértices de um triângulo equilátero de lado . O centro do triângulo está na origem de um sistema de coordenadas cartesianas e o plano do triângulo fica no plano . Uma das cargas está no eixo as outras simetricamente nos quadrantes III e IV, como mostra a figura. A carga no eixo assim como a carga no quadrante IV tem o valor e a carga no quadrante IV tem o valor .
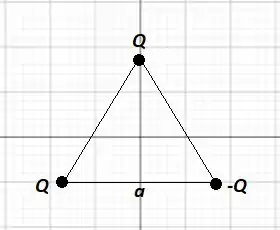
(b) Tomando o potencial elétrico no infinito como zero, calcule o potencial elétrico na origem.
Ver solução completaQuestão 20
Deseja-se acelerar um elétron do repouso até uma velocidade igual a da velocidade da luz. Sabendo que a massa do elétron vale , sua carga vale e a velocidade da luz vale , qual é a diferença de potencial a que ele deve ser submetido?
Questão 21
Dois semi-planos condutores infinitos se encontram num ângulo reto. Na região entre eles o potencial elétrico é dado por
onde é uma constante positiva.
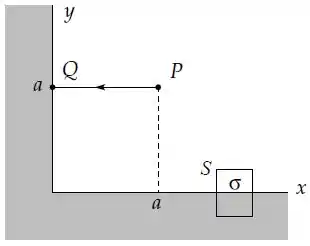
Determine o campo elétrico no primeiro quadrante .
Usando a lei de Gauss com a superfície fechada, cilíndrica e infinitesimal, mostrada de perfil na figura, determine a densidade superficial de carga na face horizontal do condutor.
Determine a integral de linha do campo elétrico
ao longo do segmento de reta , conforme a figura.
Ver solução completaQuestão 22
Uma camada semiesférica isolante de raio interno e externo tem uma densidade volumétrica de carga que decresce com o inverso da distância ao centro segundo .
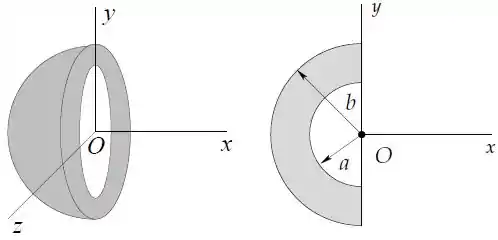
Dados e .
- Determine a carga total da camada semiesférica.
- Determine o potencial elétrico no ponto da cama semiesférica. Adote potencial nulo no infinito.
- Se uma carga pontual com o mesmo sinal da constante da densidade volumétrica de carga é solta no centro , qual é a velocidade final que ela atinge?
Questão 23
Considere que os terminais de uma bateria com uma DDP conhecida estão conectados a duas placas (planas) condutoras, muito grandes, e perpendiculares ao eixo . As placas não se tocam, e têm uma distribuição superficial de cargas uniforme e estacionária. Saiba ainda que a placa de menor (maior) potencial está localizada em . Um elétron com massa e carga é lançado na região interior às placas, com uma velocidade inicial . A evolução temporal das coordenadas e do elétron dentro da região limitada pelas placas pode ser dada por:
- ;
- ;
Questão 24
Quatro cargas puntiformes são colocadas nos vértices e de um retângulo, de
acordo com a figura abaixo. O retângulo tem lados de comprimento e . Considere
.
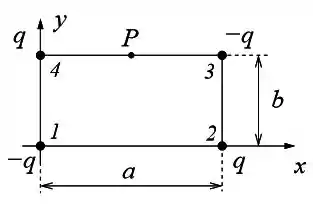
Calcule o vetor força resultante que atua na carga localizada na origem
(vértice ).
Determine o vetor campo elétrico no centro do retângulo ponto de
coordenadas .
Calcule o trabalho necessário para trazer uma carga do infinito até o
ponto de coordenadas .
Ver solução completaQuestão 25
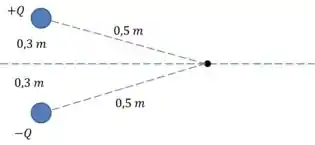
Duas cargas de sinais opostos e iguais magnitudes são mantidas a uma distância de entre si, como mostrado na figura. ()
I – Assinale a opção que representa a magnitude do campo elétrico no ponto P.
a)
b)
c)
d)
e) zero
II – Assinale a opção que representa o potencial elétrico no ponto P.
a)
b)
c)
d)
e) zero
Questão 26
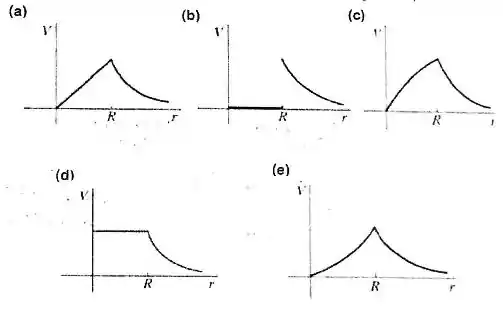
Uma casca esférica fina e oca de raio é carregada com um excesso de carga positiva. Qual dos gráficos ilustra corretamente o potencial elétrico devido à casca carregada em função da distância ao centro da casca. Considere a origem do potencial em .
Questão 27
![]()
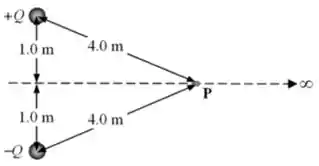
a) (0,5 pontos) Assinale a opção que representa o potencial elétrico no ponto .
a)
b)
c)
d)
e)
Ver solução completaQuestão 28
A esfera condutora de raio (Esfera 1) possui carga elétrica . Ela é conectada por meio de um fio a uma segunda esfera condutora neutra de raio (Esfera 2). A carga é distribuída entre as duas esferas e o equilíbrio eletrostático é estabelecido. e são as respectivas cargas das esferas após a conexão do fio.
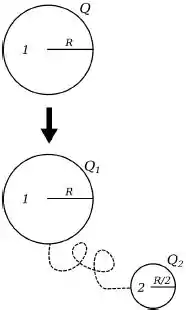
Qual a relação entre as cargas nas duas esferas?
Ver solução completa
Questão 29
Sejam duas partículas carregadas com cargas e , separadas por uma distância de .
O campo elétrico é nulo entre as cargas a uma distância de 2,5cm de .
O campo elétrico e o potencial são nulos no mesmo ponto, a uma distância de de entre as cargas.
Não existe um ponto em que o campo elétrico é nulo e o potencial é nulo a uma distância de de entre as cargas.
O potencial é nulo a uma distância de de entre as cargas.
O campo elétrico é nulo a uma distância de de e o potencial é nulo no mesmo ponto.
Ver solução completaQuestão 30
Três cargas pontuais de , , e são colocadas ao longo do eixo , como mostrado na figura.
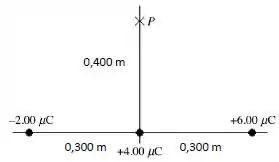
Qual é o potencial elétrico no ponto (em relação ao infinito), devido a essas cargas?
;
;
;
;
;
Ver solução completaQuestão 31
Suponhamos que uma região do espaço tem um campo eléctrico uniforme, dirigida para a direita, como mostrado na figura.
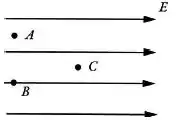
Qual afirmação sobre o potencial elétrico é verdadeira?
O potencial em todas as três posições é o mesmo porque o campo é uniforme.
O potencial nos pontos e são iguais, e o potencial no ponto é maior do que o potencial no ponto .
O potencial nos pontos e são iguais, e o potencial no ponto é menor do que o potencial no ponto .
O potencial no ponto é o mais elevado, o potencial no ponto é o segundo mais elevado, e o potencial no ponto é o mais baixo.
O potencial no ponto é o mais elevado, o potencial no ponto é o segundo mais elevado, e o potencial no ponto é o mais baixo.
Ver solução completaQuestão 32
O gráfico da figura mostra a variação do potencial eléctrico (em unidades arbitrárias) em função da posição (também em unidades arbitrárias).
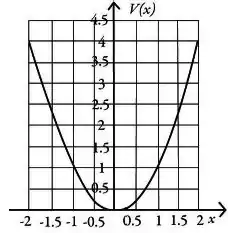
Qual das opções abaixo descreve corretamente a orientação da componente do campo elétrico ao longo do eixo ?
é positiva de até .
é positiva de até , e negativa de até .
é negativa de até , e positiva de até .
é negativa de até .
é zero de para .
Ver solução completaQuestão 33
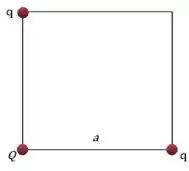
Três cargas pontuais ocupam vértices de um quadrado de lado , conforme a figura. Dois vértices opostos são ocupados por cargas iguais a e o terceiro é ocupado pela carga . Adote o infinito como referencial para potenciais nulos.
- Calcule em função de de modo que o potencial resultante no quarto vértice seja nulo.
- Considerando agora , calcule a energia potencial elétrica associada ao sistema de três cargas.
- Considerando sempre , calcule a variação de energia potencial elétrica ao movermos uma das cargas desde o vértice em que está até o quarto vértice do quadrado.
Questão 34
Considere o sistema abaixo, mantido fixo por forças externas, que consiste numa partícula pontual de carga e massa , situada na origem do sistema de coordenadas, e um semi-anel de raio situado no plano e centrado na origem. A densidade linear de carga do semi-anel depende do ângulo de acordo com a seguinte função: , onde é uma constante positiva.
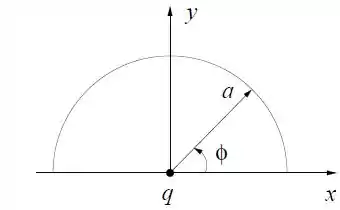
Calcule a carga total do anel;
Calcule o vetor força elétrica que age sobre a carga pontual;
Suponha que o anel é mantido fixo na sua posição e a partícula é liberada a partir do repouso. Qual será o módulo da velocidade da partícula quando ela se encontrar muito longe do anel?
Ver solução completaQuestão 35
13ª questão - Você fixa quatro cargas pontuais idênticas e de massa nos vértices de um quadrado de lado . Em seguida, você as libera simultaneamente, de modo que elas passam a se afastar. A máxima velocidade que cada carga atingirá será:
A) infinitamente grande
B)
C)
D)
E)
Ver solução completaQuestão 36
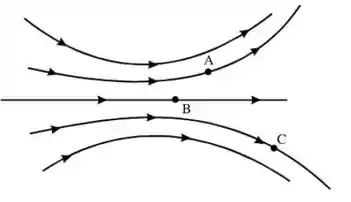
Suponhamos que uma região do espaço tem um campo elétrico não uniforme, dirigida para a direita, como mostrado na figura. Qual afirmação sobre o potencial elétrico é verdadeira?
Questão 37
Uma diferença de potencial é mantida entre duas grandes placas condutoras paralelas.
Um elétron parte do repouso sobre as superfícies de uma placa e acelera em direção à outra. Sua velocidade ao atingir a segunda placa é proporcional a:
;
;
;
;
;
Ver solução completaQuestão 38
Uma esfera de raio possui uma distribuição de carga não uniforme cuja densidade volumétrica é igual a , onde é uma constante positiva com dimensões: .
Calcule, utilizando explicitamente a Lei de Gauss:
O campo elétrico no ponto , a uma distância do centro da esfera.
O campo elétrico no ponto , a uma distância do centro da esfera.
A diferença de potencial entre os pontos e .
Suponha agora que uma carga puntiforme com massa e velocidade se desloque do infinito até o centro da esfera.
Calcule a distância mínima alcançada pela carga antes de ser repelida pela esfera.
(Sugestão: calcule o potencial da esfera numa distância genérica e utilize a conservação da energia).
Ver solução completaQuestão 39
Considere as seguintes afirmações:
- Em um ponto qualquer do interior de um condutor em equilíbrio eletrostático, o campo elétrico é sempre nulo;
- Em um ponto qualquer do interior de um isolante, o campo elétrico é sempre nulo;
- Se o fluxo do campo elétrico resultante através de uma superfície fechada (gaussiana) for zero, então não existem partículas carregadas no interior dessa superfície;
- Para todos os pontos (internos e na superfície) de um condutor em equilíbrio eletrostático o potencial é o mesmo.
Dessas afirmações, quais são todas as corretas?
- I, IV
- I
- III
- IV
- I, III, IV
Questão 40
O potencial elétrico de uma placa de vidro muito grande é . Ela tem uma distribuição de carga positiva e uniforme sobre sua superfície com uma densidade .
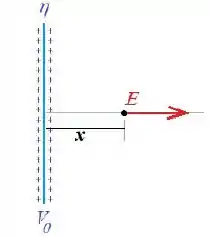
Determine o potencial a uma distância da placa. Considere que o ponto está longe das bordas e que é muito menor que as dimensões da placa.
Ver solução completa
Questão 41
Qual das seguintes afirmativas sobre condutores em equilíbrio eletrostático é verdadeira?
Para mover uma carga positiva sobre a superfície de um condutor é necessário a realização de trabalho positivo.
Independente do formato da superfície de um condutor, cargas colocadas sobre essa superfície irão se distribuir de forma uniforme.
O potencial elétrico no interior de um condutor é sempre nulo.
O volume e a superfície de um condutor têm o mesmo potencial.
O potencial elétrico na superfície de um condutor é sempre nulo.
Ver solução completaQuestão 42
Três partículas carregadas com cargas , e são fixadas sobre os vértices de um triângulo equilátero, como mostrado na figura abaixo. O centro do triângulo é indicado pelo ponto
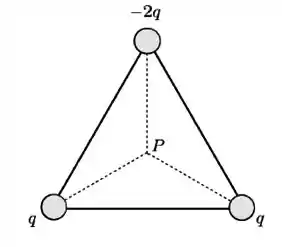
Considere que a energia potencial elétrica seja nula quando as cargas estiverem infinitamente afastadas. Sobre esse sistema, são feitas as afirmativas abaixo:
- A energia potencial elétrica do sistema é negativa.
- O potencial elétrico é constante sobre um eixo perpendicular ao triângulo e que passa por .
- O trabalho realizado pela força elétrica sobre uma partícula carregada, quando ela é deslocada do infinito até o ponto , é nulo.
São VERDADEIRAS as afirmativas:
- Nenhuma delas.
Questão 43
Duas partículas puntiformes carregadas com a mesma carga positiva, fixas sobre o eixo , estão localizadas simetricamente em relação à origem, uma em e a outra em .
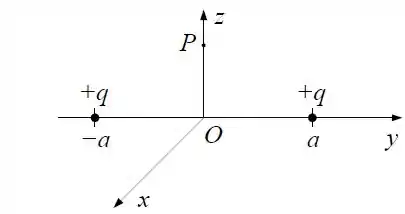
Determine o potencial eletrostático num ponto qualquer do espaço.
Suponha que uma partícula com carga seja abandonada do repouso no ponto com . Determine a energia cinética da carga quando ela passar pela origem do sistema de coordenadas (despreze a forca peso).
Calcule a energia potencial do sistema formado pelas três cargas na configuração em que a carga −Q está no ponto e na configuração em que a carga está na origem . O resultado é compatível com o obtido no item ?
Ver solução completaQuestão 44
O potencial elétrico devido a uma esfera carregada de raio é
onde é constante e é a distância ao centro da esfera.
Determine o campo elétrico para e .
Determine a carga total da esfera.
Calcule o fluxo através da face superior do cubo de lados mostrado na figura que tem três arestas ao longo dos eixos e . Expresse o resultado em termos da carga total da esfera e de .
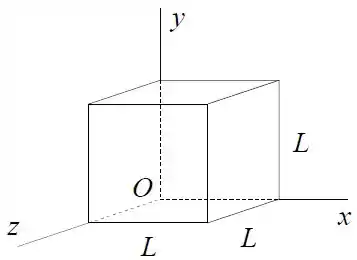
Questão 45
Oito gotas de água idênticas estão todas ao mesmo potencial , relativo ao potencial nulo no infinito. Elas se juntam para formar uma única gota esférica, cujo potencial deve ser:
- ;
- ;
- ;
- ;
- .
Questão 46
Na figura abaixo, temos uma carga puntiforme fixa de carga . A figura mostra três círculos de raios , e . Os pontos e pertencem a trajetória de uma partícula de carga . O trabalho realizado no trecho é:
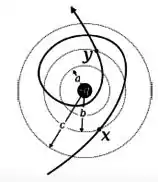
Questão 47
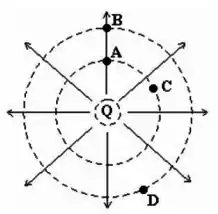
Na figura estão representadas algumas linhas de força do campo criado pela carga . Os pontos A, B, C e D estão sobre circunferências centradas na carga. Assinale a alternativa FALSA:
- Os potenciais elétricos em A e C são iguais.
- O potencial elétrico em A é maior do que em D.
- Uma carga elétrica positiva colocada em A tende a se afastar da carga Q.
- O trabalho realizado pelo campo elétrico para deslocar uma carga de A para C é nulo.
- O campo elétrico em B é mais intenso do que em A.
Questão 48
Duas partículas de cargas e estão separadas por um distância , como mostra a figura abaixo. Nessa situação, podemos afirmar que o trabalho realizado pela força elétrica para trazer uma terceira partícula de carga do infinito para o ponto indicado na figura vale:
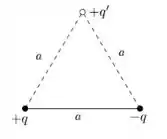
- 0
Questão 49
Qual é a magnitude de um campo elétrico produzido por duas placas paralelas separadas pela distância de ?
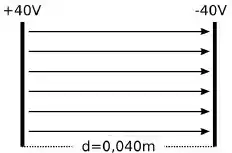
Ver solução completa
Questão 50
O potencial elétrico como função da posição é mostrado na figura.
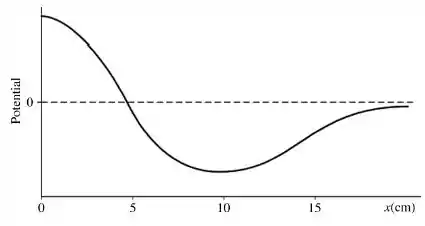
Qual afirmativa sobre o campo elétrico é verdadeira?
A intensidade do campo elétrico é: (i) máxima em ; (ii) nula em e; (iii) mínima em algum ponto no intervalo .
A intensidade do campo elétrico é: (i) mínima em ; (ii) nula em e; (iii) máxima em algum ponto no intervalo .
A intensidade do campo elétrico é: (i) mínima em ; (ii) máxima em e; (iii) nula no infinito.
A intensidade do campo elétrico é: (i) máxima em ; (ii) mínima em e; (iii) nula pelo menos duas vezes no intervalo .
A intensidade do campo elétrico é: (i) mínima em ; (ii) máxima em e; (iii) nula pelo menos duas vezes no intervalo .
Ver solução completaQuestão 51
O potencial elétrico criado pelas três cargas localizadas no arco de círculo de raio , no ponto em que a carga se encontra, vale:
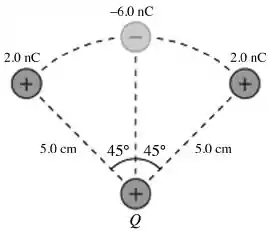
nulo
Ver solução completa
Questão 52
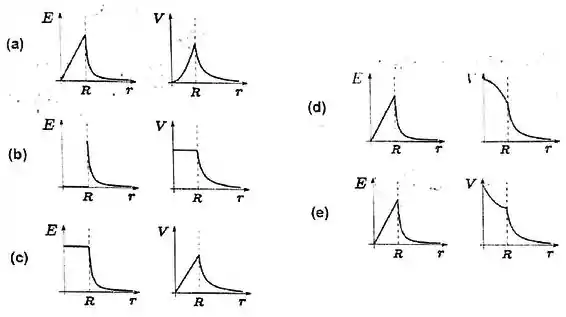
Considere uma esfera maciça com densidade volumar de carga constante (estacionária e uniforme), raio e carga total . Qual das alternativas abaixo melhor representa os gráficos do módulo do campo elétrico e do potencial elétrico, devidos a essa esfera em função da distância ao centro?
Questão 53
O potencial a uma distancia de de uma dada carga elétrica é de . Se em dois vértices de um triângulo equilátero de de lado forem colocadas duas cargas iguais a esta, qual o potencial, em volts, gerado por essas cargas no terceiro vértice?
Ver solução completaQuestão 54
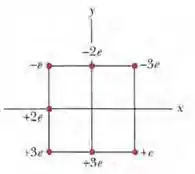
(Capítulo 24.11 – Exercício 44) Na figura abaixo, sete partículas carregadas são mantidas fixas no lugar para formar um quadrado com 4,0 cm de lado. Qual é o trabalho necessário para deslocar para o centro do quadrado uma partícula de carga +6e inicialmente em repouso a uma distância infinita?
Questão 55
Num meio de constante eletrostática igual a , encontra-se uma partícula solitária eletrizada com carga igual a . O potencial elétrico num ponto situado a dessa partícula tem valor igual a:
Ver solução completaQuestão 56
Um grão de poeira tem a forma de uma esfera de raio igual a . Ele possui uma carga negativa uniformemente distribuída sobre seu volume, de forma que o potencial elétrico em sua superfície vale . Considerando que o potencial é nulo em um ponto infinitamente afastado do grão e que , podemos afirmar que a carga total do grão e a intensidade do campo elétrico em sua superfície valem, respectivamente:
(a) e
(b) e
(c) e
(d) e
(e) C e
(f) e
Ver solução completaQuestão 57
Considere as seguintes grandezas físicas:
(I) Campo elétrico
(II) Fluxo de campo elétrico através de uma superfície aberta
(III) Potencial elétrico
São grandezas vetoriais:
(a) Apenas I
(b) Apenas II
(c) Apenas III
(d) Apenas I e II
(e) Apenas I e III
(f) Apenas II e III
(g) I, II e III
(h) Nenhuma delas
Ver solução completaQuestão 58
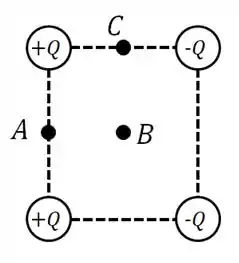
Na figura há quatro cargas puntiformes (de mesmo módulo e sinais mostrados) nos vértices de um quadrado. Considere no infinito. Em qual(is) dos pontos médios ou ) o potencial é nulo?
a) e
b) somente
c) somence
d) somente
e) e .
Ver solução completaQuestão 59
Dois planos infinitos e , paralelos entre si, de densidades superficiais e , estão localizados respectivamente em e .
Calcule detalhadamente o campo elétrico produzido apenas pelo plano , tanto para como para .
De posse desse resultado, encontre o campo elétrico produzido pelos 2 planos na região .
Determine a diferença de potencial entre o plano e o plano , ou seja, .
Ver solução completaQuestão 60
A densidade linear de carga ao longo do eixo é dada por:
onde e são constantes.
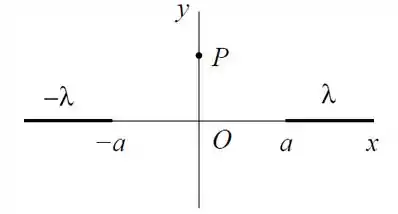
Calcule o campo elétrico num ponto sobre o eixo .
Adotando-se potencial nulo na origem , calcule o potencial num ponto sobre o eixo .
Considere os pontos , e . Qual é o trabalho efetuado pela força elétrica para levar uma carga q ao longo do percurso fechado ?
Ver solução completaQuestão 61
Um corpo de dimensões desprezíveis possui massa e carga . Ele é solto do repouso do alto de uma rampa de altura . Nesta região, o campo gravitacional é constante, e há ainda um campo eletroestático presente. Sabendo-se que o corpo chega ao ponto mais baixo da rampa com velocidade , qual a diferença de potencial eletrostático entre o ponto mais baixo da rampa e o ponto de soltura do corpo?
- Para determinarmos a diferença de potencial devemos conhecer o formato da rampa.
Questão 62
Um anel de raio , com uma carga uniformemente distribuída, é colocado no plano , com seu centro na origem de um sistema de coordenadas cartesianas. Calcule o potencial devido ao anel em um ponto qualquer qualquer do eixo z.
Ver solução completaQuestão 63
13ª questão - Uma esfera condutora de raio está carregada, e sabe-se que a diferença de potencial entre um ponto a do centro e outro a do centro vale . Determine a carga elétrica da esfera.
A)
B)
C)
D)
E)
Ver solução completaQuestão 64
Considere um dipolo elétrico formado por duas cargas de módulo e com sinais opostos, separadas por uma distância . O módulo da posição radial a uma ponto genérico , definida em relação à origem localizada no centro do dipolo, é dado por , que, por sua vez, define o ângulo em relação ao eixo do dipolo (veja figura abaixo).
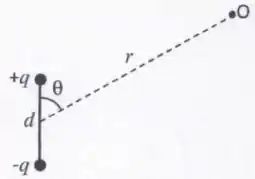
- Num ponto para o qual , calcule o potencial elétrico gerado pelo dipolo em função de e do momento de dipolo .
- A partir do resultado do item a), calcule a componente radial do vetor campo elétrico gerado pelo dipolo no ponto .
- Para uma distância , em que regiões do espaço a componente radial do campo elétrico atinge valores máximos? Discuta seu resultado usando o conceito de linhas de campo elétrico.
Questão 65
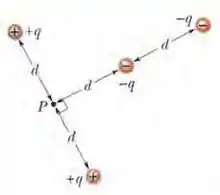
(Capítulo 24.7 – Exercício 17) Na figura abaixo, qual é o potencial elétrico no ponto P devido às quatro partículas se V = 0 no infinito, q = 5,00 fC e d = 4,00 cm?
Questão 66
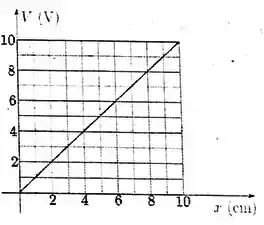
Na figura, representamos um gráfico do potencial elétrico entre duas placas planas, paralelas e extensas, uniformemente carregadas com cargas de sinais opostos, conforme medido ao longo da direção ortogonal às placas, sendo uma das placas escolhida como tendo potencial e posição nulos. Considerando que é o versor na direção positiva do eixo dos , qual é o vetor campo elétrico em qualquer ponto entre as placas?
a)
a)
a)
a)
e)
Questão 67
Esse enunciado utiliza os dados de matrícula dos alunos, mas nós do RA adaptamos para você!
https://www.compadre.org/Physlets/electromagnetism/prob25_5.cfm
O objetivo deste problema é calcular a massa desconhecida da partícula vermelha. As linhas verticais representam superfícies equipotenciais. Ao deslocar a partícula (posicionando o mouse sobre a mesma e mantendo o botão da esquerda apertado) é possível obter informação sobre a sua posição (em metros (m)) e o valor do potencial nessa posição (em Volts (V)). Na animação são mostrados o valor do tempo (segundos (s)) e o valor da velocidade da partícula (m/s).
- Preencha os itens pedidos abaixo, considere que :
- Utilizando , registre a coordenada , o potencial e a velocidade para esse ponto; Tire print da tela mostrando essa posição e respectivas grandezas.
- Deixe a simulação correr até um determinado ponto de sua escolha e registre novamente as grandezas.
- Calculem o valor da massa da partícula. Expliquem seu raciocínio em detalhes. Não pulem passagens.
Questão 68
Uma carga pontual de se move do ponto para o ponto na presença de um
campo elétrico uniforme, como mostrado na figura. Qual das seguintes afirmações sobre a variação da energia potencial do sistema é verdadeira?
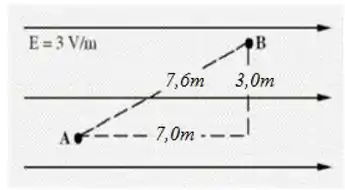
a) A energia potencial aumenta de .
b) A energia potencial diminui de
c) A energia potencial aumenta de
d) A energia potencial diminui de
e) A energia potencial aumenta de .
Ver solução completaQuestão 69
Uma esfera isolante maciça de raio possui uma densidade de carga não uniforme dada pela expressão : onde é desconhecida. Esta esfera isolante é concentricamente circundada por uma fina casca esférica condutora com raios interno e externo , como mostrado na figura.
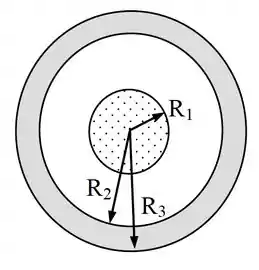
O fluxo elétrico através de uma superfície esférica gaussiana de raio vale . Sabendo que a carga líquida depositada na casca esférica vale :
Calcule o valor da carga total da esfera maciça interna.
Calcule o valor da constante com as unidades.
Calcule a razão entre as densidades de carga interna e externa da casca esférica condutora.
Utilizando a lei de Gauss, calcule o vetor campo elétrico na região .
Calcule a diferença de potencial (), com sinal, entre a esfera interna e a casca esférica.
Ver solução completaQuestão 70
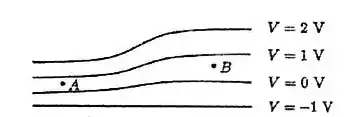
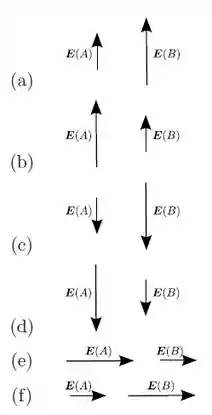
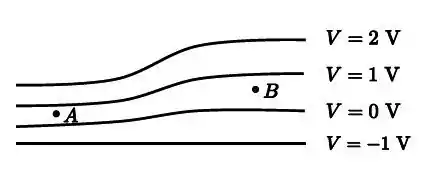
Considere o seguinte corte perpendicular a uma família de quatro superfícies equipotenciais, associadas a um campo eletrostático. Assinale a opção que melhor indica o vetor campo elétrico em cada um dos pontos A e B, respectivamente.
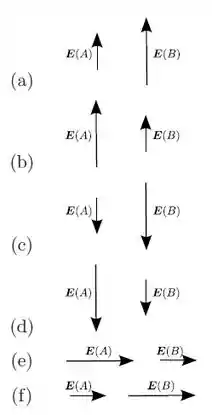
Questão 71
O potencial eletrostático numa região do espaço é dado por , onde e são constantes e é a distância até a origem de um sistema de coordenadas.
Sendo o unitário da direção radial, o campo elétrico nessa região do espaço é dado por:
Ver solução completa
Questão 72
Uma carga elétrica é colocada na origem do eixo , como mostra a figura abaixo.
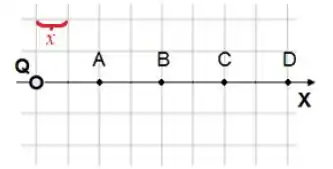
Qual é o valor da razão entre os módulos do potencial elétrico , gerado por esta carga, nos pontos e ?
Ver solução completa
Questão 73
14 - Quatro partículas carregadas são fixadas sobre os vértices de um quadrado de lado a, como mostrado na figura abaixo. Duas delas possuem carga e as outras duas possuem carga . Este quadrado encontra-se sobre o plano XY, com seu centro sobre a origem e seus lados paralelos aos eixos X e Y. O eixo Z é perpendicular ao plano do quadrado e passa por seu centro. Sobre essa situação, assinale a alternativa CORRETA:
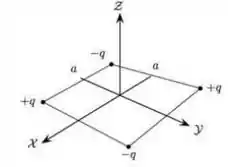
- O campo elétrico resultante produzido pelas quatro partículas tem a mesma intensidade em todos os pontos do eixo X.
- O trabalho realizado pela força elétrica ao trazer as quatro partículas do infinito até a configuração indicada na figura é nulo.
- O campo elétrico resultante produzido pelas quatro partículas é nulo em todos os pontos do eixo Z.
- A força elétrica resultante sobre qualquer uma das partículas devido às outras três é nula.
- Uma partícula carregada abandonada do repouso sobre o centro do quadrado entrará em movimento devido à ação de uma força elétrica.
Questão 74
(Capítulo 24.7 – Exercício 13) Determine (a) a carga e (b) a densidade superficial de cargas de uma esfera condutora de 0,15 m de raio cujo potencial é 200 V (considerando no infinito).
Ver solução completaQuestão 75
Uma esfera condutora de raio R possui uma carga positiva e encontra-se em equilíbrio eletrostático. Considere os três gráficos mostrados na figura abaixo, indicados por I, II e III. Quais destes gráficos melhor representam o comportamento do módulo do campo elétrico E(r) e do potencial elétrico V (r) produzidos pela esfera como função da distância r até o seu centro, respectivamente?
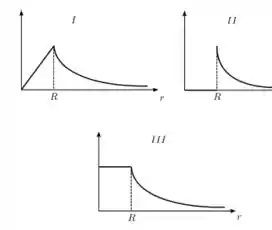
(a) I e II
(b) II e I
(c) I e III
(d) II e III
(e) III e I
(f) III e II
Ver solução completaQuestão 77
Em qual dos pontos indicados no gráfico de potencial em função da posição, o campo elétrico é positivo?
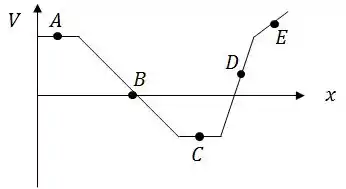
A
B
C
D
E
Ver solução completaQuestão 78
Sobre as linhas de um campo eletrostático não nulo, considere as afirmativas abaixo:
Duas linhas de um campo eletrostático nunca podem se cruzar, caso contrário, o campo ficaria indefinido nos pontos de cruzamento.
O potencial eletrostático aumenta ao longo de uma linha de campo no sentido de sua orientação.
Linhas de campo eletrostático nunca podem ser fechadas, caso contrário o campo não teria caráter conservativo.
São VERDADEIRAS as afirmativas:
e .
.
.
.
e .
e .
, e .
Nenhuma delas.
Ver solução completaQuestão 79
Considere o gráfico que mostra como o potencial eletrostático varia em função da distância radial a partir de um determinado ponto central em cada uma de 4 regiões distintas do espaço. Nas regiões I e III, o potencial é constante, ao passo que, nas regiões II e IV, ele decresce suavemente, como mostra a figura. Podemos afirmar que:
a) A componente radial do campo elétrico é negativa nas regiões I e II
b) A componente radial do campo elétrico é nula nas regiões I e III
c) A componente radial do campo elétrico é negativa nas regiões II e IV
d) A componente radial do campo elétrico é nula nas regiões II e IV
e) A componente radial do campo elétrico é positiva em todas as quatro regiões
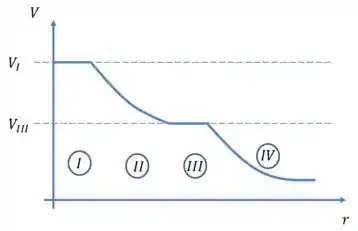
Questão 80
Se o potencial elétrico for nulo em uma região do espaço, o campo elétrico deve ser nulo nesta região.
Verdadeiro ou falso?
Ver solução completaQuestão 81
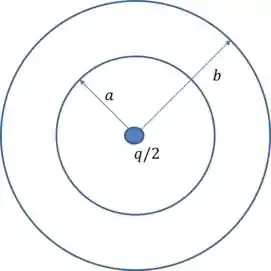
Uma casca condutora esférica, espessa, de raios interno e externo iguais a e , respectivamente, encontra-se em equilíbrio eletrostático e possui carga . Uma partícula, de carga está situada, em repouso, no centro de tal casca. Que relação é válida entre os potenciais e ?
a)
b)
c)
d)
e)
Questão 82
Numa certa região do espaço existe um potencial elétrico dado por:
onde é a distância até a origem do sistema de coordenadas e e são constantes.
Quais são as unidades das constantes α e a no Sistema Internacional de Unidades?
Obtenha o vetor campo elétrico nesta região do espaço.
Quanta carga existe dentro de uma esfera (imaginária) de raio centrada na origem?
Ver solução completaQuestão 83
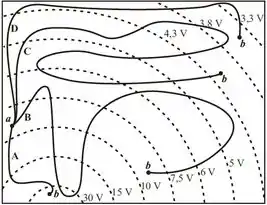
Na figura abaixo, as linhas pontilhadas representam algumas superfícies equipotenciais de uma distribuição de cargas esfericamente simétrica com carga total positiva. Uma partícula de carga positiva pode ser deslocada do ponto até alguns possíveis pontos finais indicados na figura. O deslocamento é feito por meio das trajetórias , , e indicadas. Sobre o trabalho realizado pela força elétrica que atua sobre a partícula ao longo dessas trajetórias (,, e , respectivamente), é CORRETO afirmar que:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Ver solução completaQuestão 84
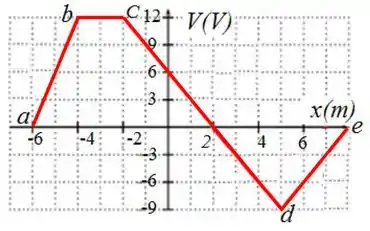
Em uma certa situação, o potencial eletrostático varia ao longo do eixo conforme mostrado na figura abaixo. Assinale a opção que melhor aproxima o valor da componente do campo elétrico (em ) para cada um dos intervalos , , , , respectivamente
Questão 85
Qual das seguintes afirmações sobre situações eletrostáticas é FALSA?
O campo elétrico é nulo em todos os lugares dentro de um condutor.
As superfícies equipotenciais são sempre perpendiculares ao campo elétrico.
Não é necessário realizar trabalho para mover uma carga ao longo de uma superfície equipotencial.
Se o potencial elétrico é constante em toda a região do espaço, então o campo elétrico deve ser nulo nesta região.
Nenhuma força elétrica atua na carga enquanto ela se move ao longo de uma superfície equipotencial.
Ver solução completaQuestão 86
Duas partículas puntiformes, de cargas e , separadas pela distância produzem um potencial no ponto . Sabendo-se que a energia potencial associada a essas duas cargas se anula quando elas estão infinitamente afastadas, conclui-se que:
Nenhuma força atua em uma carga de teste colocada no ponto .
e devem ter o mesmo sinal.
O campo elétrico deve ser zero em .
O trabalho das forças elétricas para trazer as duas partículas do infinito à distância uma da outra é zero.
O trabalho das forças elétricas necessário para trazer uma carga do infinito para o ponto é zero.
Ver solução completaQuestão 87
Um dipolo elétrico é colocado no eixo com em e em .
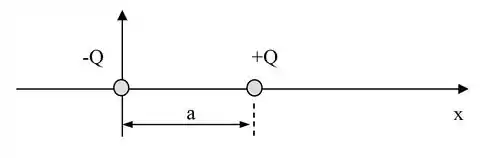
Calcule o potencial elétrico num ponto qualquer do eixo para . Considere o referencial de potencial nulo no infinito.
Apesar do potencial da letra não ser genérico, mesmo assim podemos, a partir dele, encontrar uma componente do campo elétrico. Responda qual é esta componente e calcule-a.
Se uma carga pontual for colocada no ponto , calcule a força elétrica sobre ela e a energia potencial associada à configuração.
Ver solução completaQuestão 88
A figura abaixo mostra equipotenciais ao redor de um par de cargas e .
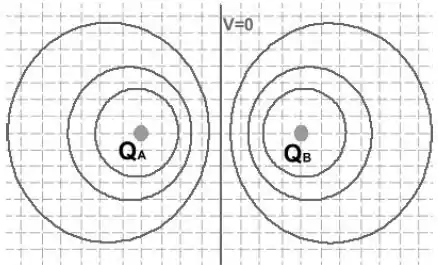
O valor do potencial a meio caminho entre as cargas está indicado na própria figura. Qual das afirmativas abaixo se aplica às cargas?
As duas cargas têm o mesmo sinal e magnitudes iguais.
Nada pode ser dito sobre a natureza das cargas.
As duas cargas têm o mesmo sinal, mas diferentes magnitudes.
As duas cargas têm sinais opostos e mesmas magnitudes.
As duas cargas têm sinais opostos e magnitudes diferentes.
Ver solução completaQuestão 90
Uma esfera condutora de raio possui inicialmente uma carga . Ela encontra-se muito afastada de uma segunda esfera de raio , inicialmente neutra.
A seguir, conectam-se as duas esferas por um fio condutor. Desprezando qualquer acúmulo de carga no fio, após se atingir o equilíbrio eletrostático, as cargas da esfera menor e da esfera maior serão, respectivamente:
e .
e .
e .
e .
e .
Nenhuma das respostas anteriores.
Ver solução completaQuestão 91
Considere a situação onde uma carga puntiforme , de e que está no vácuo, gera um campo elétrico. Podemos afirmar que , em um ponto , situado a da carga , é gerado um potencial elétrico de intensidade: (Considere )
Ver solução completaQuestão 92
Quatro cargas elétricas , , e são colocadas nos vértices de um quadrado de lado . O potencial no ponto , a meio caminho entre as cargas é:
(Use )
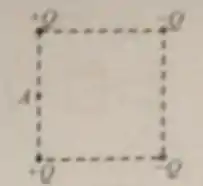
a) .
b) .
c) .
d) .
e) .
Ver solução completaQuestão 93
Uma casca esférica metálica de raio com carga uniformemente distribuída em sua superfície. Quanto vale o potencial no centro da casca esférica?
- Zero
- Nenhuma das alternativas anteriores
Questão 94
Uma distribuição de cargas com densidade linear constante está localizada ao longo do eixo no intervalo conforme a figura.
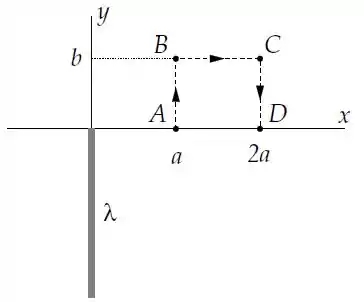
Calcule o vetor campo elétrico num ponto qualquer do eixo com coordenada .
Adotando-se potencial nulo no ponto do eixo com , calcule o potencial elétrico num ponto do eixo com coordenada .
Determine o trabalho que deve ser realizado para levar uma carga do ponto do eixo em ao ponto do eixo em segundo a trajetória mostrada na figura.
Ver solução completaQuestão 95
Uma barra semi-infinita, mostrada na figura ao longo do lado positivo do eixo horizontal , possui carga positiva homogeneamente distribuída com densidade linear .

- Determine o vetor campo elétrico num ponto sobre o lado positivo do eixo .
- Calcule a diferença de potencial eletrostático entre os pontos e sobre o lado positivo do eixo , como indicados na figura.
Questão 96
Uma camada esférica condutora, com carga , tem raio interno e raio externo . No centro da camada, na cavidade interna, há uma carga puntiforme , conforme a figura.
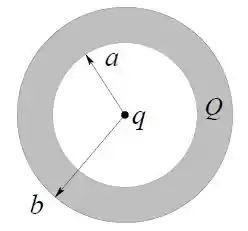
Usando a lei de Gauss e propriedades dos condutores em equilíbrio eletrostático calcule o vetor campo elétrico em todo o espaço.
A partir do campo elétrico calcule o potencial elétrico na região 1 , na região 2 e na região 3 . Defina o potencial no infinito igual a zero.
Ver solução completaQuestão 97
Considere um disco de raio cuja densidade de carga é .
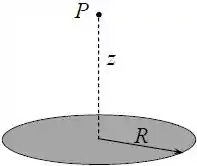
Determine:
O potencial elétrico no ponto , localizado a uma distância acima do centro do disco, conforme a figura ao lado.
O campo elétrico no ponto .
O valor do campo elétrico no limite .
O valor do potencial elétrico no limite .
Ver solução completaQuestão 98
Duas placas planas e infinitas situadas nos planos e estão carregadas com densidades superficiais de carga e , respectivamente, como mostra a figura:
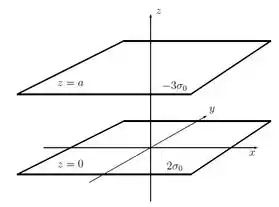
(a) Usando a lei de Gauss, calcule o vetor campo elétrico nas regiões , e .
(b) Calcule a diferença de potencial entre os pontos e .
Ver solução completaQuestão 99
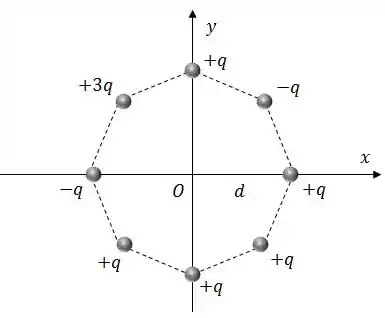
Calcule o campo elétrico no ponto devido à distribuição octogonal de cargas na figura (use o sistema de coordenadas indicado);
Calcule o potencial elétrico em ;
Qual será a aceleração instantânea adquirida por uma partícula de massa , carregada com uma carga positiva , abandonada em ?
Questão 100
Uma carga elétrica está uniformemente distribuída com densidade volumétrica constante em um volume cilíndrico reto, de comprimento infinito e raio (veja a figura abaixo).

Considere que o potencial elétrico é igual a zero em , onde denota a distância até o eixo de simetria do cilindro maciço.
Nessas condições,
Calcule o módulo do campo elétrico para .
Calcule o potencial elétrico para .
Calcule a diferença de potencial entre o ponto e o ponto .
Faça os gráficos do campo elétrico e do potencial elétrico em função de , para .
Ver solução completaQuestão 101
Dois pontos e separados por uma distância encontram-se em uma região onde existe um campo elétrico uniforme, conforme a figura abaixo.
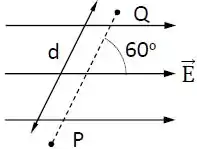
A reta unindo os pontos e faz um ângulo de com o campo, e a diferença de potencial entre eles é . Qual é o módulo do campo elétrico?
;
;
;
;
;
;
Ver solução completaQuestão 102
Na figura abaixo há quatro cargas puntiformes (de mesmo módulo e sinais contrários) no vértices de um quadrado. Considere no infinito. Em qual(is) dos pontos médios (A, B ou C) o potencial é nulo?
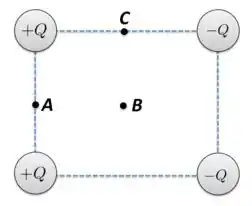
- A e B;
- somente A;
- B e C;
- somente B;
- somente C.
Questão 103
Uma esfera condutora de raio e com carga é envolta por uma camada esférica isolante de raio interno e externo com densidade de carga volumétrica constante.
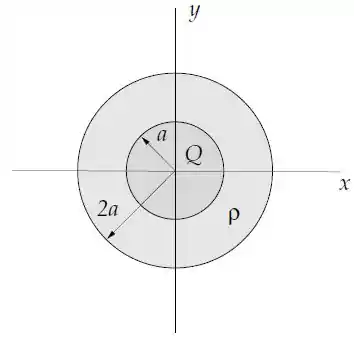
Determine o vetor campo elétrico em todo o espaço;
Determine o potencial elétrico em todo o espaço. Adote potencial nulo no infinito;
Ver solução completaQuestão 104
Considere os três objetos, , mostrados na figura, na presença do campo eletrostático gerado pela carga pontual positiva. Todas as linhas orientadas (“com setinhas”) mostradas são linhas de campo elétrico. Qual a única afirmação verdadeira?
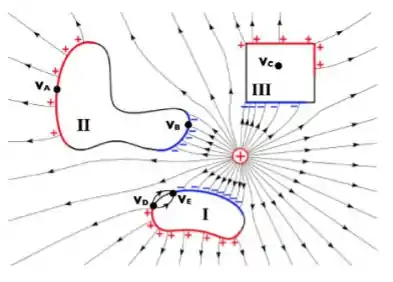
é um condutor e
é um condutor
é um condutor e
é um condutor e
é um condutor e
é um condutor e
Ver solução completaQuestão 105
Duas partículas carregadas, fixas em suas posições, produzem um campo eletrostático nulo em um ponto do espaço. Sobre essa situação, considere as afirmativas abaixo:
- O ponto deve estar necessariamente sobre a linha que passa pelas duas partículas.
- As duas partículas devem ter necessariamente cargas de sinais opostos.
- O potencial eletrostático deve ser necessariamente nulo no ponto .
São VERDADEIRAS as afirmativas:
- I
- II
- III
- I e II
- I e III
- II e III
- I, II e III
- Nenhuma delas.