Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 13.Exercícios e Problemas - Ex. 76
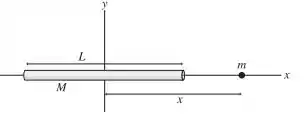
A FIGURA PD13.76 mostra uma partícula de massa m a uma distância x do centro de um cilindro muito fino, de massa M e comprimento L. A partícula se encontra fora do cilindro, de modo que x > L/2.
a. Calcule a energia potencial gravitacional das duas massas.
b. Use o que você sabe sobre a relação entre força e energia potencial para determinar o módulo da força gravitacional exercida sobre m quando ela estiver na posição x.
Passo 1
Queremos calcular a energia potencial de interação entre uma massa e um corpo extenso. Como podemos fazer isso? Sabemos que a energia potencial de interação entre duas partículas, uma de massa e a outra de massa é dada por:
sendo a constante universal da gravitação e a distância entre as partículas. Podemos utilizar tal expressão, considerando que o corpo rígido é formado por infinitas “partículas”, cada uma com massa . Veja na figura abaixo.
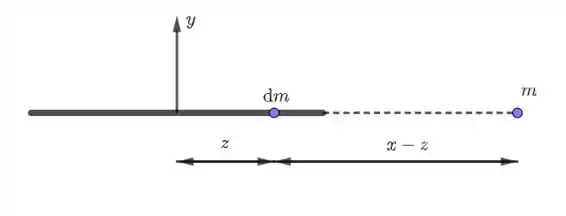
A energia potencial das partículas de massas e é:
A seguir, devemos somar todas as contribuições de todas as partículas da barra. Como fazemos isso? Integrando, logicamente :D
Por fim, o item b) nos pede para relacionar a energia potencial com a força. Lembremos que a força gravitacional é uma força conservativa. Assim, há uma relação entre a força e energia potencial dada por
Passo 2
-
Okay, vamos agora usar o fato de que a barra possui densidade linear constante:
Assim, a massa pode ser relacionada com seu comprimento por:
Assim, temos:
Integrando, temos:
Notemos que:
Dessa forma, temos que:
onde usamos que .
Passo 3
- Temos que
é a expressão da força.