Exercícios de Energia Potencial Gravitacional - Lista de Exercícios Resolvida

Dez dias após seu lançamento para Marte em dezembro de 1998, a espaçonave Mar Climate Orbiter (massa igual a ) estava a uma distância de da Terra e se deslocava com velocidade igual a em relação à Terra. Nesse momento, qual era a energia potencial gravitacional do sistema espaçonave-Terra?

Dados:

a) Se tomamos como zero a energia potencial de um corpo de e a Terra, quando os dois estão separados de uma distância infinita, qual é a energia potencial quando o corpo está na superfície da Terra?

b) Determine a energia potencial do mesmo corpo a uma altura, acima da superfície da Terra, igual ao raio da Terra.

Dados:

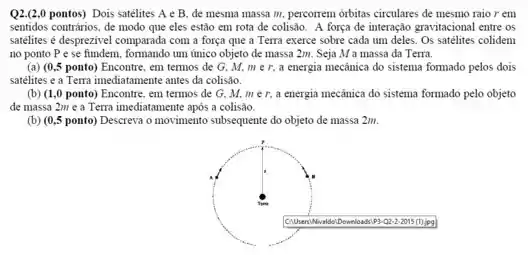
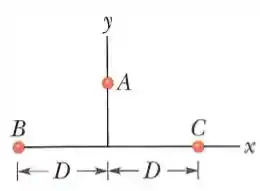
Uma partícula (partícula , de massa ) pode ser deslocada ao longo de um eixo desde uma distância infinita até a origem. A origem está localizada no ponto médio entre as partículas e , que têm massas iguais , e o eixo é perpendicular à linha que liga essas duas partículas. A distância é . O gráfico mostra a energia potencial do sistema de três partículas em função da posição da partícula no eixo , sendo que para a direita a curva tende assintoticamente ao valor de quando . Quais são os valores de e ?

.

Considere um projeto de lançamento onde satélites são lançados como projéteis. Seja a constante gravitacional, e e , o raio e a massa da Terra, respectivamente.

(a) Ignorando a atmosfera e a rotação terrestre, deduza a velocidade com que um projétil deve ser lançado para atingir uma altitude máxima de medida a partir da superfície.

(b) Calcule a razão entre a velocidade de escape de um satélite lançado da Terra e a velocidade de escape do satélite lançado de um planeta cujo raio vale e cuja massa é

O gráfico abaixo representa a aceleração da gravidade (em ) em função da distância ao centro de um asteróide esférico cujo raio é de

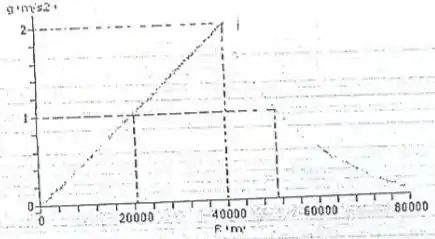
(a) Calcule a velocidade de escape de um corpo neste asteroide.

(b) Até que distância da superfície irá o corpo se ele deixar a superfície do asteroide com uma velocidade radial de ?

Um corpo está gravitacionalmente ligado a outro se:

1. A energia potencial é negativa.
2. As energias cinética e potencial são ambas negativas.
3. A energia mecânica é negativa.
4. A energia mecânica é positiva.
5. A energia mecânica é zero.

Um objeto é abandonado do repouso a de altura da superfície da Terra. Despreze a resistência do ar.

Dados: ; (raio da Terra); (massa da Terra).

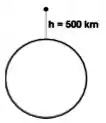
1. Qual é a velocidade do objeto quando atinge o solo?
2. Qual seria sua velocidade se a Terra fosse considerada plana?
3. Qual é o erro percentual cometido supondo a Terra plana?

Um objeto de massa é abandonado de uma altura acima da superfície de um planeta de massa e raio . Qual a rapidez do objeto ao chocar-se com a superfície do planeta?

Considere dois satélites idênticos, denotados por e , de massa , que estão orbitando o planeta Terra, que estão descrevendo órbitas circulares de raios e (). Considere apenas a interação gravitacional entre a Terra e cada satélite, e que os satélites podem ser considerados esféricos, qual a única verdadeira das afirmativas a seguir?

a) A energia cinética do satélite na órbita de raio é maior do que a do de raio

b) O trabalho realizado pela força gravitacional que a Terra exerce sobre o satélite em uma volta completada órbita é maior do que aquele realizado pela força gravitacional que a Terra exerce sobre o satélite em uma volta completa da órbita.

c) O trabalho realizado pela força gravitacional que a Terra exerce sobre o satélite em uma volta completada órbita é menor do que aquele realizado pela força gravitacional que a Terra exerce sobre o satélite em uma volta completa da órbita.

d) O período da órbita dos dois satélites é igual

e) A energia potencial do sistema Terra-satélite 2 é maior do que a energia potencial do sistema Terra-Satélite 1

. Uma partícula de massa se encontra a uma distância de uma estrela de massa e raio

, porém com uma pequena velocidade em direção a estrela. Leve em consideração que inicialmente . Ao atingir a estrela, qual aproximadamente a variação de energia

potencial da partícula a partir do momento inicial?

Zero

Dois cilindros, de mesma massa e raio externo , sendo um oco com paredes finas e o outro sólido, rolam sem deslizar para baixo em uma superfície cilíndrica com formato circular, com raio muito maior do que , e que se conecta de forma contínua a um plano horizontal. Ambos partem do repouso, da mesma altura em relação ao plano horizontal, no mesmo instante. Sobre o estado de movimento dos dois objetos, quando chegam ao plano horizontal, podemos afirmar que:

1. Ambos têm a mesma energia cinética de translação.
2. Ambos têm a mesma energia cinética de rotação.
3. Os dois objetos chegam juntos ao plano horizontal, pois partem do repouso da mesma altura , com a mesma energia potencial gravitacional.
4. O cilindro oco chega primeiro ao plano horizontal porque seu momento de inércia é maior que do cilindro sólido.
5. O cilindro sólido chega primeiro ao plano horizontal porque seu momento de inércia é menor que do cilindro oco.

Um projétil é disparado verticalmente para cima, a partir da superfície da Terra, com uma velocidade inicial de 10 km/s. Desprezando a resistência do ar, calcule:

a) A distância h acima da superfície da Terra que o projétil alcança;

b) A velocidade de escape do projétil (aproximadamente);

c) Faça o gráfico da energia potencial gravitacional a partir da superfície da terra. Indique

claramente as escalas do gráfico mostrando aproximadamente o valor de h.

Dados aproximados:

massa da Terra ; raio da Terra ; constante de gravitação universal .

Um planeta de massa m orbita uma estrela de massa M. Considerando a massa da estrela muito maior que a do planeta, podemos descrever a energia mecânica E do sistema (constante) em termos do momento angular L (constante), da distância entre o planeta e a estrela r e de sua velocidade radial :

Onde G é a constante gravitacional universal. Note que a contribuição da velocidade angular para a energia cinética é completamente descrita em termos do momento angular L e do momento de inércia I = mr2. A combinação desse termo com a energia potencial gravitacional dá origem a um potencial efetivo, Ue(r), dependente apenas de r.

(a) [1,0] Qual a distância re, correspondente ao mínimo da energia potencial efetiva?

(b) [1,0] Escreva a equação diferencial do movimento para pequenas oscilações ao redor de re, em termos de r’ = r - re.

(c) [1,0] Calcule a frequência de oscilação ao redor de re.

Dê suas respostas em termos de M, m, L, G.

Em uma esfera maciça e homogênea de massa M e raio 2R centrada na origem foram feitas duas cavidades esféricas de raio R. Os centros das cavidades esféricas estão nas posições e , como ilustrado na figura abaixo. Sabendo que uma massa m está na posição, faça o que é pedido abaixo.

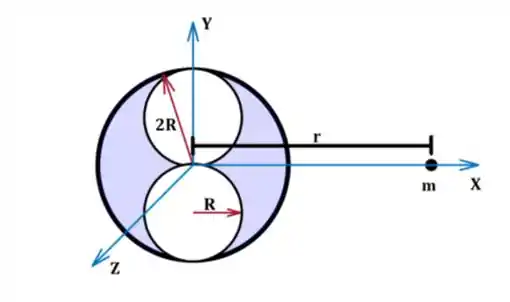
a) Calcule a força gravitacional que atua na partícula de massa m.

b) Admita que a partícula de massa m está em uma órbita circular de raio r > R no plano XZ. Calcule o período de rotação.

c) Calcule a energia potencial gravitacional do sistema ilustrado na figura ao lado.

[Questão 12]

A figura ao lado mostra um foguete de massa que descreve uma órbita elíptica em torno da Terra, onde é a distância da Terra em relação ao centro da elipse e é o semi-eixo maior da elipse. A massa da Terra é . A única força que atua sobre o foguete é a atração gravitacional do planeta. No ponto A, o foguete tem velocidade de módulo . Com base nessas informações, responda as questões 11, 12 e 13.

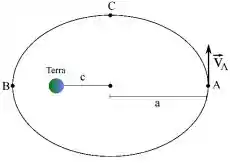
No ponto A da órbita, o foguete ilustrado na figura anterior aciona seus propulsores por alguns segundos, gerando uma força que o coloca em uma órbita circular de raio . Considerando que a força gerada pelos propulsores é instantânea e, portanto, que a distância do foguete ao planeta não muda durante sua aplicação, determine a variação de energia mecânica gerada pelos propulsores.

(A)

(B)

(C)

(D)

(E)

Na superfície da Terra, você consegue dar um pulo de de altura. Qual altura você alcançaria na superfície do asteróide Juno, que tem massa e raio médio estimados em e , respectivamente?

Dados:

Raio da Terra:

Massa da Terra:

Um satélite de massa igual a move-se, inicialmente, numa órbita aproximadamente circular a acima da superfície da Terra. Por várias razões, o satélite perde energia mecânica à taxa média de por revolução orbital. Adotando a aproximação razoável de que a trajetória seja “um círculo cujo raio diminui lentamente”, determine a distância do satélite à superfície da Terra após a revolução orbital.

Dados:

Constante gravitacional:

Raio da Terra:

Massa da Terra:

Um sistema binário de estrelas consiste em duas estrelas idênticas, cada uma com massa , girando em torno do centro de massa do sistema. As estrelas estão em pontos opostos de uma mesma órbita circular de raio . Determine:

a) a intensidade da força gravitacional de uma estrela sobre a outra;

b) o módulo da velocidade orbital de cada estrela e o período da órbita;

c) a energia necessária para separar as duas estrelas até uma distância infinita.

Um determinado sistema triplo de estrelas consiste em duas estrelas, cada uma de massa , que giram na mesma órbita circular em torno de uma estrela central de massa . As duas estrelas situam-se nos extremos opostos de um diâmetro da órbita circular. Qual o período de revolução de cada estrela e sua energia mecânica?

Um satélite artificial da Terra é transferido de uma órbita circular de raio para uma órbita circular de raio . Sejam: o trabalho realizado pela força gravitacional; a energia cinética e a energia potencial gravitacional. Na transferência de órbita (), é correto afirmar que:

(A) é positivo, aumenta e aumenta.

(B) é positivo, aumenta e diminui.

(C) é positivo, diminui e aumenta.

(D) é negativo, aumenta e diminui.

(E) é negativo, diminui e aumenta.

A energia necessária para levar um satélite até acima da superfície da Terra é maior do que a necessária para colocá-lo em órbita, uma vez que ele já esteja naquela altura?

Dados:

Constante gravitacional:

Raio da Terra:

Massa da Terra:

4 – No espaço sideral, a esfera , com de massa, está na origem de um eixo e a esfera , com de massa, está no mesmo eixo em . A esfera é liberada a partir do repouso enquanto a esfera é mantida fixa na origem.

(a) Qual é a energia potencial gravitacional sistema das duas esferas no momento em que a esfera é liberada?

(b) Qual é a energia cinética da esfera após ter se deslocado em direção à esfera ?

Um satélite artificial encontra-se em uma órbita circular de raio em torno da Terra quando ativa seus motores e passa a uma órbita, também circular, de raio (). É correto afirmar que:

(a) A energia potencial associada à força gravitacional que a Terra exerce sobre o satélite aumenta na mudança de órbita.

(b) O trabalho realizado pela força gravitacional que a Terra exerce sobre o satélite é nulo na mudança de órbita.

(c) A energia cinética do satélite permanece inalterada na mudança de órbita.

(d) A energia mecânica do satélite permanece constante na mudança de órbita.

(e) A força gravitacinal que a Terra exerce sobre o satélite realiza trabalho positivo na mudança de órbita.

Dois planetas têm a mesma massa, M. Cada planeta tem uma densidade constante, mas a densidade do planeta 2 é 8 vezes aquela do planeta 1. Objetos idênticos de massa m são colocados sobre as superfícies dos planetas. Qual é a relação aproximada entre a energia potencial gravitacional no planeta 1 e no planeta 2?

a)

b)

c)

d)

e)

Considere um planeta movendo-se numa órbita somente sob ação do campo gravitacional do Sol. Tomando o centro de massa do Sol como referência, assinale a afirmativa incorreta:

Obs: Periélio: ponto da órbita mais próximo do Sol;

Afélio: ponto da órbita mais longe do Sol.

a) A componente angular da velocidade no periélio e afélio é nula.

b) A componente angular da aceleração é sempre zero.

c) O raio vetor varre áreas iguais em tempos iguais, o que corresponde à conservação do momento angular.

d) Energia e momento angular são conservados.

e) O módulo da velocidade no periélio é maior que a no afélio.

Em um sistema binário consistindo de duas estrelas de mesma massa, onde a energia potencial gravitacional é igual a zero? Escolha uma

(a) Exatamente a meio caminho entre as estrelas

(b) Em nenhum ponto

(c) Em um ponto infinitamente afastado das estrelas

(d) Em um ponto bem próximo de uma delas

(e) Ao longo da mediatriz da reta ligando as estrelas