Uma fina haste de vidro é dobrada em um semicírculo de raio . Uma carga é uniformemente distribuída ao longo da metade superior e uma carga é uniformemente distribuída ao longo da metade inferior, conforme mostrado na Fig. 26-28. Determine o campo elétrico em , o centro do semicírculo.
Passo 1
E aí galerinha, vamos destruir essa questão comigo? Vamos láaaa!
Vamos desenhar um pequeno esboço do problema. Teremos a seguinte situação:
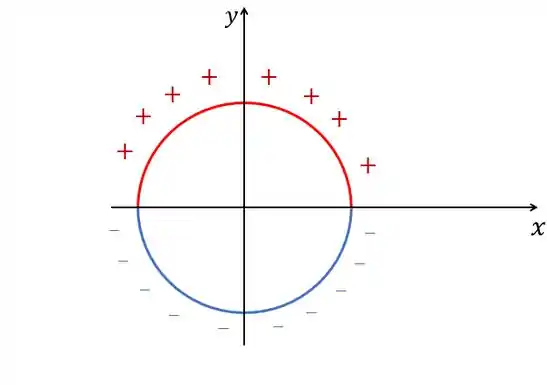
O nosso problema pede pra gente calcular o campo elétrico no centro do círculo, pra isso, podemos ver que teremos tanto uma contribuição de cima quanto de baixo do anel, no centro.
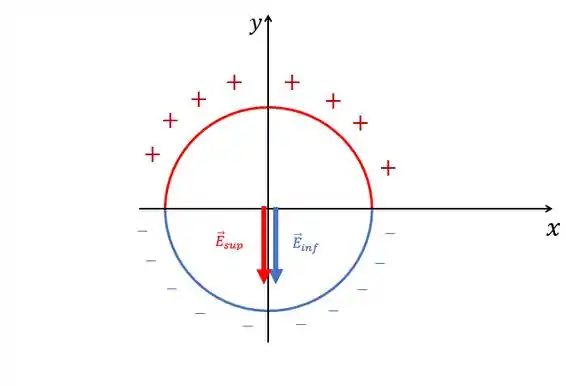
Malandramente a gente pode perceber uma certa simetria no problema, consegue visualizar? As cargas produzirão, no centro do anel, um campo elétrico. Mas, a medida que a gente avalia todas as cargas distribuídas pelo anel, teremos uma resultante apenas na direção vertical, já que há uma simetria em torno de ! Esse tipo de análise pode simplificar muito a nossa vida e nossas contas.
Podemos encontrar o campo elétrico produzido pelas duas partes avaliando a contribuição de cada infinitésimo de carga distribuído pelas duas superfícies. Dessa forma, teremos uma espécie de densidade linear de carga pelas duas metades do anel, dada por:
Com isso em mente, vamos para a resolução da questão!
Passo 2
Primeiro, vamos analisar a parte superior. Imagina uma pequena carga do semi anel superior. Esse pequeno elemento de carga produzirá, no centro, um campo elétrico com a seguinte expressão:
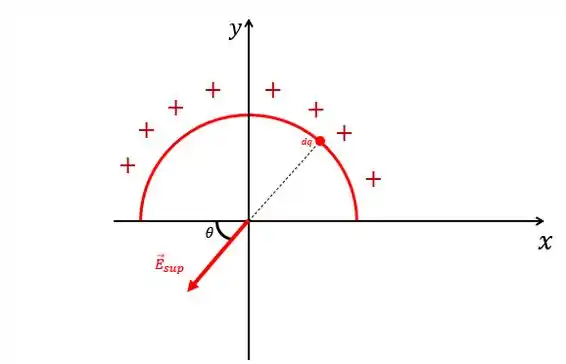
Se imaginarmos agora que essa carga vem justamente de uma porção do comprimento do semi anel, podemos deduzir essa porção como sendo:
Dessa forma, nossa densidade linear de carga será:
Ou melhor:
Dessa forma, podemos substituir na nossa expressão para o campo elétrico, na forma:
Como queremos a contribuição total, devemos ter em mentes que as contribuições na direção serão simétricas, ou seja, só teremos resultante em . Nossa integral será em relação a componente vertical do campo elétrico.
Sendo assim, basta que a gente integre a expressão pro nosso infinitésimo de campo elétrico sob todo o comprimento do anel. Em outras palavras, vamos integrar a expressão de .
Teremos então que:
Finalmente, temos que:
Passo 3
Analisando a parte inferior, realizaremos o mesmo raciocínio, a única diferença é que teremos uma carga negativa, apenas.
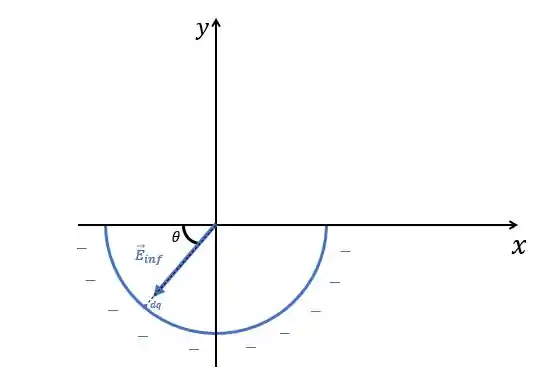
Pela simetria do problema, novamente teremos apenas contribuições em . Dessa forma, nosso campo total será:
Nossa componente vertical será:
Simplificando nossa integral, teremos:
Finalmente:
Passo 4
Nosso campo elétrico resultante será: