Uma força atuando sobre uma partícula de 2,0 kg do plano xy, nas coordenadas (x, y), é dada por , onde b é uma constante positiva e r é a distância da partícula à origem. (a) Mostre que a magnitude da força é inversamente proporcional a e que sua orientação é antiparalela (oposta) ao raio vetor . (b) Se , encontre o trabalho realizado por esta força enquanto a partícula se move de (2,0 m; 0,0 m) até (5,0 m; 0,0 m) em um caminho reto. (c) Encontre o trabalho realizado pela força sobre a partícula quando esta completa uma volta em um círculo de 7,0 m de raio centrado na origem.

Só que é a distância de um ponto qualquer até a origem. Olha nessa figura:

Usando Pitagoras, podemos escrever essa distância como . Substituindo isso no módulo de :

Isso mostra que a magnitude da força é inversamente proporcional a .

Para ver que é oposta ao vetor (que é o vetor posição/raio) podemos pegar a definição de :

Percebe que aparece esse termo que é o próprio vetor posição . Então vamos substituir:

Essa expressão mostra que as componentes de são proporcionais a . Ou seja, que é paralela a .

E percebe também que tem um sinal de menos ali. Isso nos diz que que as componentes de são têm sinal inverso às componentes de . Ou seja, a força é na verdade antiparalela ao vetor , que é o mesmo que ser oposta ao vetor posição.

Letra (b)

Percebe que se a partícula saiu de e foi para só houve movimento no eixo . Então a gente pode usar a expressão para trabalho unidimensional com força variável (já que nossa força depende de e ).

Vamos calcular o trabalho realizado apenas na direção , porque só há movimento nesse eixo, e assim só há trabalho nesse eixo. A fórmula é:

O ponto inicial é e o ponto final é . Vamos substituir isso:

A componente da nossa força é:

Como nosso movimento é somente horizontal, :

Substituindo isso na nossa integral:

Aí agora é calcular essa integral:

Letra (c)

Queremos o trabalho realizado se a trajetória for circular. Agora pensa comigo: vimos que o vetor posição é sempre antiparalelo à força. Esse é o vetor posição de um ponto genérico:

Ou seja, a força aponta sempre para origem. So nosso círculo está centrado na origem, a força aponta pra o centro do círculos sempre:

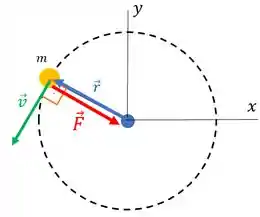
Se a força está sempre apontando para o centro do círculo, ela é sempre perpendicular a trajetória da partícula.

Se a força é sempre perpendicular ao movimento da partícula, ela nunca está na direção desse movimento.

Eeee se o movimento e a força nunca estão na mesma direção, não há trabalho. Logo para esse caso,