Exercícios de Trabalho - Lista de Exercícios Resolvida
Questão 1
Um disco horizontal gira em torno de um eixo vertical que passa pelo seu centro, com velocidade angular constante. Coloca-se um corpo de pequenas dimensões e massa sobre o disco a uma distância de do seu centro. Verifica-se que o atrito entre o corpo e a superfície do disco é suficiente para que ele permaneça na mesma posição do disco em que foi colocado. Ou seja, ele não desliza sobre o disco. O disco dá uma volta completa no intervalo de tempo . Sabendo-se que o coeficiente de atrito estático entre o corpo e a mesa é , o trabalho realizado pela força de atrito numa volta completa é igual a:
Questão 2
A figura mostra uma bola de massa rolando sem deslizamento numa trajetória espiral descendente no interior de um cone oco e numa região de campo gravitacional uniforme . O trabalho realizado pela força de contato da parede sobre a bola é:
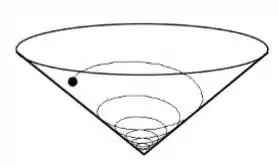
(a) zero.
(b) depende da aceleração gravitacional local e da massa da bola.
(c) depende da forma da trajetória espiral
(d) positivo.
(e) negativo.
Ver solução completaQuestão 3
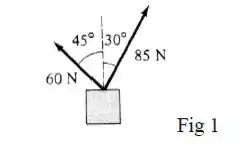
Uma partícula move-se no plano em uma trajetória retilínea ao longo do eixo , da origem ao ponto , e a seguir ao longo de uma trajetória retilinea do ponto ao ponto , como indicado na figura. Durante todo o percurso agem sobre a partícula três forças constantes , e de mesmo módulo. Os ângulos que as forças , e fazem com o eixo são, respectivamente, , e . Denotando os respectivos trabalhos das três forças em todo o percurso de a por , e , podemos afirmar que
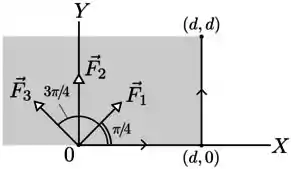
- , e ;
- , e ;
- , e ;
- , e ;
- O trabalho realizado por cada uma das três forças é o mesmo.
Questão 4
Uma partícula de sofre um deslocamento de Durante esse deslocamento , uma força constante atua sobre a partícula.
- Determine o trabalho realizado por para esse deslocamento.
- Determine a componente de na direção desse deslocamento.
Questão 5
Uma caixa de é levantada de uma altura de , a partir do repouso, por uma força aplicada vertical de . Encontre o trabalho realizado sobre a caixa pela força aplicada.
Ver solução completaQuestão 6
Uma partícula move-se no plano horizontal sob a ação de uma força constante . Em um dado instante a sua posição é e em um instante posterior a sua posição é , onde e são constantes. O trabalho realizado por essa força do instante inicial ao final é
- ;
- ;
- ;
- ;
- ;
Questão 7
Duas molas idênticas, de constante elástica e comprimento relaxado , estão conectadas a um bloco, conforme ilustrado na figura . Nesta configuração, as molas estão estendidas a um comprimento . Uma força externa é capaz de arrastar o bloco para a direita, percorrendo uma distância , e mantê-lo nesta posição (ver figura ). Calcule o trabalho realizado pela força externa sobre o bloco.
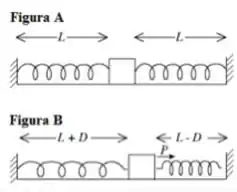
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 8
A figura mostra dois caminhos ( e ) ao longo dos quais uma partícula é levada da origem até o ponto . Nessa região há uma força . Pode-se dizer do trabalho realizado por :
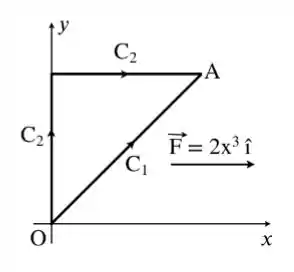
(a) que depende da massa da partícula.
(b) que é maior ao longo do caminho .
(c) que ao longo de e são iguais numericamente à área do triângulo delimitado pelos 2 caminhos.
(d) que é igual para os dois caminhos.
(e) que é maior ao longo do caminho .
Ver solução completaQuestão 9
A figura mostra uma bola de massa rolando sem deslizamento numa trajetória espiral descendente no interior de um cone oco e numa região de campo gravitacional uniforme . O trabalho realizado pela força de contato da parede sobre a bola é:
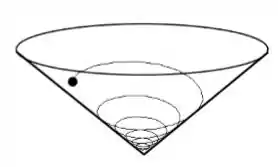
(a) zero.
(b) depende da aceleração gravitacional local e da massa da bola.
(c) depende da forma da trajetória espiral
(d) positivo.
(e) negativo.
Ver solução completaQuestão 10
O coração humano é uma bomba potente e extermamente confiável. A cada dia ele recebe e descarrega cerca de de sangue. Suponha que o trabalho realizado pelo coração seja igual ao trabalho necessário para ele elevar essa quantidade de sangue até uma altura igual à altura média de uma mulher norteamericana (). A densidade (massa por unidade de volume) do sangue é igual a .
a) Qual é o trabalho realizado pelo coração em um dia?
Ver solução completaQuestão 11
Inicialmente um carro de massa desloca-se na direção com velocidade . Para desviar de um obstáculo aplica-se uma força constante . O carro sofre um deslocamento num intervalo de tempo entre os pontos A e B, conforme indicado na figura abaixo. Escolha o item correspondente ao trabalho realizado por entre os pontos A e B.
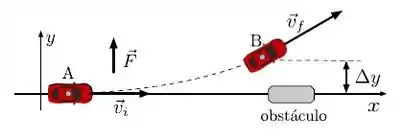
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 12
Você e sua bicicleta possuem massa total igual a . Quando você atinge a base de uma ponte, está se deslocando com uma velocidade de . No topo da ponte você subiu uma distância vertical de e sua velocidade diminuiu para . Despreze o trabalho realizado pelo atrito e qualquer ineficiência na bicicleta ou em suas pernas.
a) Qual o trabalho total realizado sobre você e sua bicicleta quando você vai da base ao topo da ponte?
Ver solução completaQuestão 13
Ainda considerando o gráfico da figura anterior (que mostra a energia potencial em função da distância de um objeto em movimento ao longo do eixo x), considere agora que uma partícula é posta em repouso no ponto B.
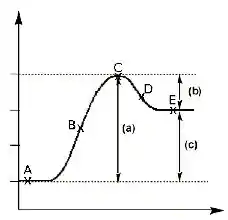
Em que ponto sua velocidade será máxima?
a) ponto C
b) ponto A
c) ponto E
d) x → infinito
e) ponto B, ao retornar
Ver solução completaQuestão 14
Você aplica uma força constante a uma caixa de 2,5 kg que desliza no chão de uma fábrica. A caixa desliza de uma posição inicial a uma posição final em 15,0 segundos. Para esse deslizamento, calcule (a) o trabalho realizado pela força constante sobre a caixa.
Ver solução completaQuestão 15
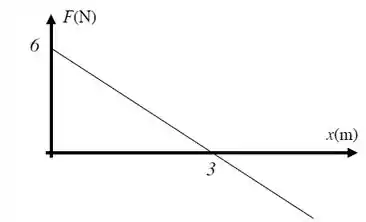
O gráfico mostra a componente de uma força aplicada a um corpo ao longo do deslocamento como uma função da magnitude do deslocamento. Determine o trabalho realizado pela força durante o intervalo de 2 a 10 m.
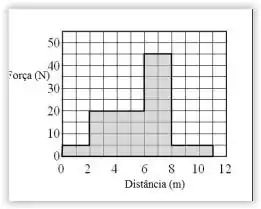
(A) 140 J
(B) 180 J
(C) 195 J
(D) 200 J
(E) 560 J
Ver solução completaQuestão 16
Um bloco é puxado por um fio por 7,0 m por uma superfície horizontal sem atrito, conforma a figura. A tensão no fio é de 40 N e o trabalho realizado por esta força sobre o bloco é igual a 247 J. Qual é o ângulo θ que o fio faz com a horizontal?
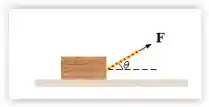
(A) 28°
(B) 45°
(C) 51°
(D) 62°
(E) 88°
Ver solução completaQuestão 17
No diagrama representado na figura abaixo temos uma amostra de gás ideal que pode de expandir de para enquanto sua pressão diminui de para , através dos processos expressos pelos caminhos .
- Ordene em ordem crescente de magnitude os trabalhos realizados pelo gás desde o estado inicial até o estado final através dos processos . Justifique sua resposta.
- Calcule a diferença entre o calor envolvido no processo e no processo . em termos de .
- Calcule a razão entre as temperaturas no estado final e no estado inicial .
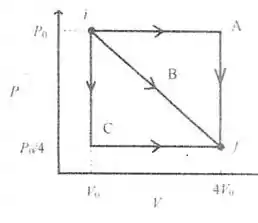
Questão 18
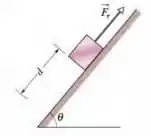
. Um bloco de massa é deslocado para cima, por uma força constante, uma distância ao longo de um plano inclinado. O plano está inclinado de em relação à horizontal, e a força faz um ângulo com a vertical. Determine o trabalho realizado pela força ao longo do deslocamento. Utilize o sistema de coordenadas indicado na figura.
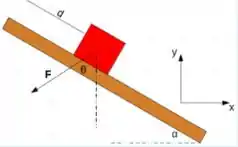
Questão 19
Um bloco de gelo flutuante é colhido por uma correnteza que aplica ao bloco uma força , fazendo com que o bloco sofra um deslocamento . Qual é o trabalho realizado pela força sobre o bloco durante o deslocamento?
Ver solução completaQuestão 20
Um disco com momento de inércia de e raio de 0,25 gira em torno de um eixo fixo perpendicular ao disco e passando pelo seu centro. Uma força de 2,0 N é aplicada tangencialmente à borda do disco. Até o disco completar meia volta, o trabalho feito pela força é aproximadamente:
a) 10 J
b) 1,6 J
c) 40 J
d) 2,5 J
e) 6,3 J
Ver solução completaQuestão 21
Uma partícula é deslocada de no sentido negativo do eixo x mediante a aplicação da força constante . Qual o trabalho realizado por essa força sobre a partícula?
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 22
Uma máquina transporta um pacote de de uma posição inicial em até uma posição final em . A força constante aplicada pela máquina ao pacote é . Para esse deslocamento, determine o trabalho realizado pela força da máquina sobre o pacote e a potência média dessa força.
Ver solução completaQuestão 23
Uma moeda desliza sobre um plano sem atrito em um sistema de coordenadas , da origem até o ponto de coordenadas , sob o efeito de uma força constante. A força tem um módulo de e faz um ângulo de no sentido anti-horário com o semi-eixo positivo. Qual é o trabalho realizado pela força sobre a moeda durante esse deslocamento?
Ver solução completaQuestão 24
Um trenó e seu ocupante, com uma massa total de descem uma encosta e atingem um trecho horizontal retilíneo com uma velocidade inicial de . Se uma força desacelera o trenó até o repouso a uma taxa constante de , qual é o módulo da força. que distância o trenó percorre até parar e que trabalho é realizada pela força sobre o trenó? Quais são os valores de , e se a taxa de desaceleração fosse de ?
Ver solução completaQuestão 25
Um galão de azeite de se move ao longo do eixo de acordo com a equação , com em metros e em segundos, impulsionado por uma força . Determine
o vetor no instante .
Ver solução completaQuestão 26
Um trenó é rebocado por uma pessoa sobre um campo gelado. A pessoa puxa o trenó (massa total de ) com uma força de , fazendo um anglo de com a horizontal. Determine:
- O trabalho efetuado pela pessoa
- A velocidade do trenó depois de cobrir cinco metros. Admita que o trenó parte do repouso e que o atrito é desprezível.
Questão 27
Um trenó é rebocado por uma pessoa sobre um campo gelado. A pessoa puxa o trenó (massa total de ) com uma força de , fazendo um anglo de com a horizontal. Determine:
- A velocidade do trenó depois de cobrir cinco metros. Admita que o trenó parte do repouso e que o atrito é desprezível.
Questão 28
Um bloco de massa se move em uma linha reta sobre uma superfície horizontal sem atrito sob a influência de uma força que varia com a posição, como mostra a Fig. 1. A escala vertical do gráfico é definida por . Qual é o trabalho realizado pela força enquanto o bloco se desloca da origem até ?
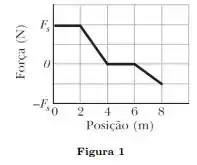
Questão 29
Um bloco de parte do repouso sobre um plano inclinado rugoso que faz um ângulo de com a horizontal. O coeficiente de atrito cinético entre o bloco e o plano é . Quando o bloco desce ao longo do plano, a energia mecânica do sistema Terra-bloco:
Dado: (capa da prova)
(A) aumenta de ;
(B) diminui de ;
(C) não se altera
(D) diminui de ;
(E) aumenta de ;
Ver solução completaQuestão 30
Um bloco de massa está sendo puxado ao longo de uma superfície com atrito. Se é a força externa que puxa o bloco, a força de atrito, a força peso, a força normal e a força resultante, todas elas atuando sobre o corpo, o trabalho de cada uma dessas forças, após o bloco deslocar-se por 2 metros a velocidade constante vale, respectivamente:
(A) , , , , ;
(B) , , , , ;
(C) , , , , ;
(D) , , , , ;
(E) , , , , ;
Ver solução completaQuestão 31
Um trenó e seu ocupante, com uma massa total de , descem uma encosta e atingem
um trecho horizontal retilíneo com uma velocidade inicial de . Se uma força desacelera o trenó até o repouso a uma taxa constante de
c) Qual o trabalho realizado pela força sobre o trenó?
Ver solução completaQuestão 32
Uma força age sobre uma partícula enquanto a partícula se desloca ao longo de um eixo com em newtons, em metros e uma constante. Em , a energia cinética da partícula é , em , é . Determine o valor de .
Ver solução completaQuestão 33
Um galão de azeite de se move ao longo do eixo de acordo com a equação , com em metros e em segundos, impulsionado por uma força . Determine
O trabalho realizado por entre os instantes e s.
Ver solução completaQuestão 34
Um bloco de gelo escorrega para baixo em uma rampa sem atrito com inclinação de enquanto um operário o puxa (através de uma corda) com uma força paralela à rampa. Quando o bloco desliza uma distância ao longo da rampa, sua energia cinética aumenta de . Quão maior seria a energia cinética se o bloco não estivesse sendo puxado pela corda?
Ver solução completaQuestão 35
Um objeto preso a um fio ideal descreve uma trajetória circular num plano horizontal com rapidez constante. O trabalho realizado pela tensão é nulo porque
(A) O deslocamento para cada revolução é nulo.
(B) A tensão média para cada revolução é nula.
(C) A velocidade é constante.
(D) A magnitude da aceleração é nula.
(E) A tensão é perpendicular a cada deslocamento infinitesimal.
Ver solução completaQuestão 36
“Caminhando contra o vento
Sem lenço e sem documento
No sol de quase dezembro
Eu vou...”
Trecho da música “Alegria, Alegria” de Caetano Veloso que concorreu no III Festival da Record, em 1967 - um ícone do movimento Tropicalista.
Imaginemos o homem da canção com massa de e caminhando na direção de uma força de , a força do vento é de , o coeficiente de atrito é de . Os Trabalhos realizados por todas as forças que agem sobre o homem quando ele se descola em , são:
(a) e .
(b) e
(c) e .
(d) e .
(e) e .
Ver solução completaQuestão 37
“Caminhando contra o vento
Sem lenço e sem documento
No sol de quase dezembro
Eu vou...”
Trecho da música “Alegria, Alegria” de Caetano Veloso que concorreu no III Festival da Record, em 1967 - um ícone do movimento Tropicalista.
Imaginemos o homem da canção com massa de e caminhando na direção de uma força de , a força do vento é de , o coeficiente de atrito é de . Os Trabalhos realizados por todas as forças que agem sobre o homem quando ele se descola em , são:
(a) e .
(b) e
(c) e .
(d) e .
(e) e .
Ver solução completaQuestão 38
Bia está puxando sua mochila de rodinhas (sem atrito) para ir para a escola. Num determinado trecho, ela sobe uma rua com inclinação de graus aplicando uma força de . Nesse trecho, ela percorre uma trajetória cuja componente horizontal é de . Determine a componente horizontal do trabalho (em Joules) realizado sobre a mochila.
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 39
Um guindaste ergue verticalmente um caixote a uma altura de em . Um segundo guindaste ergue o mesmo caixote à mesma altura em . Em ambos os casos o içamento foi feito com velocidade constante. O trabalho realizado pelo primeiro guindaste, comparado com o trabalho realizado pelo segundo, é
(a) quatro vezes maior
(b) igual à metade.
(c) duas vezes maior.
(d) o mesmo
(e) quatro vezes menos
Ver solução completaQuestão 40
Um objeto de desloca-se numa trajetória retilínea de acordo com a equação horária dos espaços , onde é medido em metros e em segundos. Calcule o trabalho realizado pela força resultante que atua sobre o objeto durante um deslocamento de .
(a)
(b) .
(c)
(d)
(e)
Ver solução completaQuestão 41
Um bloco move-se com velocidade de módulo constante sobre uma superfície plana e horizontal. Sobre ele atuam a força peso, as forças normal e de atrito devidas ao contato do bloco com a superfície e uma força que o empurra. O trabalho realizado pela força resultante sobre o bloco após ele realizar um deslocamento no plano é
(a) positivo;
(b) negativo;
(c) não é possível determiná-lo sem conhecer o módulo da força de atrito;
(d) não é possível determiná-lo sem conhecer a sua trajetória;
(e) nulo;
Ver solução completaQuestão 42
Uma bola é obrigada a seguir uma trajetória circular devido a uma força conservativa. Durante um intervalo de tempo , a bola realiza exatamente uma revolução. Qual das seguintes afirmações sobre o trabalho durante o tempo é verdadeira?
A. O trabalho é maior do que zero;
B. O trabalho depende apenas do raio da circunferência;
C. O trabalho depende apenas da velocidade da bola;
D. O trabalho depende apenas do tempo;
E. O trabalho é igual a zero;
Ver solução completaQuestão 43
Questão 1). Um corpo de massa é arrastado horizontalmente para a direita por uma força constante , que faz um ângulo acima da superfície . O corpo parte do repouso e após percorrer uma distância , o módulo de sua velocidade é . Há atrito entre o corpo e a superfície. Considere a aceleração da gravidade local. Com base nos conceitos de Energia e Trabalho (conteúdos estudados nos cap. 4, 5 e 6), determine, em função dos dados que se fizerem necessários (, , , , e )
a) o trabalho realizado sobre o corpo pela força .
b) o trabalho total realizado sobre o corpo.
c) o trabalho realizado sobre o corpo pela força de atrito cinético.
d) o coeficiente de atrito cinético entre o corpo e a superfície.
Ver solução completaQuestão 44
8. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
a)
Ver solução completaQuestão 45
8. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
c)
Ver solução completaQuestão 46
8. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
b)
Ver solução completaQuestão 47
10. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
a)
Ver solução completaQuestão 48
10. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
b)
Ver solução completaQuestão 49
10. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
c)
Ver solução completaQuestão 50
10. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
d)
Ver solução completaQuestão 51
10. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
e)
Ver solução completaQuestão 52
10. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
f)
Ver solução completaQuestão 53
13. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
a)
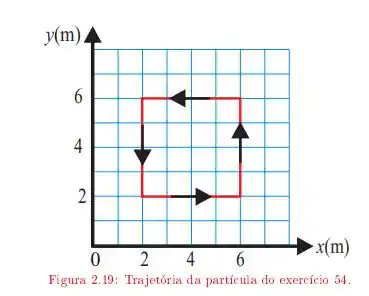
Ver solução completaQuestão 54
13. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
b)
Ver solução completaQuestão 55
13. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
c)
Ver solução completaQuestão 56
13. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
d)
Ver solução completaQuestão 57
13. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
e)
Ver solução completaQuestão 58
No instante uma partícula inicia seu movimento ao longo do eixo . Sua energia cinética cresce linearmente com o tempo , a força resultante que age sobre a partícula deve ser:
(a) proporcional a .
(b) constante.
(c) proporcional a .
(d) inversamente proporcional a .
(e) proporcional a .
Ver solução completaQuestão 59
Preencha os campos com a sua resposta.
Uma força atua sobre uma partícula cuja trajetória é dada por:
Onde o tempo é dado em segundos.
O trabalho realizado pela forma sobre a partícula no intervalo de tempo entre e é igual a ____ , enquanto a potência aplicacda ao bloco em é igual a ____ .
Ver solução completaQuestão 60
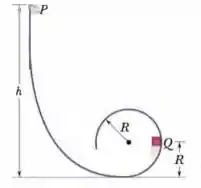
Na figura, um pequeno bloco de massa pode deslizar em uma pista sem atrito que forma um loop de raio . O bloco é liberado a partir do repouso no ponto , a uma altura acima do ponto mais baixo do loop. Qual é o trabalho realizado sobre o bloco pela força gravitacional quando o bloco se desloca do ponto para
(a) o ponto e
(b) o topo do loop?
Se a energia potencial gravitacional do sistema bloco-Terra é tomada como zero no ponto mais baixo do loop, qual é a energia potencial quando o bloco se encontra
(c) no ponto ,
(d) no ponto e
(e) no topo do loop? Se, em vez de ser simplesmente liberado, o bloco recebe uma velocidade inicial para baixo ao longo da pista, as respostas dos itens de (a) e (e) aumentam, diminuem ou permanecem as mesmas?
Quais são os módulos das componentes
(f) horizontal
(g) vertical da força resultante que atua sobre o bloco no ponto Q?
(h) Para que valor de deveria o bloco ser solto, a partir do repouso, de modo que ele fique na iminência de perder contato com a superfície no topo do loop?
Questão 61
1. Um caminhão de três toneladas está sendo embarcado num navio por um guindaste que exerce uma força de , para cima, sobre o veículo. Esta força, suficiente para provocar o início da subida do caminhão, atua sobre uma distância de dois metros. Calcule
(a) o trabalho efetuado pelo guindaste neste deslocamento.
Ver solução completaQuestão 62
O Trabalho realizado por uma força constante é positivo se:
a componente da força na direção e sentido do deslocamento é positiva.
o ângulo entre a força e o deslocamento é maior que .
o produto escalar entre a força e o deslocamento é negativo.
o ângulo entre a força e o deslocamento é maior que .
a componente da força na direção e sentido do deslocamento é negativa.
Ver solução completaQuestão 63
Uma partícula move-se no plano em uma trajetória retilínea ao longo do eixo , da origem ao ponto , e a seguir ao longo de uma trajetória retilinea do ponto ao ponto , como inficado na figura. Durante todo o percurso agem sobre a partícula três forças constantes , e de mesmo módulo. Os ângulos que as forças , e fazem com o eixo são, respectivamente, , e . Denotando os respectivos trabalhos das três forças em todo o percurso de a por , e , podemos afirmar que
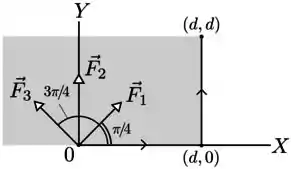
- , e ;
- , e ;
- , e ;
- , e ;
- O trabalho realizado por cada uma das três forças é o mesmo.
Questão 64
Em um certo instante, um objeto que se comporta como uma partícula sofre a ação de uma força quando sua velocidade é . Qual é a taxa instantânea com a qual a força realiza trabalho sobre o objeto? Em outro instante, a velocidade tem apenas a componente . Se a força não muda e a potência instantânea é , qual é a velocidade do objeto nesse instante?
Ver solução completaQuestão 65
A personagem das tirinhas de Maurício de Souza, Mônica, é lembrada por sua grande força muscular. Imaginemos, que ela, aplique uma força, que faça com que seus amigos Xaveco, Cascão e Cebolinha que estavam sentados em um balanço, sejam arremessados do balanço com uma grande velocidade. Essa situação está associada à:
(a) Energia Cinética e Energia Potencial.
(b) Trabalho e Energia Cinética.
(c) Transformação de Energia.
(d) Conservação de Energia.
(e) Trabalho e Energia Potencial.
Ver solução completaQuestão 66
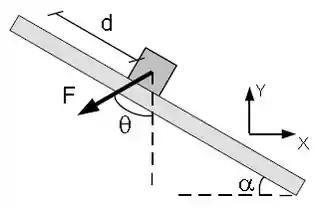
Um bloco de massa é deslocado para cima por uma força uma distância ao longo de um plano inclinado. O plano está inclinado de em relação à horizontal, e a força faz um ângulo com a vertical. Determine o trabalho realizado pela força ao longo do deslocamento. Utilize o sistema de coordenadas indicado na figura.
Questão 68
Um carro de massa está se movendo em linha reta com uma velocidade . O carro freia, travando os pneus, e desliza até parar. Qual das seguintes forças realiza um trabalho diferente de zero?
a) Normal
b) Gravitacional
c) Atrito cinético
d) Atrito estático
e) Força centrípeta
Ver solução completaQuestão 69
Um bloco é puxado por uma distância horizontal ao longo de uma superfície com atrito por uma força constante que faz um ângulo com a horizontal, conforme a figura abaixo. Sabe-se que o módulo da força aplicada é . Considere que o bloco não perde contato com a superfície em nenhum momento.
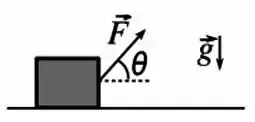
(a) Determine o trabalho realizado pela força quando .
(b) Calcule o trabalho realizado pela força quando .
(c) Qual é o trabalho realizado pela força peso quando ? Justifique.
Ver solução completaQuestão 70
Uma partícula de massa move-se ao longo do eixo horizontal sujeita à ação de uma única força , com em metros e em newtons. Inicialmente a partícula encontra-se na posição com velocidade inicial . Qual é a velocidade ao passar pela posição ?
Questão 71
Um funcionário empurra, num assoalho áspero, uma escrivaninha, cuja massa é igual a , com velocidade constante, por uma distância de . O coeficiente de atrito entre a mesa e o assoalho é de .
a. Qual o trabalho realizado pelo funcionário sobre a escrivaninha?
Ver solução completaQuestão 72
Um funcionário empurra, num assoalho áspero, uma escrivaninha, cuja massa é igual a , com velocidade constante, por uma distância de . O coeficiente de atrito entre a mesa e o assoalho é de .
b. Qual o trabalho realizado pela força peso, pela força normal e pela força de atrito?
Ver solução completaQuestão 73
Um funcionário empurra, num assoalho áspero, uma escrivaninha, cuja massa é igual a , com velocidade constante, por uma distância de . O coeficiente de atrito entre a mesa e o assoalho é de .
c. Qual o trabalho realizado sobre a escrivaninha por todas as forças que atuam sobre ela?
Ver solução completaQuestão 74
Um bloco de está apoiado sobre uma mesa e ligado a uma mola horizontal que obedece a lei de Hooke , onde se mede a partir do comprimento de equilíbrio da mola e a constante de força vale . A mola está comprimida até .
b) Determinar a velocidade escalar do bloco em , admitindo que não haja atrito entre o bloco e a mesa;
Ver solução completaQuestão 75
Um engradado de massa é puxado com velocidade constante por um guincho, numa distância , numa rampa sem atrito, até uma altura acima do ponto de partida.
b. Quanto trabalho seria necessário para elevar o engradado verticalmente para cima, na mesma altura H? Neste caso, qual a força exercida pelo guincho?
Ver solução completaQuestão 76
Um engradado de massa é puxado com velocidade constante por um guincho, numa distância , numa rampa sem atrito, até uma altura acima do ponto de partida.
c. Compare e analise os resultados encontrados nos itens anteriores.
Ver solução completaQuestão 77
Um corpo de está em repouso sobre uma superfície horizontal, sem atrito. Uma força de módulo constante de , fazendo um ângulo de 30◦ com a horizontal, puxa o corpo. Determinar o trabalho efetuado pela força da corda e a velocidade escalar final do corpo, depois de deslocar-se sobre a superfície horizontal.
Ver solução completaQuestão 78
Um bloco de está apoiado sobre uma mesa e ligado a uma mola horizontal que obedece a lei de Hooke , onde se mede a partir do comprimento de equilíbrio da mola e a constante de força vale . A mola está comprimida até .
a) Determinar o trabalho efetuado pela mola quando o bloco se desloca desde até a sua posição de equilíbrio , admitindo que não haja atrito entre o bloco e a mesa;
Ver solução completaQuestão 79
Um bloco de está apoiado sobre uma mesa e ligado a uma mola horizontal que obedece a lei de Hooke , onde se mede a partir do comprimento de equilíbrio da mola e a constante de força vale . A mola está comprimida até .
c) Determinar a velocidade escalar do bloco quando a mola está na posição de equilíbrio, mas agora admitindo que o coeficiente de atrito cinético entre a mesa e o bloco é .
Ver solução completaQuestão 80
Garfield,o gordo gato das Tirinhas de David, J, parte do escorrega com uma velocidade , ao final da sua descida depara-se com uma árvore e, então, assume a velocidade de . A distância entre o escorrega e a árvore é e o Peso do gordo gato é de A força com que Garfield se chocou com a árvore, foi:
OBS: Lembrando as equações: , onde é a força resultante do sistema, é o ângulo entre a força e o deslocamento sofrido e é o deslocamento. , onde é a massa do corpo e é a velocidade do corpo.
(a) na direção contrária ao Garfield.
(b) na direção contrária ao Garfield.
(c) na direção contrária ao Garfield.
(d) na direção contrária ao Garfield.
(e) na direção contrária ao Garfield.
Ver solução completaQuestão 81
(Capítulo 7 – Problemas Adicionais – Exercício 55) Qual é o trabalho realizado por uma força , com em metros, ao deslocar uma partícula de uma posição para uma posição ?
Ver solução completaQuestão 82
(Capítulo 7 – Problemas Adicionais - Exercício 56) Para puxar um engradado de sobre um piso horizontal sem atrito, um operário aplica uma força de que faz um ângulo de para cima com a horizontal. Em um deslocamento de , qual é o trabalho realizado sobre o engradado (a) pela força do operário, (b) pela força gravitacional e (c) pela força normal do piso? (d) Qual é o trabalho total realizado sobre o engradado?
Ver solução completaQuestão 83
Uma partícula move-se, sob a ação da força , no plano . Calcule:
a) O trabalho realizado pela força ao longo do quadrado indicado na figura . O que você conclui sobre o caráter conservativo ou não de ?
Ver solução completaQuestão 84
Uma partícula de massa move-se ao longo do eixo sob a ação de uma força conservativa em uma região onde a energia potencial varia conforme o gráfico apresentado na figura .
d) Determine o trabalho realizado pela força para deslocar o corpo desde até ;
Ver solução completaQuestão 85
Uma corda é usada para puxar um bloco de com velocidade constante por ao longo de um piso horizontal. A força que a corda exerce sobre o bloco é de , dirigida acima da horizontal. Quais são
(a) o trabalho realizado pela força da corda,
(b) o aumento na energia térmica do sistema bloco-piso e
(c) o coeficiente de atrito cinético entre o bloco e o piso?
Ver solução completaQuestão 86
Considerando o trabalho realizado por uma força , entre a origem e o ponto ao longo dos caminhos:
- Primeiro ao longe de e depois ao longo de
- Primeiro ao longo de e depois ao longo de
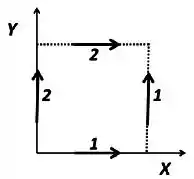
Podemos afirmar que:
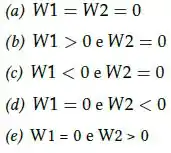
Questão 87
A posição de uma partícula de massa é dada pela expressão onde é dado em metros e em segundos. Obtenha o trabalho realizado, durante os primeiros , pela força que atua sobre a partícula.
Ver solução completaQuestão 88
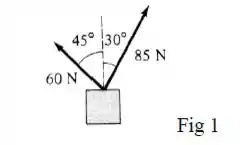
A Figura 1 mostra duas forças puxando uma caixa ao longo do chão:
(a) Quanto trabalho cada força faz quando a caixa é deslocada na vertical?
(b) Qual é o trabalho total realizado pelas duas forças para puxar a caixa nesta distância?
Questão 89
A Figura 1 mostra duas forças puxando uma caixa ao longo do chão:
(a) Quanto trabalho cada força faz quando a caixa é deslocada na vertical?
(b) Qual é o trabalho total realizado pelas duas forças para puxar a caixa nesta distância?
Questão 90
Uma caixa de massa igual a desliza por um plano com inclinação de A aceleração da caixa é de e o plano inclinado tem de comprimento.
(a) Qual é a energia cinética da caixa quando ela atinge a base do plano inclinado?
(b) Quanto trabalho é gasto para superar o atrito?
(c) Qual é a magnitude da força de atrito que atua na caixa conforme ela desliza pelo plano inclinado?
Ver solução completaQuestão 91
Um disco horizontal gira em torno de um eixo vertical que passa pelo seu centro, com velocidade angular constante. Coloca-se um corpo de pequenas dimensões e massa sobre o disco a uma distância de do seu centro. Verifica-se que o atrito entre o corpo e a superfície do disco é suficiente para que ele permaneça na mesma posição do disco em que foi colocado. Ou seja, ele não desliza sobre o disco. O disco dá uma volta completa no intervalo de tempo . Sabendo-se que o coeficiente de atrito estático entre o corpo e a mesa é , o trabalho realizado pela força de atrito numa volta completa é igual a:
Questão 92
Um bloco de massa m desce de uma distância d ao longo de uma superfície plana inclinada, fixa ao solo, que faz um ângulo θ com a horizontal. O coeficiente de atrito cinético entre o bloco e a superfície vale μ. Os trabalhos realizados pelas forças gravitacional (), normal () e força de atrito () valem, respectivamente:
a)
b)
c)
d)
e)
Ver solução completaQuestão 93
Um bloco desce um plano inclinado com velocidade constante. Atuam sobre o bloco, além da força peso, apenas as forças normal e de atrito devidas ao contato entre o bloco e a superfície do plano. Em um deslocamento que o bloco realiza sobre o plano, pode-se afirmar que:
(a) O trabalho realizado pela força de atrito é positivo.
(b) O trabalho realizado pela força peso é negativo.
(c) O trabalho realizado pela força resultante sobre o bloco é positivo.
(d) O trabalho realizado pela força resultante sobre o bloco é nulo.
(e) O trabalho realizado pela força normal é negativo.
Ver solução completaQuestão 94
Uma caixa se move 10 m para a direita quando uma mulher a puxa com uma força de 10N. Classifique as situações mostradas na figura de acordo com o trabalho realizado por sua força, do menor para o maior.
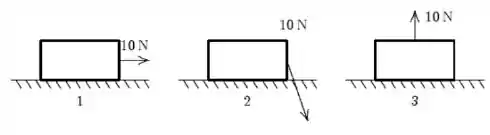
a) 1, 2, 3
b) 2, 1, 3
c) 2, 3, 1
d) 1, 3, 2
e) 3, 2, 1
Ver solução completaQuestão 95
A força de módulo atua sobre um objeto formando um ângulo constante de com a direção do deslocamento do objeto. Se o deslocamento é de , o trabalho realizado pela força, em joules, é igual a: (Dado: )
- 100
- 150
- 125
- 260
- 300
Questão 96
Se uma força é sempre perpendicular à direção do movimento de um objeto, essa força não muda a energia cinética do objeto. Sobre esta afirmação, é correto dizer que:
(a) A afirmação é sempre falsa
(b) A afirmação é sempre verdadeira
(c) A afirmação é verdadeira somente quando a força é conservativa
(d) A afirmação é falsa quando a força não é conservativa
(e) A afirmação é verdadeira somente se o objeto percorre uma curva fechada
Ver solução completaQuestão 97
19) Uma roda de , essencialmente um aro fino com de raio, está girando a . Ela precisa ser parada em . (a) Qual é o trabalho necessário para fazê-la parar?
Ver solução completaQuestão 98
O trabalho mecânico realiza-se por intermédio de uma força, caracterizado pelo deslocamento provocado pela força no corpo. Sua unidade, o Joule . Calcula-se o trabalho mecânico através do produto da intensidade da força pelo deslocamento provocado. Com uma força de e deslocamento provocado de , o trabalho mecânico seria:
- Nda
Questão 99
Na figura, um bloco de gelo escorrega para baixo em uma rampa sem atrito com uma inclinação enquanto um operário puxa o bloco (através de uma corda) com uma força, que tem um módulo de e aponta para cima ao longo da rampa. Quando o bloco desliza uma distância ao longo da rampa, sua energia cinética aumenta . Quão maior seria a energia cinética se o bloco não estivesse sendo puxado por uma corda?
Questão 100
Um esquiador é puxado por uma corda para o alto de uma encosta que faz um ângulo de com a horizontal. A corda se move paralelamente à encosta com uma velocidade constante de . A força da corda realiza de trabalho sobre o esquiador quando este percorre uma distância de encosta acima.
(a) Se a velocidade constante da corda fosse , que trabalho a força da corda teria realizado sobre o esquiador para o mesmo deslocamento? A que taxa a força da corda realiza trabalho sobre o esquiador quando a corda se desloca com uma velocidade de
(b)e
(c) ?
Ver solução completaQuestão 101
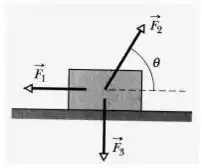
A figura mostra três forças aplicadas a um baú que se desloca para a esquerda sobre um piso sem atrito. Os módulos das forças são , e ; o ângulo indicado é . No deslocamento,
(a) qual é o trabalho total realizado sobre o baú pelas três forças e
(b) a energia cinética do baú aumenta ou diminui?
Questão 102
Um bloco desce um plano inclinado com velocidade constante. Atuam sobre o bloco, além da força peso, apenas as forças normal e de atrito devidas ao contato entre o bloco e a superfície do plano. Considere as seguintes afirmativas:
I – O trabalho realizado pela força resultante sobre o bloco após ele realizar um deslocamento sobre o plano é nulo.
II – O trabalho realizado pela força peso após ele realizar um deslocamento sobre o plano é nulo.
III – O trabalho realizado pela força de atrito após ele realizar um deslocamento sobre o plano é negativo.
Dentre as afirmativas acima estão corretas apenas
a) I e III
b) II
c) I
d) III
e) I e II
f) II e III
g) I, II e III
h) nenhuma está correta
Ver solução completaQuestão 103
Uma partícula se desloca ao longo do eixo sob a ação de uma força cuja componente é dada por:
Onde está em metros. O trabalho realizado pela força quando a partícula se desloca da origem até é igual a:
Ver solução completaQuestão 104
Um pêndulo simples consiste numa massa presa a uma corda de comprimento e de massa desprezível. A massa é solta quando a corda faz um ângulo de com a vertical. Considere os trabalhos realizados pela força peso e pela tensão na corda desde a liberação da massa até o instante em que ela passa pelo ponto mais baixo. Os trabalhos realizados pelo peso () e pela tensão () são, respectivamente
(a) ,
(b) ,
(c) ,
(d) ,
(e) ,
Ver solução completaQuestão 105
Uma bola está inicialmente presa ao teto no interior de um vagão de trem que se move em linha reta na horizontal e com velocidade constante. Em um dado instante, a bola se solta e cai sob a ação da gravidade. Para um observador no interior do vagão, a bola descreve uma trajetória vertical durante a queda, e para um observador parado fora do vagão, a trajetória é um arco de parábola. Assim, o trabalho realizado pela força peso durante a descida da bola é:
- Maior para o observador no vagão
- Diferente de zero e com mesmo valor para ambos os observadores
- Menor para o observador no vagão
- Maior para o observador no solo
- Zero para ambos os observadores
Questão 106
Uma bola de massa m = 0, 5 kg é presa a um pino por um o leve e inextensível de 0, 8 m de comprimento. A bola é abandonada quando está na horizontal. Na parte mais baixa da trajetória a bola atinge um bloco de massa M = 2, 0 kg, inicialmente em repouso sobre uma superfície áspera. A colisão, entre a bola e o bloco, pode ser considerada como perfeitamente elástica. O coeficiente de atrito cinético entre o bloco e a superfície é µc = 0, 16.
a. Qual o trabalho realizado pelas forças que atuam sobre a bola?
Ver solução completaQuestão 107
Uma partícula move-se. sob a ação da força , no plano . Calcule:
O trabalho realizado pela força ao longo da diagonal do quadrado da trajetória da figura , partindo da posição e chegando a posição .
Questão 108
O cabo de um elevador de rompe-se, quando ele está parado no primeiro andar. No instante do rompimento, o piso do elevador encontra-se a uma distância acima de uma mola amortecedora, cuja constante de mola . Um sistema de segurança prende os trilhos laterais que servem de guia, de modo que uma força de atrito constante de opõe-se ao movimento do elevador após o rompimento do cabo. Determine:
A distância total, aproximada, percorrida pelo elevador antes de parar totalmente, utilizando, para isto, o princípio da conservação de energia. Porque esta resposta não é exata?
Ver solução completa