Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 2.9 - Ex. 61

Um gato sonolento observa um vaso de flores que passa por uma janela aberta, primeiro subindo e depois descendo. O vaso permanece à vista por um tempo total de 0,50   s e a altura da janela é 2,00   m . Que distância acima do alto da janela o vaso atinge?

Passo 1

Questão estranha né? Por que um vaso de flores estaria fazendo um movimento de subida e descida assim do nada? O que imaginei foi algo assim

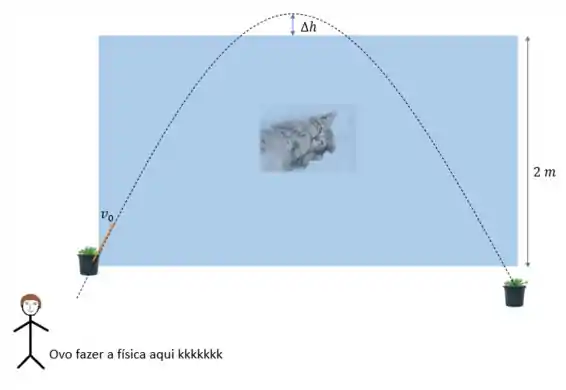
Onde o garoto levado taca o vaso obliquamente (e vai levar esporro da mão por isso) e imagina que o vaso entra na área azul da janela a uma velocidade oblíqua v 0 e sai dela com a mesma velocidade, o tempo que ele fica dentro da área da janela é de 0.5   s .

Dessa forma a equação da posição vertical desse vaso será de:

Δ L = v 0 y t - g 2 t 2

Onde Δ L é a altura da janela e v 0 y é a velocidade projetada na vertical para a velocidade de entrada no vaso na área da janela. Então se substituirmos o que conhecemos nós temos:

2 = v 0 y t - 9.81 2 t 2

Isolando v 0 y teremos:

v 0 y = 2 t + 4.905 t

Passo 2

Por Torricelli temos que:

v f 2 = v 0 2 + 2 a Δ s

Onde no passo mais alto da trajetória a velocidade vertical é nula e no caso da questão Δ s = 2 + Δ h portanto:

0 = 2 t + 4.905 t 2 - 2 ⋅ 9.81 ⋅ 2 + Δ h

E no ponto mais alto da trajetória o tempo de trajetória é o tempo total e como o tempo total de atravessamento da área da janela é de 0.5   s , logo t para que o vaso esteja no ponto mais alto da trajetória será de 0.25   s , logo:

2 ⋅ 9.81 ⋅ 2 + Δ h = 2 0.25 + 4.905 ⋅ 0.25 2

Fazendo essa conta encontramos:

Δ h = 2.34   m

Resposta

a )   Δ h = 2.34   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barata de estalo pode se projetar verticalmente com uma aceleração de cerca de 400g (uma ordem de grandeza maior que a suportável pelos humanos!). Ela salta “desdobrando” suas pernas de 0,60 cm de c
Em t = 0 , uma pedra é largada do topo de um penhasco, acima de um lago. Outra pedra é atirada para baixo, 1,6 s após, do mesmo ponto e com uma rapidez inicial de 32 m/s. As duas pedras atingem a água
Duas pedras são largadas da beira de um precipício de 60 m, a segunda pedra 1,6 s após a primeira. A que distância abaixo do topo do precipício está a segunda pedra quando a separação entre as duas pe
Uma professora de física, equipada com um foguete-mochila, abandona um helicóptero a uma altitude de 575 m com velocidade inicial zero. (Despreze a resistência do ar.) Durante 8,0 s ela cai livremente
Resolva o problema 96 se a colisão ocorre quando as bolas se deslocam no mesmo sentido e a rapidez de A é 4 vezes a de B.