Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 33.1 - Ex. 38
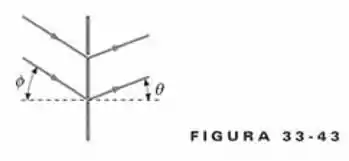
Luz incide formando um ângulo com a normal em um plano vertical que contém duas fendas de separação (Figura 33-43). Mostre que os máximos de interferência estão localizados em ângulos dados por .
Passo 1
Saaalve rapeize, vamo de questão? Então, nela a gente vai considerar a separação das fendas como . Podemos encontrar a diferença total do caminho quando a luz incide em um ângulo e definir esse resultado igual a um múltiplo inteiro do comprimento de onda da luz para obter a equação dada. Feshow? Pois bora!
Passo 2
Expressando a diferença total, temos:
A condição para a interferência construtiva:
Onde é um inteiro.
Passo 3
Para finalizar, substituiremos:
Agora dividiremos os dois lados por , para a gente provar o que a questão pede:
Resposta
Ei, a resposta está no passo a passo :)