Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 32.1 - Ex. 57
No método de Bessel para determinar a distância focal de uma lente, um objeto e um anteparo estão separados por uma distância , onde . É, então, possível, colocar uma lente entre o objeto e o anteparo em duas posições diferentes permitindo que exista uma imagem do objeto no anteparo, em um dos casos ampliada, e no outro, reduzida. Mostre que, se a distância entre duas posições da lente é , então a distância focal é dada por . Dica: Veja a figura 32-60.
Passo 1
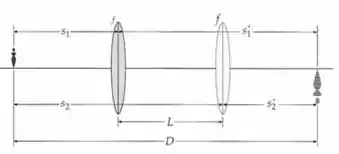
Bom dia, boa tarde, boa noite, boa madrugada, TUDO BEM CONTIGO? Espero que sim, simbora resolver mais um problema. Bem, o diagrama de raios mostra a posição das duas lentes e da imagem correspondente e as distâncias dos objetos (representados pelo numeral 1 e 2). Nós podemos usar a equação das lentes delgadas para relacionar os dois conjuntos de imagem e distância objeto à distância focal da lente e, em seguida usar a figura para expressão as relações entre essas distâncias e as distâncias e para eliminar , , e e obter uma expressão relacionando , e .Dito isto, vamos resolver esse problema!
Passo 2
Primeiro, vamos relacionar as distâncias do objeto e da imagem para a posição das duas lentes à distância focal das lentes:
e
Resolveremos para , assim temos:
(1)
As distâncias e podem ser expressas em termos de distância imagem e objeto:
Substituindo as somas na equação (1), obtemos:
A partir da figura, temos que e , então temos , logo:
Aplicando o produto entre e , obtemos:
(2)
Da equação das lentes delgadas, temos que:
Agora, substituindo na equação (2), temos:
PRONTO, temos tudo o que a questão pediu, MENOS UMA, é tudo por hoje, bons estudos e fica bem ;)
Resposta
Ei, a resposta está no passo a passo :)