Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 55

Os navios A e B deixam o porto simultaneamente. Nas próximas duas horas, o navio A navega a 20 mph para 30° a oeste do norte, enquanto o navio B navega para 20° a leste do norte a 25 mph.

  1. Qual é a distância entre os dois navios duas horas após suas partidas?

  2. Qual é o módulo da velocidade do navio A do ponto de vista do navio B?

Passo 1

Seguindo uma roda dos ventos simplificada com as direções norte (N), sul (S), leste (L) e oeste (O) podemos esquematizar os vetores

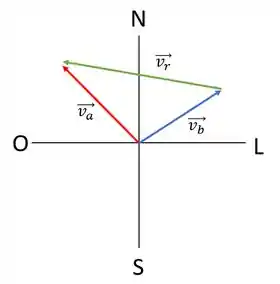
Em que v a → é o navio A, v b →   é o navio B e que v r →   é o vetor resultante das velocidades dos navios A e B. Podemos escrever como

v r → = v a → + v b →

E sabemos que A

v = 20   m p h

θ = 30 °

E B é

v = 25   m p h

θ = 20 °

Passo 2

  1. A velocidade vetorial dos dois navios pode ser escrita como

    2. v x = v 0 cos ⁡ θ

    v y = v 0 s e n   θ

    Assim se juntarmos

    v → = v 0 cos ⁡ θ î   + v 0   s e n   θ j

    Mas como v 0 é igual para ambos, podemos escrever

    v → = v 0   ( cos ⁡ θ î + s e n   θ   j )

    Então para o navio A e B vão ter a seguinte cara

    v A → = 20   cos ⁡ 30 ° î - s e n   30 °   j = 17,32   î - 10 j   m p h

    v B → = 25   cos ⁡ 20 ° î + s e n   20 °   j = 23,49   î + 8,55 j   m p h

    Em v A →   o seno é negativo por questão trigonométrica, ele está no segundo quadrante, assim pegamos seu oposto por esse motivo. Para descobrir a distância (r) faremos

    r → = v → Δ t

    Substituindo para o navio A e B, temos

    r A → = 2   .   v A → = 34,64   î - 20 j   m i l h a s

    r B → = 2   .   v B → = 26,98   î + 17,10 j   m i l h a s

    E o módulo da distância vai ser (  r r → )

    r r → = r A → + r B → = 34,64 - 26,98 î - 20 - 17,1 j =

    = - 12,34 2 + - 37,1 2 = r r → = 39,1   m i l h a s

    Passo 3

  2. Como já temos as velocidades vetoriais

v A → = 17,32   î - 10 j   m p h

v B → = 23,49   î + 8,55 j   m p h

Assim

v r → = v a → + v B → = 17,32 - 2 3,49 î - ( - 10 + 8,55 ) j =

= - 6,17 2 + - 18,55 2 = v r → = 19,5   m p h

Resposta

  1. 39,1   m i l h a s
  2. 19,5   m p h
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um projétil, disparado com velocidade inicial desconhecida, cai 20,0 s depois no lado de um morro, a uma distância horizontal de 3000 m do ponto inicial e 450 m acima deste ponto. (ignore a resistênci
Você assite seu amigo jogando hóquei. Durante o jogo, ele atinge o disco de tal forma que, ao chegar no seu ponto mais alto, o disco passa de raspão por cima do muro de acrílico de 2,80 m de altura qu
Consertando o telhado de sua casa, você deixa o martelo cair acidentalmente. O martelo escorrega pelo telhado a uma rapidez constante de 4,0 m/s. O telhado faz ângulo de 30° com a horizontal e seu pon
Uma bola de squash tipicamente rebate de uma superfície voltando com 25 por cento da rapidez que tinha ao atingir a superfície. Seja uma bola de squash lançada em uma trajetória baixa, a uma altura de
Carlos está pedalando, aproximando-se de um riacho de 7,0 m de largura. Uma rampa inclinada de 10° foi construída para aqueles corajosos que queiram tentar atravessar o riacho. Carlos desenvolve a máx