Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 3- Ed: 6º - Capítulo 35.1 - Ex. 13

Uma partícula que tem massa m está viajando na direção do aumento de x. A energia potencial da partícula é igual a zero em toda a região x 0, onde U0> 0. (a) Mostre que se a energia total é E = αU0, onde α ≥ 1, o número da onda k2 na região x> 0 é dado por k2 = k1 (α - 1) α, onde k1 é o número da onda na região x

Passo 1

(a) Usando a conservação de energia, a energia total da partícula deve ser igual a:

α U 0 = ℏ 2 k 2 2 2 m + U 0

Isolando k 2 :

ℏ 2 k 2 2 2 m = α U 0 - U 0 = U 0 α - 1

k 2 2 = 2 m U 0 α - 1 ℏ 2

k 2 = 2 m U 0 α - 1 ℏ 2

k 2 = 2 m U 0 α - 1 ℏ

Para k 1 :

α U 0 = ℏ 2 k 1 2 2 m

∴

k 1 = 2 m α U 0 ℏ

Então:

k 2 k 1 = 2 m U 0 α - 1 ℏ 2 m α U 0 ℏ = 2 m U 0 α - 1 2 m α U 0

k 2 k 1 = 2 m U 0 α - 1 2 m α U 0

k 2 k 1 = α - 1 α

∴

k 2 = k 1 α - 1 α

Passo 2

(b) O coeficiente de reflexão é:

R = k 1 - k 2 2 k 1 + k 2 2

Arrumando:

R = k 1 2 1 - k 2 k 1 2 k 1 2 1 + k 2 k 1 2

R = 1 - k 2 k 1 2 1 + k 2 k 1 2

Como vimos no passo anterior:

R = 1 - α - 1 α 1 + α - 1 α 2

Passo 3

Assim, como o coeficiente de transmissão é:

T = 1 - R

Temos:

T = 1 - 1 - α - 1 α 1 + α - 1 α 2

Passo 4

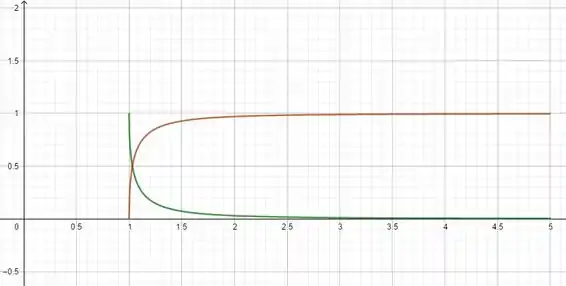
Um gráfico para T (em marrom) e R (em verde) é:

Resposta

(a) k 2 = k 1 α - 1 α

(b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma barreira de energia potencial como a da Fig. 38-15 cuja altura U b é 6,0e V e cuja largura L é 0,70n m . Qual é a energia de elétrons incidentes para os quais o coeficiente de transmissã
(a) Um feixe de prótons de 5,0e V incide em uma barreira de energia potencial de 6,0e V de altura e 0,70n m de largura, a uma taxa correspondente a uma corrente de 1000A . Quanto tempo é preciso esper
Um feixe de elétrons de energia E = 5,1e V incide em uma barreira de altura U b = 6,8e V e largura L = 750p m . Qual é a variação percentual do coeficiente de transmissão T correspondente a uma variaç
Prótons de 3,0M e V incidem em uma barreira de energia potencial de 10f m de espessura e 10M e V de altura. Determine (a) o coeficiente de transmissão T , (b) a energia cinética K t dos prótons que at
Exercício de Livro