Quatro tijolos iguais e homogêneos, de comprimento L, são empilhados de duas formas diferentes em uma mesa, como mostra a Fig. 12-81 (compare com o problema 63). Estamos interessados em maximizar a distância h das duas configurações. Determine as distâncias ótimas , , e e calcule h para os dois arranjos.
Passo 1
Este problema é um pouco mais complicado que o 63, mas também não é difícil. Vamos lá! Primeiro, vamos considerar o sistema de referência ma quina da mesa. Depois vamos ter que aplicar somatório dos momentos pra tentar descobrir os valores máximos de, , e . Vamos começar pela letra (a).
Analisando a situação da segunda fileira de blocos, é trivial que . Se for menor ou maior que isso, o sistema não fica em equilíbrio. Maravilha. Sabendo disso, a gente pode calcular o valor de que faça com que o centro de massa do sistema fique em na quina da mesa (iminência para o sistema cair). Então:
Resolvendo esta equação, a gente descobre que . Logo, .
Passo 2
Na letra (b), a gente tem que reparar que o livro do topo exerce uma força nos dois livros da segunda camada. Isso faz com que possa ser maior que . O esquema abaixo ilustra um pouco disso
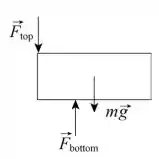
Vale perceber que, pela simetria do problema, . Assim, fazendo um balanço dos momentos, a gente consegue descobrir o valor de .
Por simetria, a gente conclui que . Logo,
Resposta
(a)
(b)