Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 31.1 - Ex. 75
Um raio de luz inicia no ponto , incide em um espelho no plano em algum ponto e reflete através do ponto . (a) Determine o valor de que torna mínima a distância total percorrida pelo raio. (b) Qual é o ângulo de incidência no plano de reflexão? (c) Qual é o ângulo de reflexão?
Passo 1
Faaaaaaaala meu caro, tudo certinho?
A figura aqui embaixo mostra os dois pontos e a superfície refletora. As coordenadas e estão em metros.
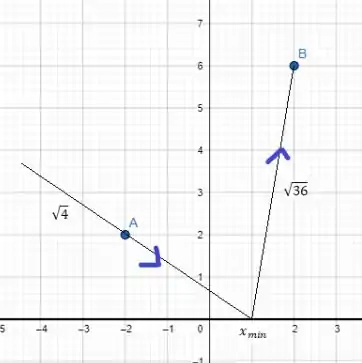
Esse gráfico foi construído pensando nos conjuntos de pontos raio que sai em A, passa por e atinge B. A distância desses pontos pode ser calculada por , mas nesse caso é nulo (nenhum ponto passa por ele).
Expresse a distância total percorrida pela luz:
Podemos escrever e como:
Podemos escrever uma expressão para a distância total percorrida pela luz como uma função de e definir a derivada dessa expressão igual a zero para encontrar o valor de que minimiza a distância percorrida pela luz.
Diferencie em relação a :
Definir esta expressão igual a zero para valores extremos resulta em:
Resolva para para obter:
Passo 2
(b) Supondo que as coordenadas do ponto em que o raio se origina sejam e as coordenadas do ponto terminal sejam a tangente do ângulo de incidência é dada por:
Onde teremos: :
Passo 3
(c) Supondo que as coordenadas do ponto em que o raio se origina sejam e as coordenadas do ponto terminal sejam , a tangente do ângulo de reflexão é dada por:
Onde teremos: :