Um satélite é colocado em uma órbita elíptica cujo ponto mais distante está a da superfície da Terra e cujo ponto mais próximo está a da superfície. Calcule (a) o semi-eixo maior e (b) a excentricidade da órbita
Passo 1
Show de belezeras pessoal, temos o seguinte desenho da situação:
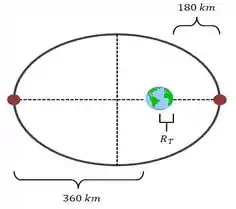
Veja que na figura a Terra foi colocada mais ou menos no foco da elipse, respeitando a 1ª lei de Kepler. Nesse caso, temos a distância do foco (Terra) até a órbita mais próxima, de , enquanto temos a distância do foco (Terra) até a órbita mais distante dada como , além disso, temos que o raio da Terra é . Sabendo disso, bora lá ver como vai ficar essa brincadeira!

Passo 2
A questão fala nos pontos mais/menos próximos da órbita, e pede informações sobre a geometria da elipse. Vamos lembrar das fórmulas que relacionam esses valores:
Temos as distâncias máxima e mínima do satélite em relação à superfície da Terra. Se somarmos o raio da Terra a esses valores, vamos ter e :
Agora o primeiro par de equações vira um sistema, tal que:

Passo 3
Belejóia, agora temos um sistema de duas equações e duas incógnitas. Podemos usar ele pra resolver a questão toda! Primeiro, vamos achar o valor de .
Somando as duas equações:
Logo:
Ou em :
E assim temos a resposta do item (a)

Passo 4
Agora queremos achar o valor de . Mas como já sabemos que é só a gente substituir isso em qualquer uma das equações. Vamos pegar a primeira:
Logo:
Prontinho!

Resposta
(a)
(b)