Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 13.Problemas Adicionais - Ex. 79
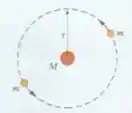
Um sistema de três estrelas é formado por duas estrelas de massa girando na mesma órbita circular de raio em torno de uma estrela central de massa (veja a figura). As duas estrelas em órbita estão sempre em extremidades opostas de um diâmetro da órbita. Escreva uma expressão para o período de revolução das estrelas.
Passo 1
Vamos entender o que está acontecendo aqui. Pode parecer que as duas estrelas de massa estão orbitando a estrela sem sequer notar a existência uma da outra. Mas não é bem assim.
Na verdade, todas as estrelas estão orbitando o centro de massa do sistema. Mas a estrela é tão mais pesada, que o centro de massa fica muito próximo do centro dela!
Ou seja, temos que considerar todo mundo na nossa conta. As leis de Kepler, por exemplo, não podem ser aplicadas diretamente aqui.
Passo 2
Pense em uma dessas esferas menores, de massa , qual é a força que atua sobre elas?
Primeiro temos a força exercida pela estrela :
E agora a força exercida pela outra estrela , que está sempre na outra extremidade, e portanto a distância é simplesmente o dobro do raio (diâmetro da órbita):
Beleza, agora podemos somar as duas:
Passo 3
Continue pensando na estrela de massa , essa força que calculamos mantém ela numa órbita circular, certo? Então podemos dizer o seguinte:
Que é a fórmula da força centrípeta.
Vamos isolar a velocidade:
Agora é só relacionar a velocidade ao período pela fórmula que conhecemos:
Isolando o período:
Pronto! Achamos a fórmula que o enunciado pediu.
Resposta
A fórmula é .