Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 33.Problemas - Ex. 55
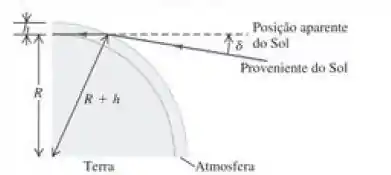
Quando o Sol nasce ou se põe, ele parece estar no horizonte, porém, na realidade ele está abaixo do horizonte. A explicação para esse aparente paradoxo é que a luz se encurva ligeiramente quando penetra na atmosfera terrestre, como indicado na Figura 33.53. Como temos a percepção de que a luz se propaga sempre em linha reta, intuímos que ela provenha de um ponto situado em uma posição aparente que forma um ângulo acima da posição real do Sol. a) Suponha. para simplificar, que a atmosfera tenha uma densidade uniforme e, portanto, um indice de refração constante, e que ela se estenda até uma altura acima da superficie terrestre, onde se interrompe abruptamente. Mostre que o ângulo é dado por
onde é o raio da Terra. b) Calcule usando e . Como esse resultado se compara com o raio angular do Sol, que é aproximadamente igual a um quarto de grau? (Na verdade, um raio de luz do Sol encurva-se gradualmente, e não abruptamente, visto que o índice de refração da atmosfera varia gradualmente com a altura.)
Passo 1
Vamos desenhar o caminho que um raio faz para entrar na atmosfera e vamos marcar alguns ângulos importantes.
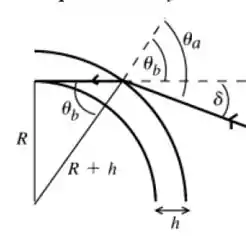
Vamos aplicar a lei de snell na interface vácuo-atmosfera.
Olhando para a figura, percebemos que:
Então:
Pela figura, também vemos que:
Show!!
Bora pra próxima!
Passo 2
b)
vamos substituir os valores que o enunciado deu:
Então
Como de grau corresponde à , temos que corresponde a, aproximadamente, ao raio angular do Sol.
Resposta
a)demonstração
b)